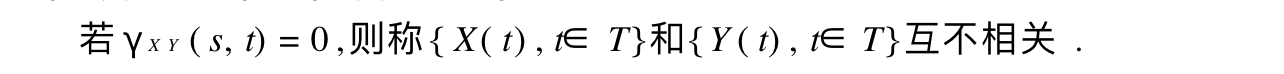Stochastic Process

Stochastic Process course note.

1. stochastic process

1.1. classes of process

• Def: stochastic process

  

  Note:

  

  

1.1.1. stationary

• Def: stationary process

  

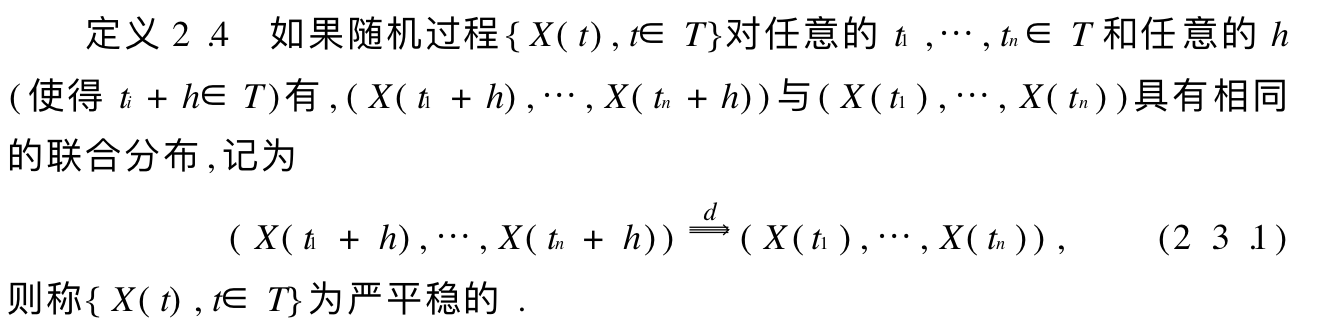
  Note:

  

• Def: broad stationary process

  

  Note:

  

  

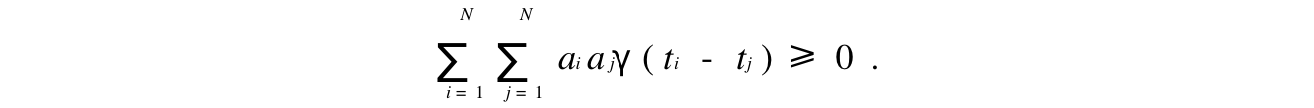
1.1.2. ergodic

• Intro:

  

  Def: ergodic process

  

  

  Note:

  

  • Qua: necc & suff

    

  • Qua: equation =>

    

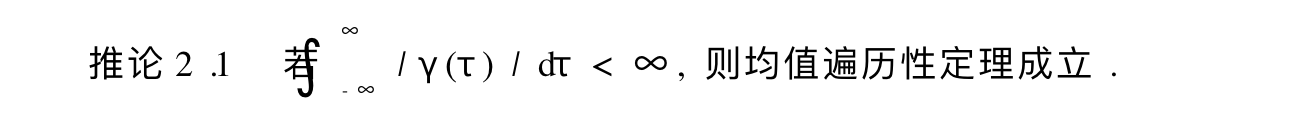
  • Qua: equation =>

    

  • Qua: necc &suff for variance function

    

1.1.3. independent increment

• Def:independent increment process

  

  Note:

  

1.1.4. markov

• Def: markov

  

  Note:

  

  Note:

  

  

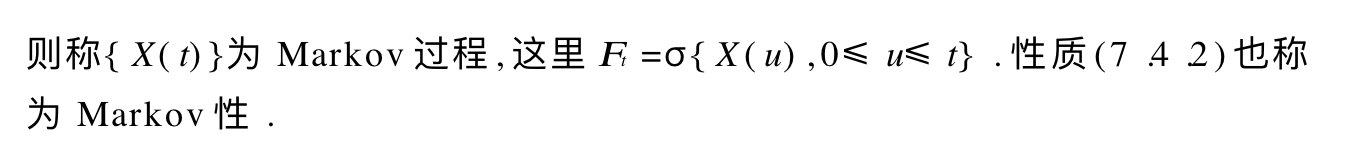
  Note:

  

  

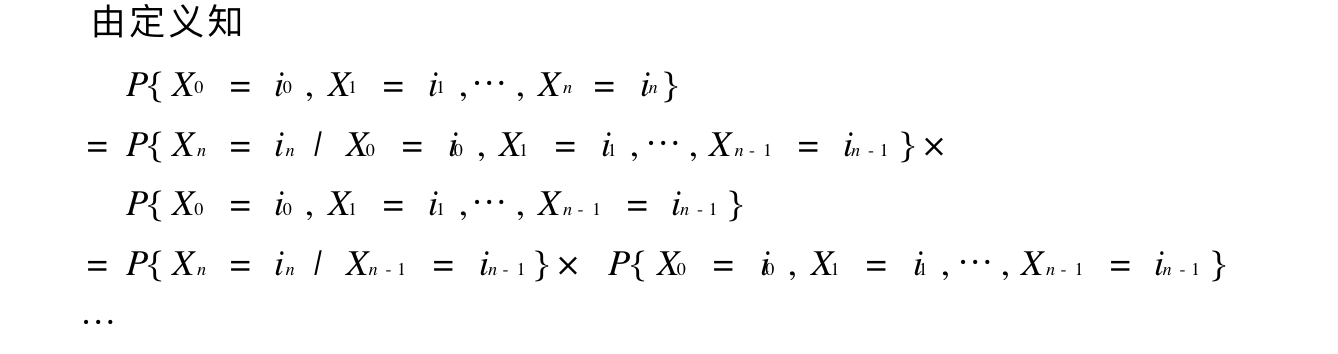
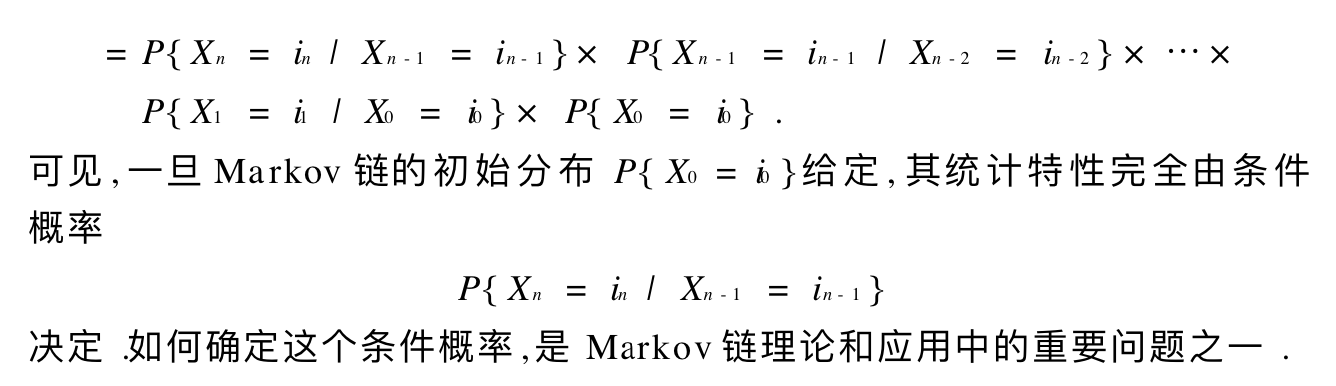
1.1.4.1. inhomogeneous markov

• Def: inhomogeneous markov

  

• Def: trans prob \(p _{ij}\)

  

• Def: n trans prob \(p_{ij}^{n}\)

  

  • Theorem: relationship with pij

    

  • Theorem: relationship with fij

    

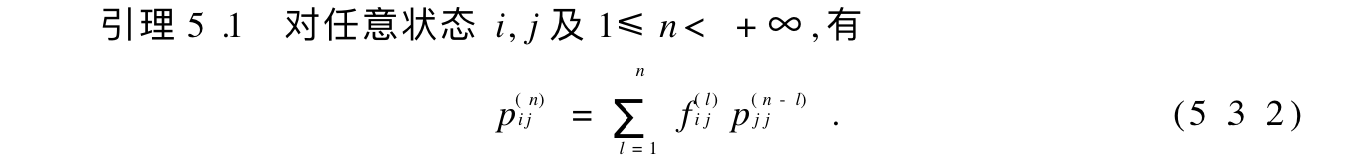
• Def: prob matrix

  

1.1.4.2. reducible markov

• Def: reducible markov

  

• Def: property of status: same class

  

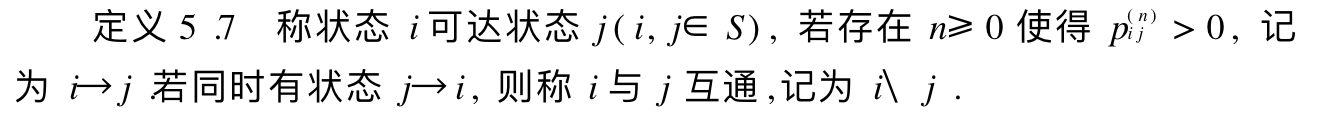
  Note:

  

  • Qua: necc & suff

    

• Def: property of status: circular

  

  Note:

  

  • Qua: same status=>

    

• Def: property of status: Recurrence

  

  Note:

  

  

  • Def:

    

  • Qua: necc & suff

    

  • Qua; => fji

    

  • Qua:

    

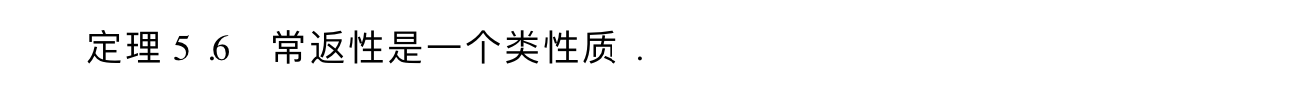
  • Theorem: =>decomposition

    

  • Theorem: => decomposition 2

    

1.1.4.3. limit markov

• Def: limit markov

  

• Theorem:

  

  Note:

  

  • Corollary:

    

• Theorem:

  

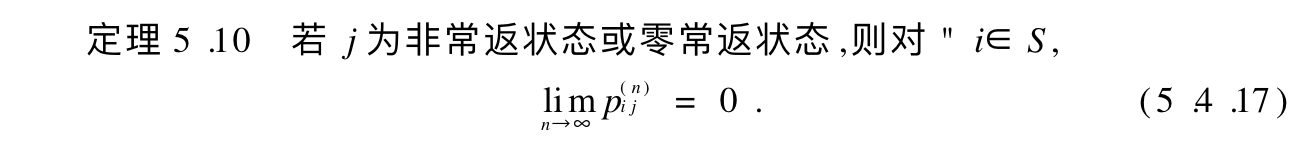
  • Corollary:

    

  • Corollary:

    

• Theorem:

  

  

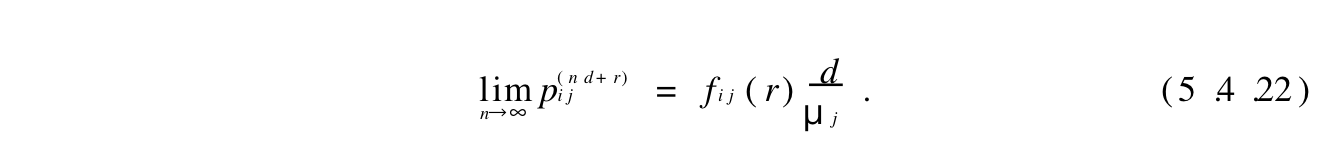
  • Corollary:

    

• Lemma:

  

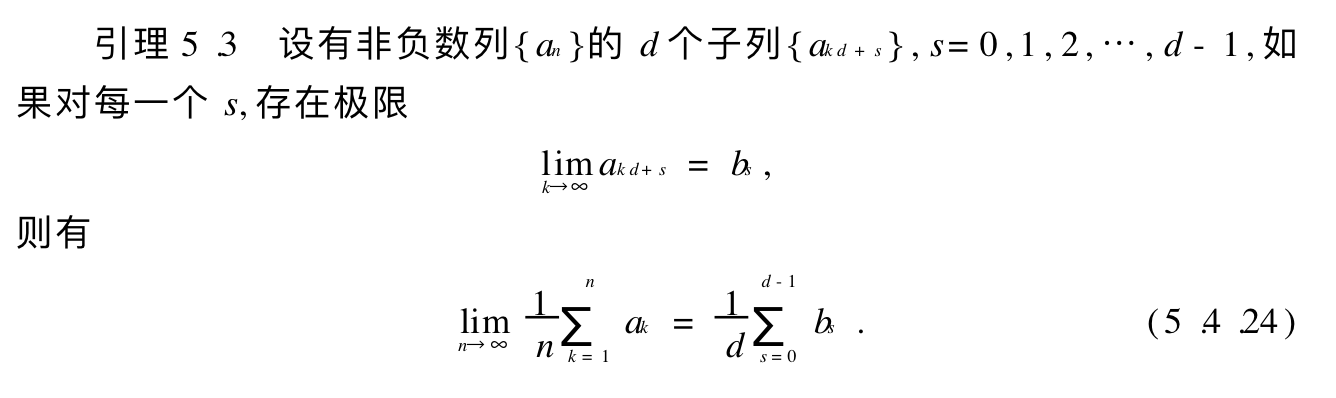
  Theorem:

  

  • Corollary:

    

    Note;

    

1.1.4.4. unchanged markov

• Def: unchanged markov

  

  • Theorem: => relationship

    

• Def: large number p109

1.1.4.5. continuous markov

• Def: continuous markov

  

  Note:

  

  • Qua: => distribution

    

    Note:

    

• Def: regularized markov

  

  

• Theorem:

  

• Theorem:

  

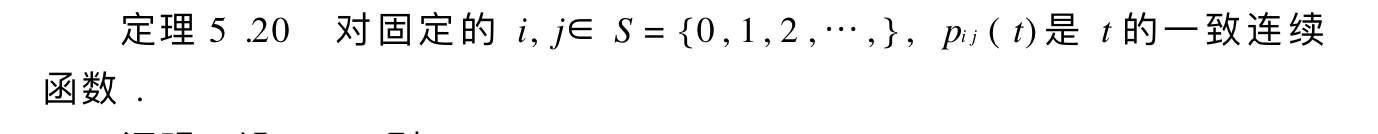
• Theorem:

  

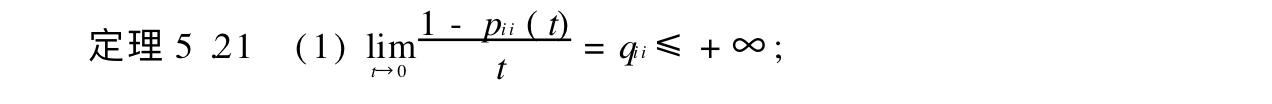
  • Corollary:

    

    Note:

    

• Theorem:

  

• Def: the final

  

1.1.4.6. strong markov

• Def: time stop

  

  Note:

  

  

• Def: strong markov

  

1.1.4.7. examples: population

1.1.5. Levy

• Def

  

• Def:

  

• Def:

  

  

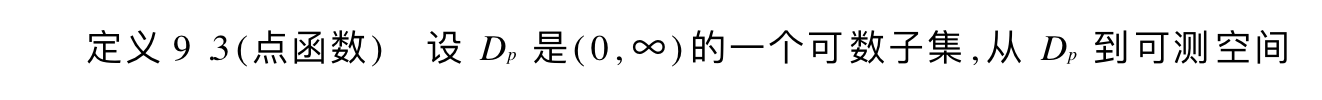
• Def;

  

• Def:

  

  

• Def:

  

• Def;

  

  

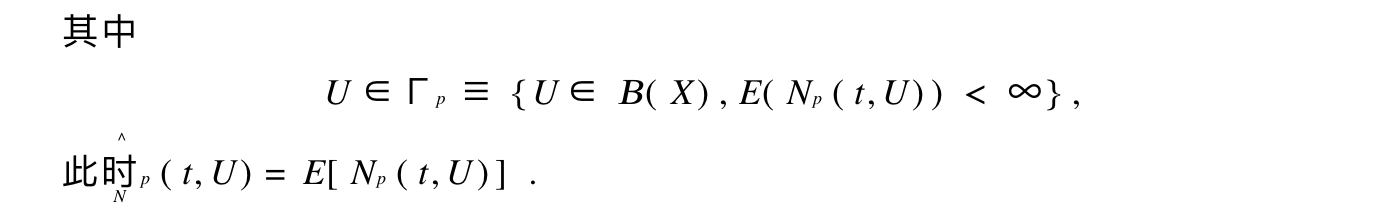
• Def:

  

• Theorem:

  

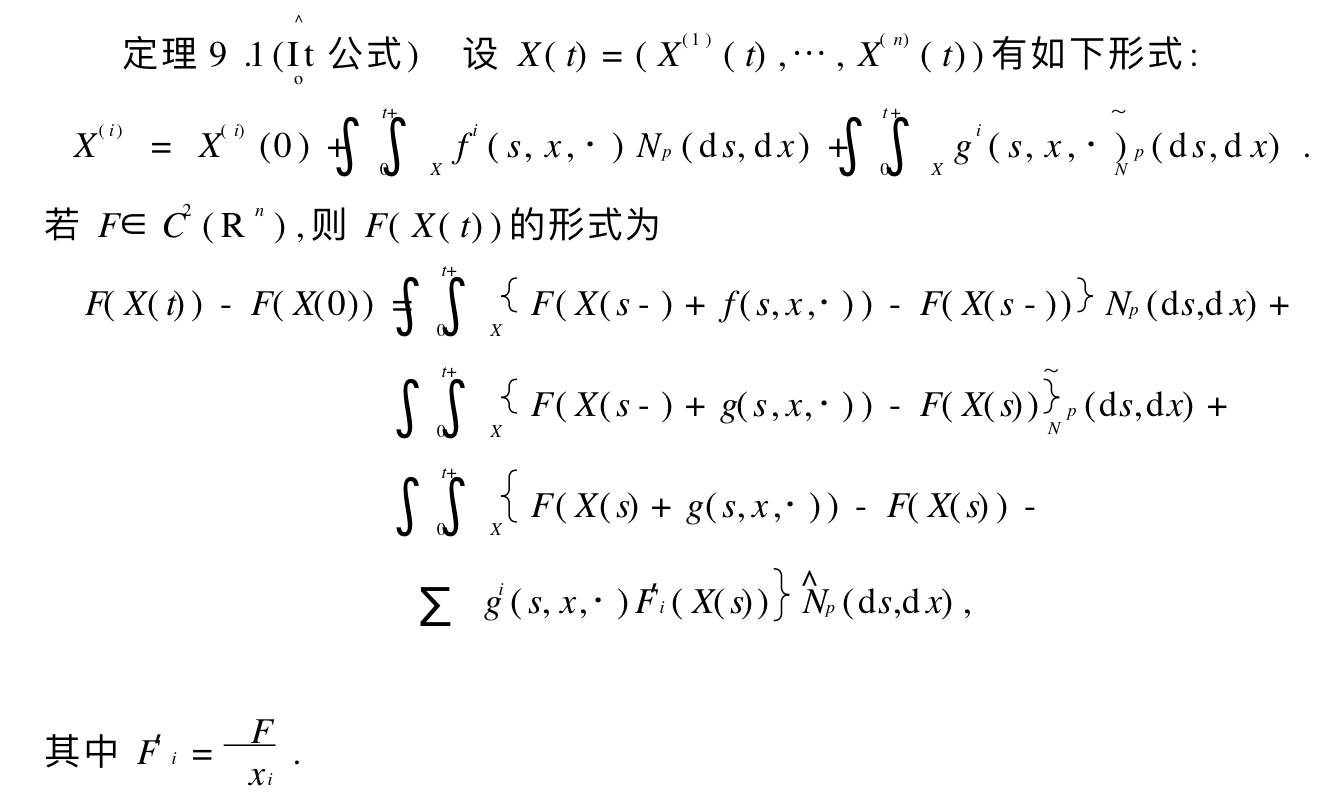
1.2. distribution

• Def: finite joint distribution

  

  • Qua: => some qualities

    

  • Qua: kolmogov => exist

    

    Note:

    

1.3. special function

1.3.1. expectation

• Def: expectation & 2 moment process

  

  

  • Qua: => that co-var & autocorrelation exist

    

1.3.2. variance

• Def: variance

  

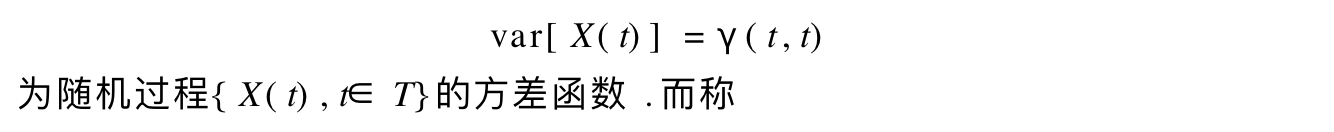
1.3.3. co-variance

• Def: co-variance

  

1.3.4. autocorrelation

• Def: autocorrelation

  

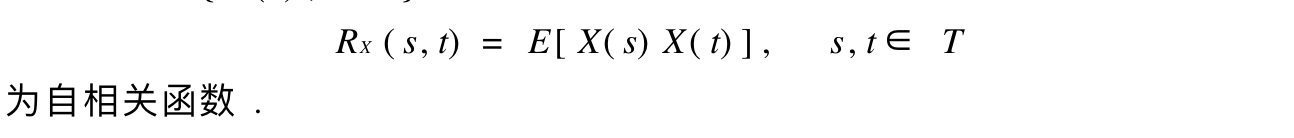
1.4. integration

• Def:

  

  • Qua: =>

    

• Def:

  

1.4.1. It integral

• Def:

  

  • Theorem:

    

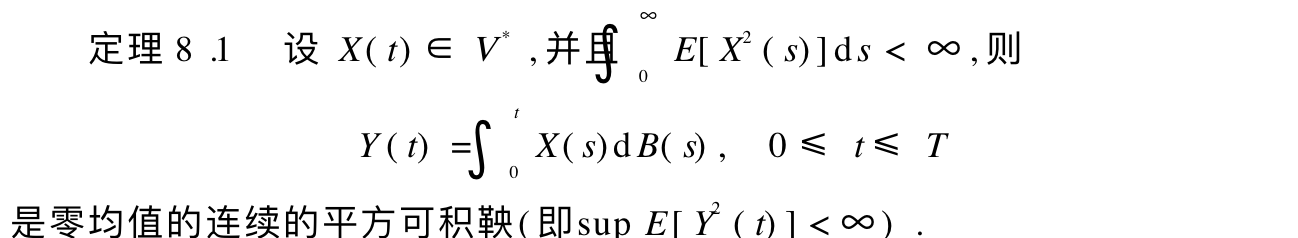
    • Corollary:

      

  • Theorem:

    

• Def:

  

  

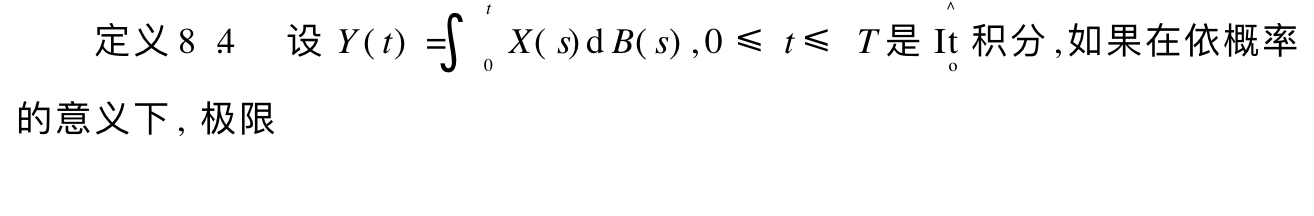
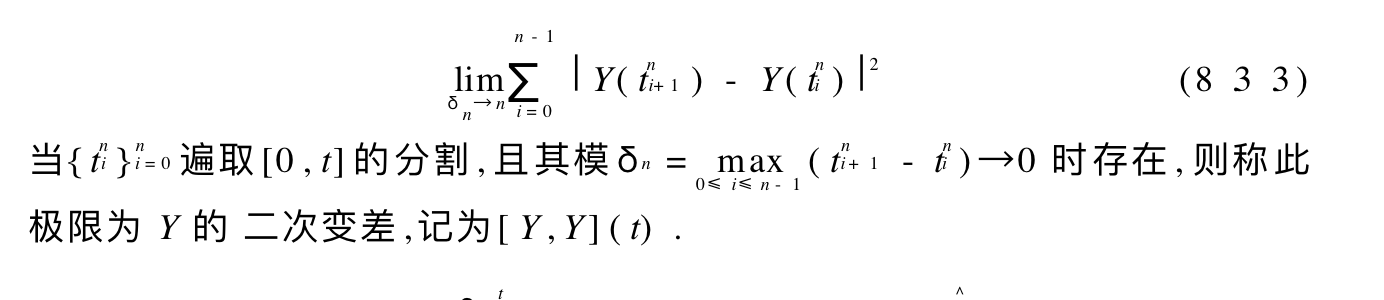
  • Theorem:

    

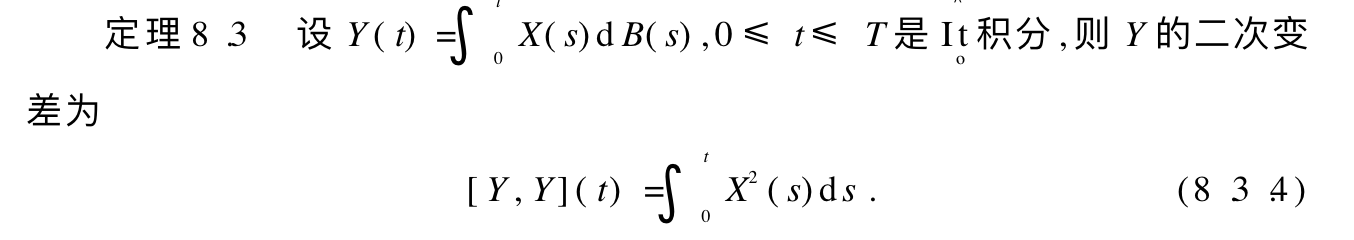
1.4.2. It process

• Theorem:

  

  

• Theorem:

  

• Def:

  

• Theorem:

  

2. useful processes

2.1. poisson

• Def: counting process

  

• Def: poisson process

  

  

  

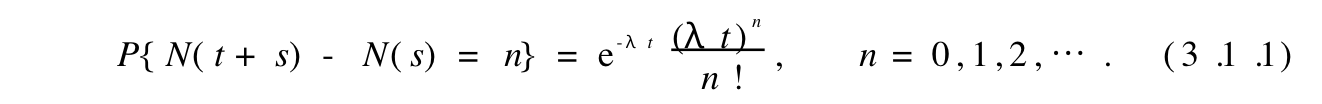
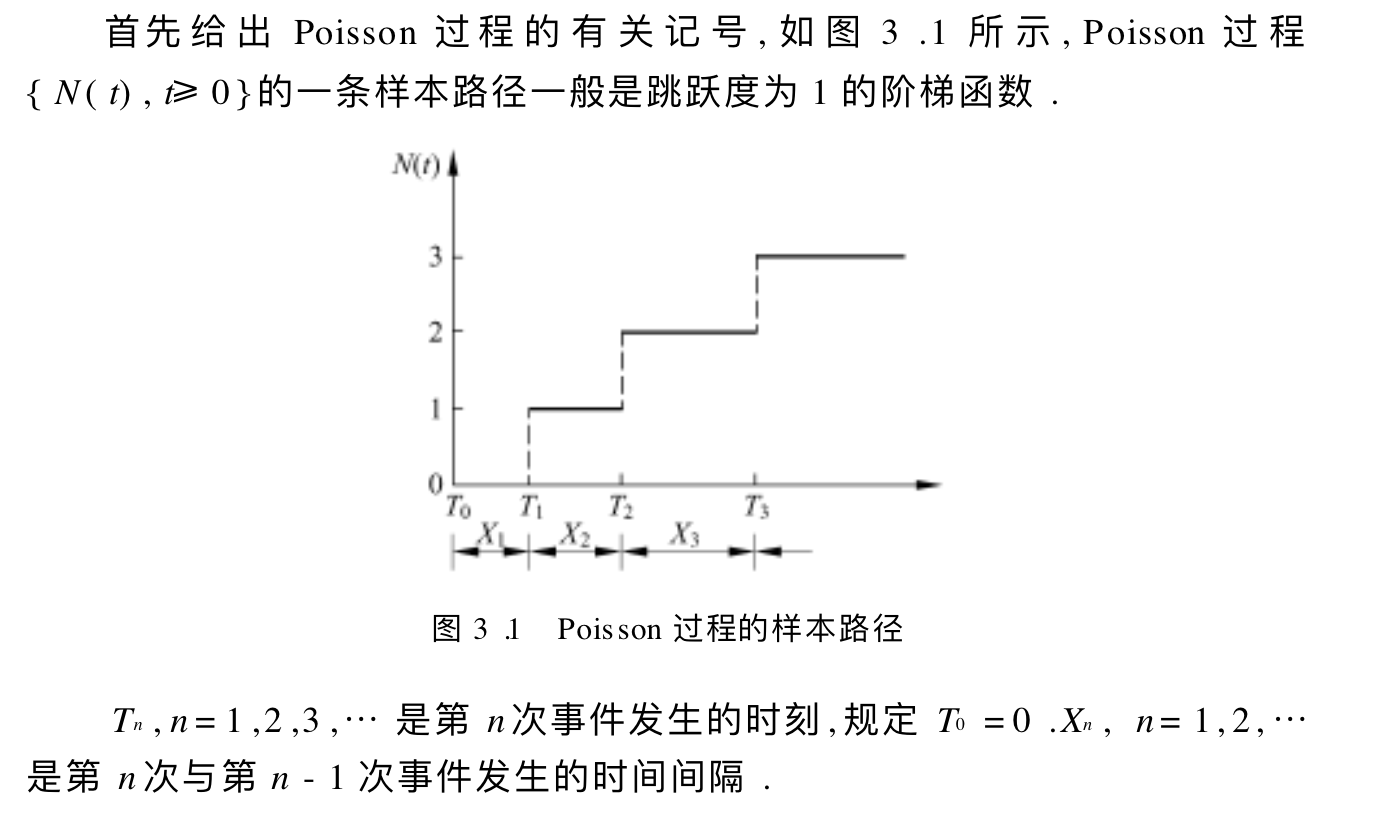
  Note:

  

  • Qua: necc & suff

    

    

  • Qua: necc & suff

    

  • Qua: Xn distribution =>

    

    Note:

    

  • Qua: tn distribution =>

    

  • Qua: tn conditional distribution =>

    

2.1.1. inhomogeneous poisson

• Def; inhomogeneous possion

  

  

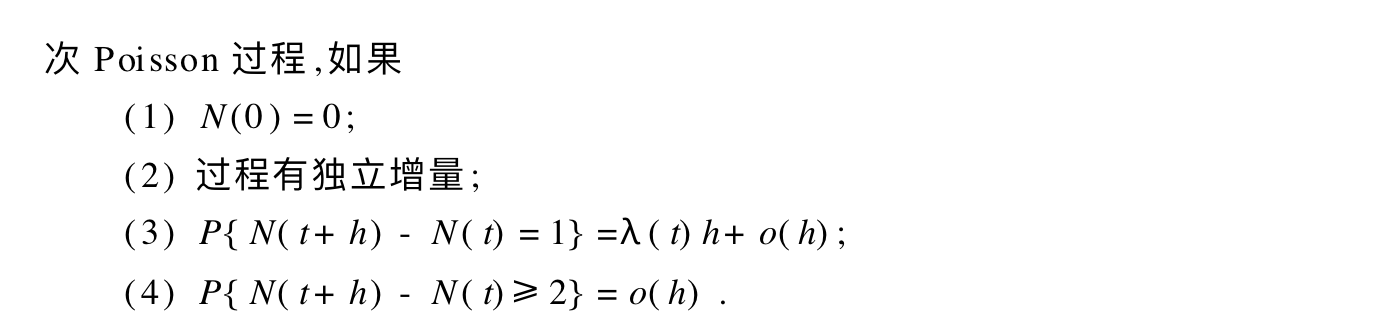
  • Qua: necc & suff

    

  • Qua: transition with normal =>

    

    Note:

    

2.1.2. complex poisson

• Def: complex poisson

  

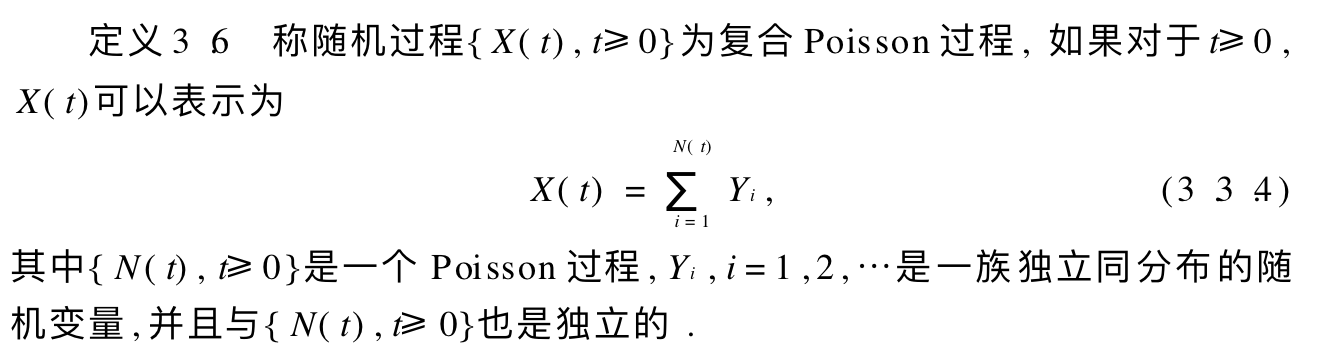
  Note:

  

  • Qua: => property

    

    

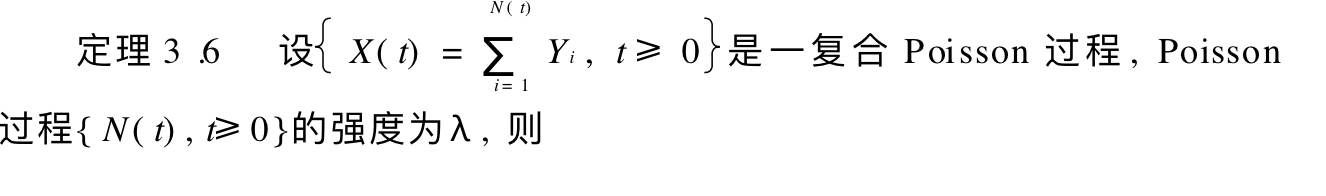
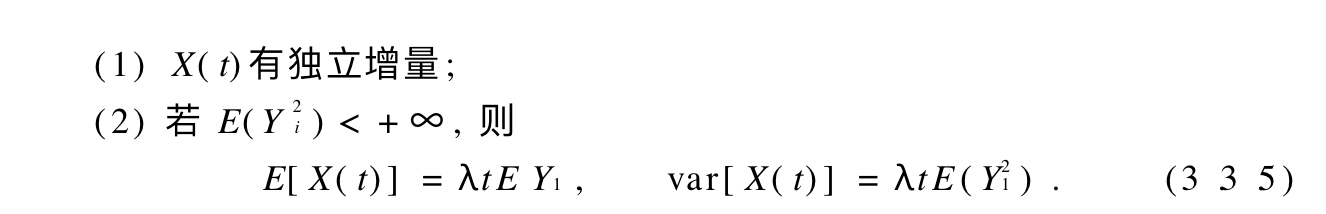
2.1.3. condition poisson

• Def; condition poisson

  

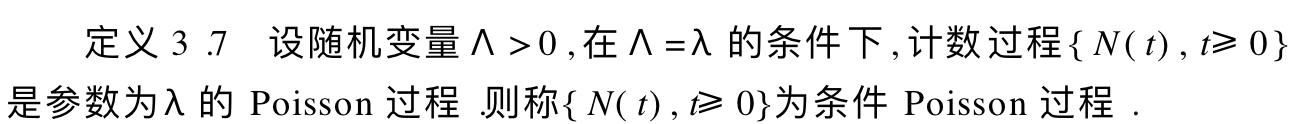
  Note:

  

  • Qua; => e & var

    

2.2. brown

• Def:

  

  • Qua: necc & suff

    

    Note:

    

• Def: inhomo brown

  

• Def:

  

  • Qua: =>

    

  • Qua: =>

    

2.2.1. martingale

• Theorem:

  

  Note:

  

2.2.2. markov

• Theorem:

  

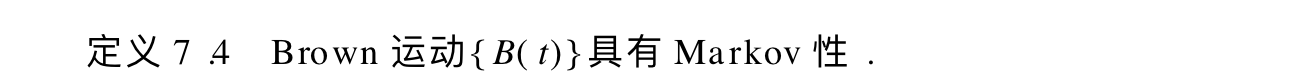
• Def:

  

• Theorem: strong markov

  

2.2.3. maximum

• Def:

  

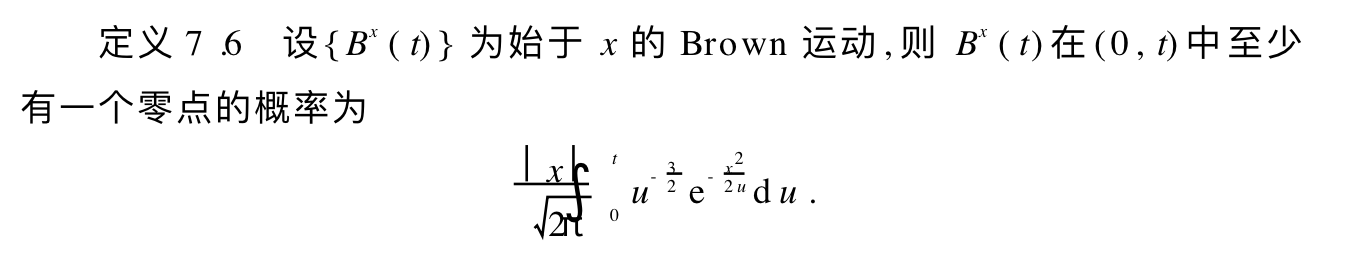
2.2.4. generlization

2.2.4.1. brown bridge

• Def:

  

2.2.4.2. efficient absorb brown

p173

2.2.4.3. reflected brown

• Def:

  

2.2.4.4. geometry brown

• Def:

  

2.2.4.5. shifted brown

p 180

2.3. Gauss

• Def: gauss process

  

3. relationship of stochastic process

## special function

3.0.1. cross-covariance

• Def: cross-covariance

  

3.1. correlation

• Def: correlation