Measure Theory Class Notes
1. $ F , P$
1.1. collection of sets \(F\)
Def: subset of power set: algebras
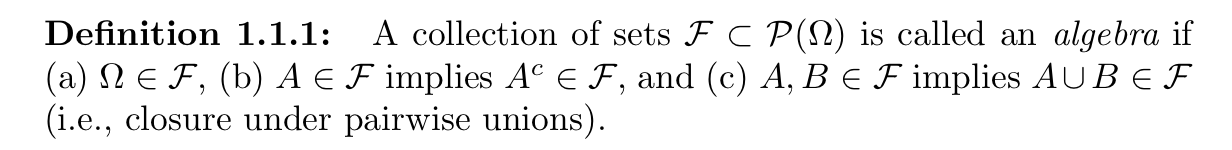
Def: subset of power set: \(\sigma\)-algebra
Usage: a subset of power set + closed under countable unions
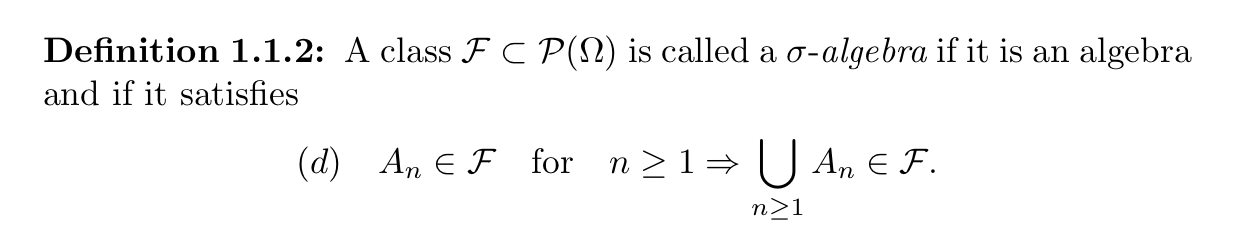
Example:
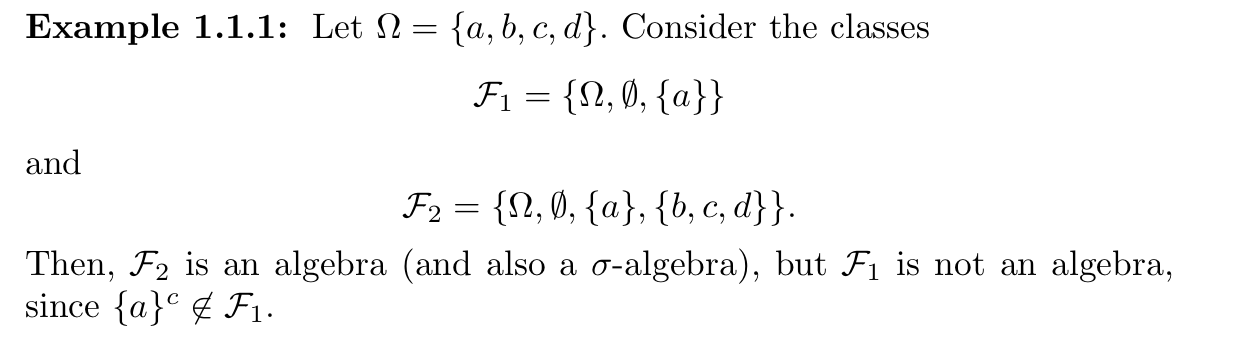
Qua: necc& suff

Def: subset of power set: \(\sigma\) - algebra generation by subset
Usage: a subset of power set: the smallest \(\sigma\)- algebra contains this subset.
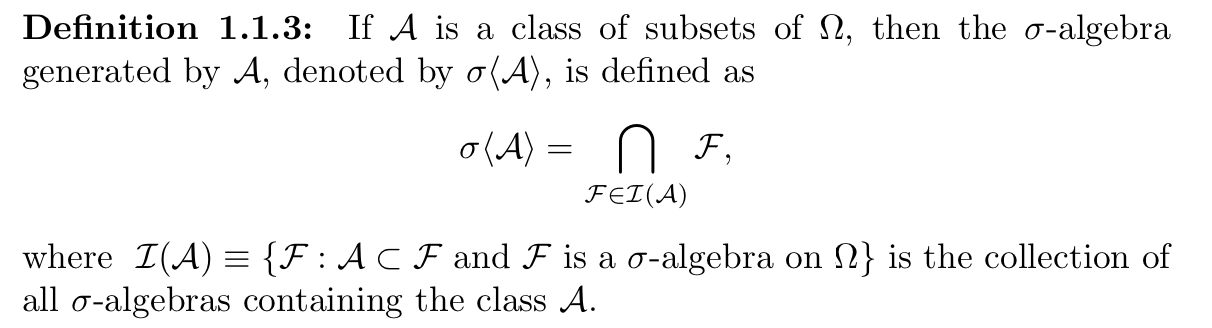
Def: subset of power set: \(\sigma\) - algebra generation by collection of open sets in S.

Def: subset of power set: \(\pi\) -system
Usage: class of subset of \(\Omega\)
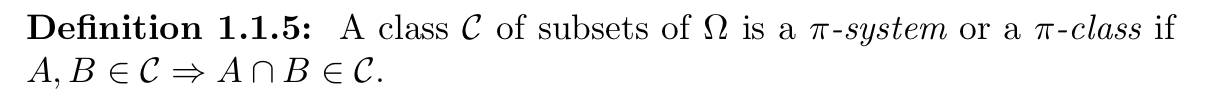
Def: subset of power set: \(\lambda\)- system
Usage: class of subset of \(\Omega\)
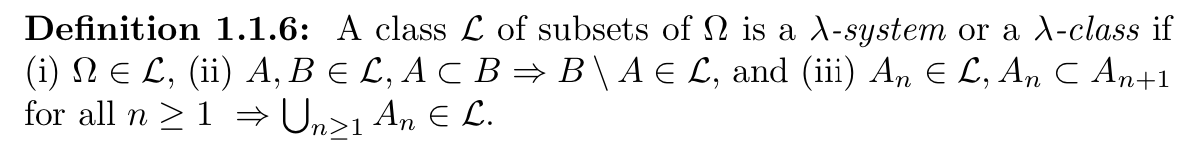
Qua: \(\sigma\) - algebra =>
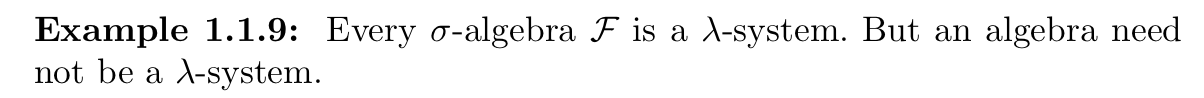
Qua: L1 + L2 =>

Qua: the \(\pi,\lambda\) theorem
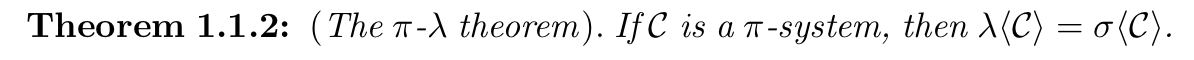
Corollary:

1.2. set function (measure) \(P\)
Def: set function \((F \to R)\): are defined on a class of subsets of a set \(\Omega\)

Note:

Qua: necc & suff

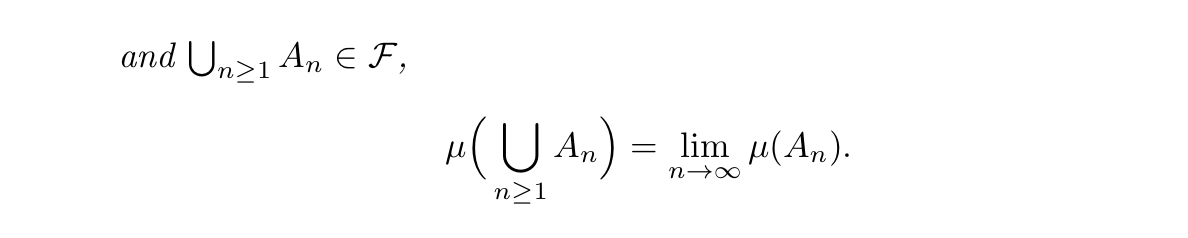
Qua: => the three qualities of measure
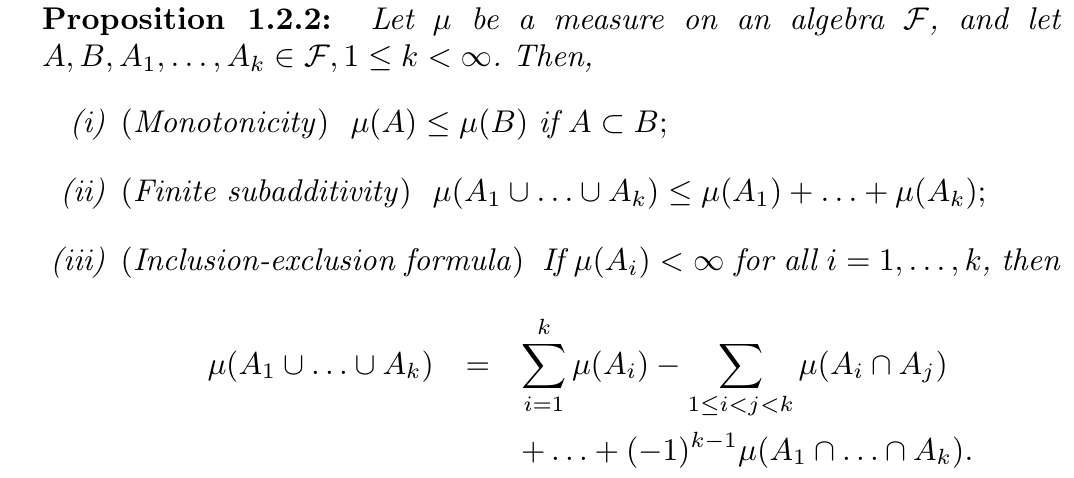
Note: lead to prop below

Qua: => to \(\infty\)
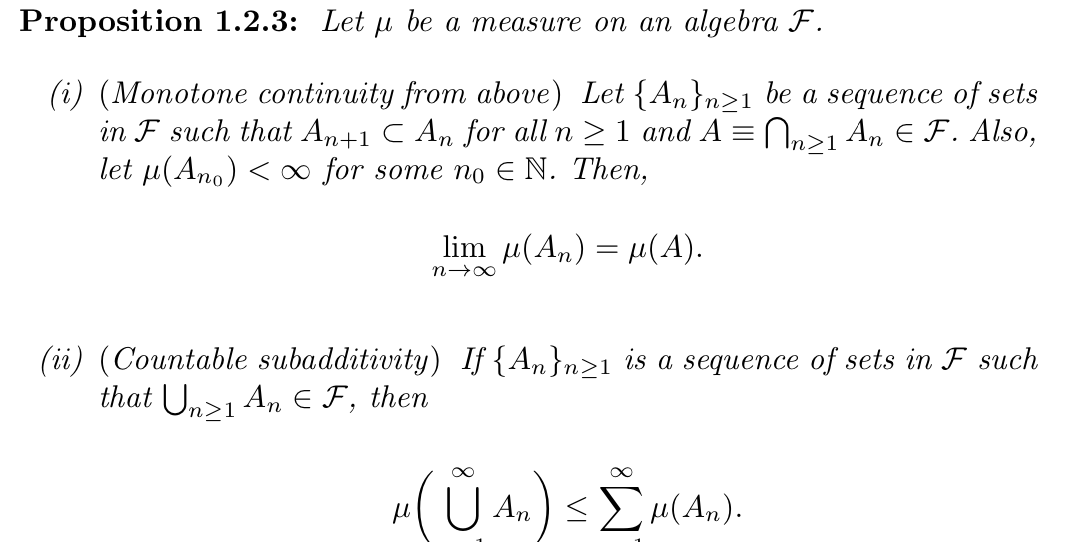
Qua: => uniqueness of measure
Note: that measure is unique if every \(\mu\)(\(\pi\)- system) yield the same result.

Def: set function: finite measure/ probability space/ \(\sigma\)-finite

Example:

1.3. extension theorem
1.3.1. Caratheodory extension of measures \(P\)
Def: redefine measure
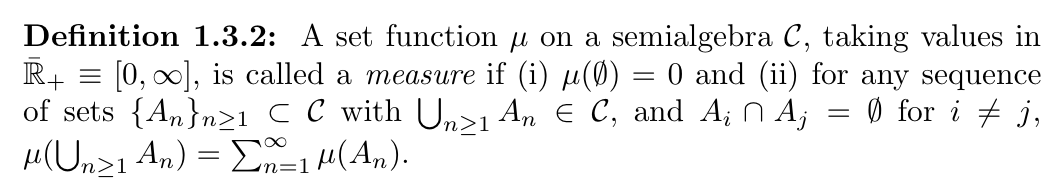
Def: a subset of power set: semialgebra

Qua: => this problem

Def: set function \((F \to R)\): outer measure induced by $ $

Note: equavalent definition

Note:

Qua: => `yield a
Usage: yield a measure space on \(\Omega\)

Def: set: \(\mu^*\)- measurable
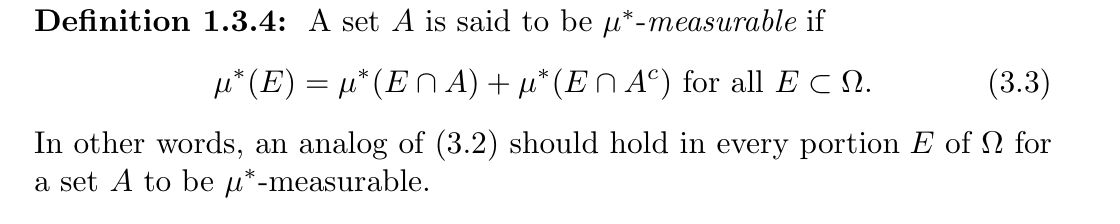
Def: complete measure space

Theorem: the final theorem

1.3.2. Lebesgue measure on R \(P\)
Intro:

Def: measure space \(\left(\mathbb{R}, \mathcal{M}_{\mu_{F}^{*}}, \mu_{F}^{*}\right)\)

Def: set function P: Lebesgure measure

Qua:


1.3.3. Lebesgure measure on $ R^2 $ P
2. \((\Omega, F,P)\)
2.1. measurable space \((\Omega, F)\) & measure space \((\Omega ,F,P)\)
Def: measurable space \((\Omega, F)\) & measure space \((\Omega ,F,P)\)

2.2. measurable sample function f
Def: sample function \(( \Omega \to R)\): \(<F,B(R)>\) - measurable
Usage: a random variable is a measurable function


Note: equivalent definition that (1.1) applies to all Borel sets B(R)

Qua: operation
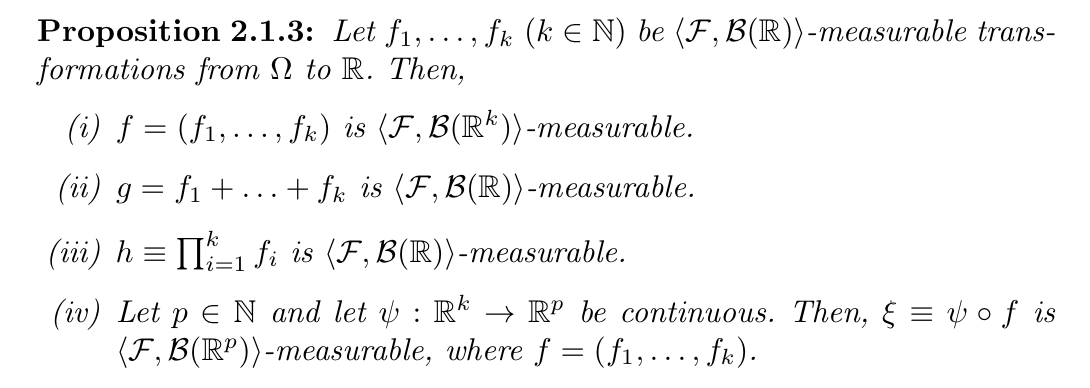
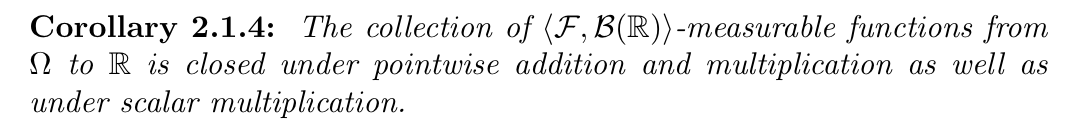
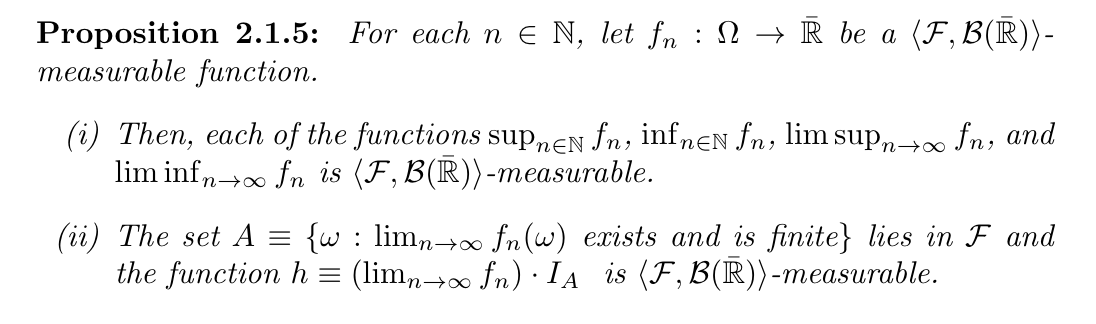
2.3. measuable mapping T
Def: mapping $( _1 _2 ) $: \(<F_1, F_2>\) - measurable

Qua: continuous function =>
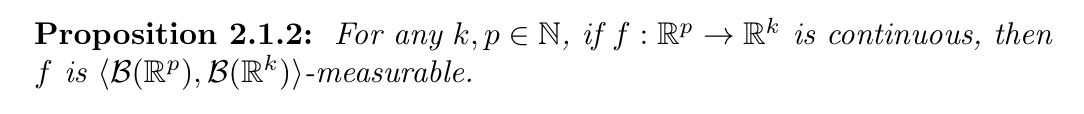
Qua: operation
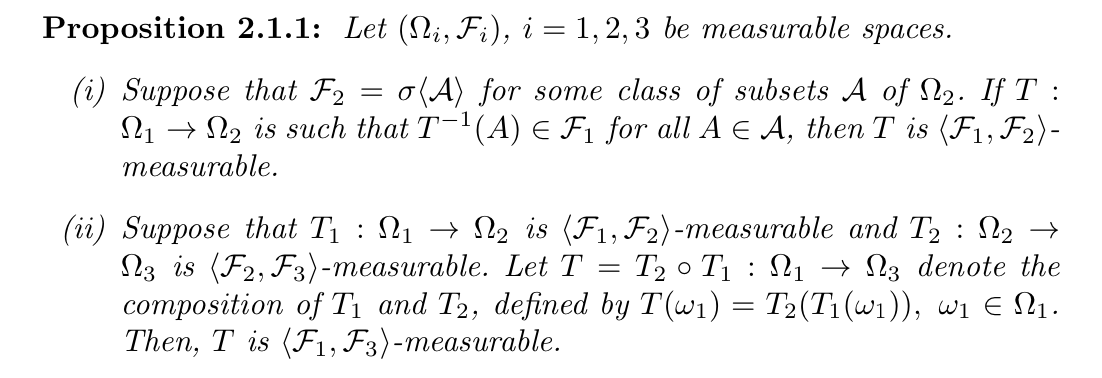
Qua: operation
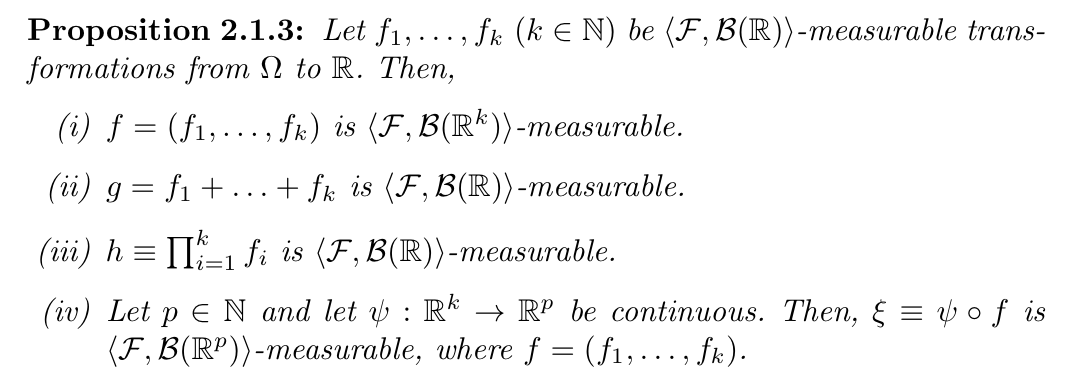
Def: subset of power set: \(\sigma\) - algebra generated by a family of mapping
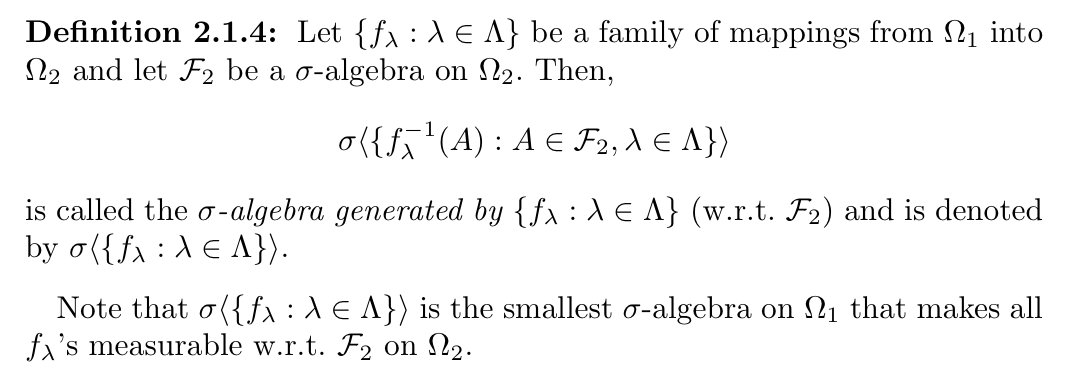
2.4. induced measurable sample function f (distribution functions)
Def: sample function \((\Omega \to R )\): induced by mapping T
Usage: set function(measure) on F2 by inverting to F1 and use measure in F1

Theorem: that P induced by a measurable mapping is still P

2.5. Lebesgue integration
2.5.1. integration of simple function
Def : sample function \(( \Omega \to R)\): simple
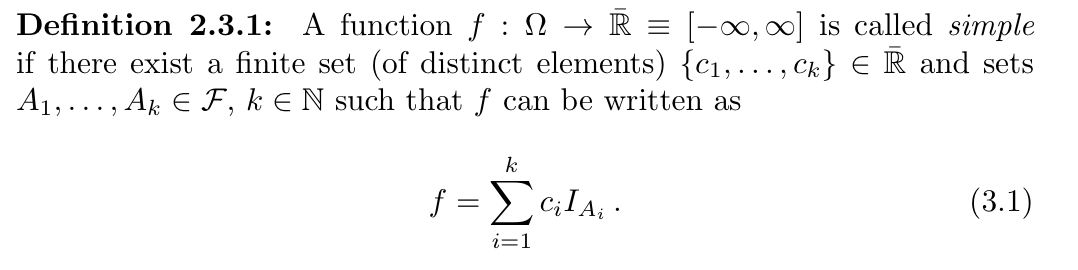
Def: integration of sample function over set function(measure): of simple sample function
Usage: see this as shattering the Riemann intg where you adding the M(subsets) with the same value, it's like a clustering of value, and it can yield benifits that some Riemann intg demands continuous etc, Leb do not.

Note: if not distinct still apply

Qua: => the basic qualies of intg of simple
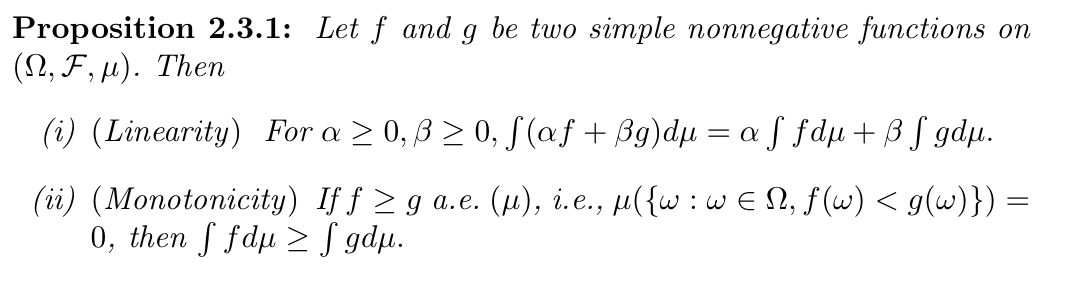
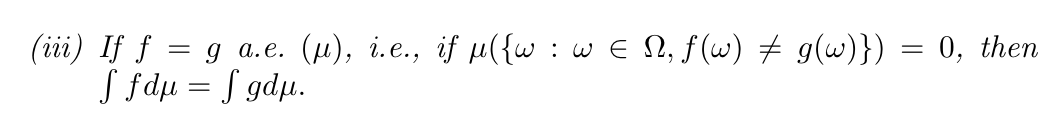
2.5.2. integration of measurable function withn simple functions
Def: integration of sample function over set function(measure): of a limit of simple functions
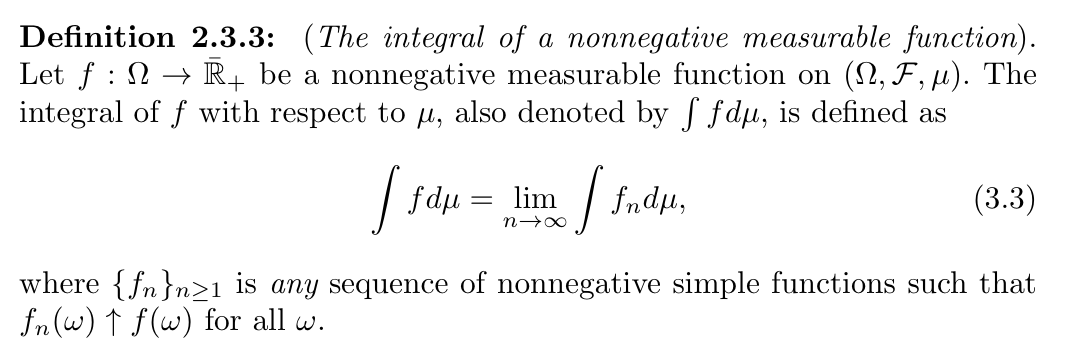
Qua: => uniqueness
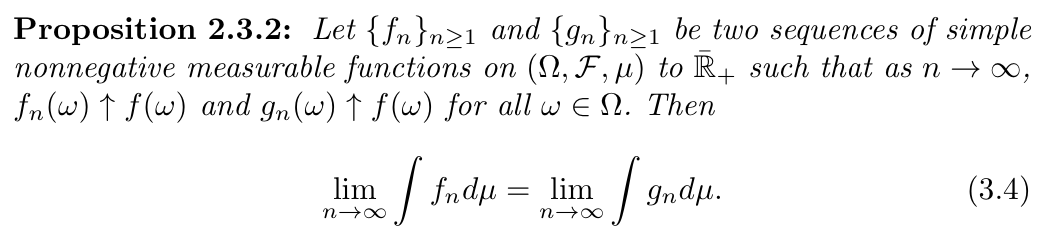
2.5.3. integration of measurable functions (final definition)
Def: another definition not using simple functions
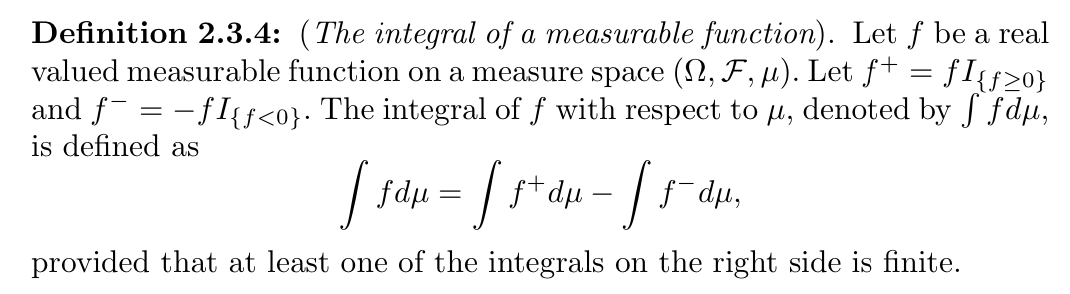
Note: => general measurable function integral (not simple functions)
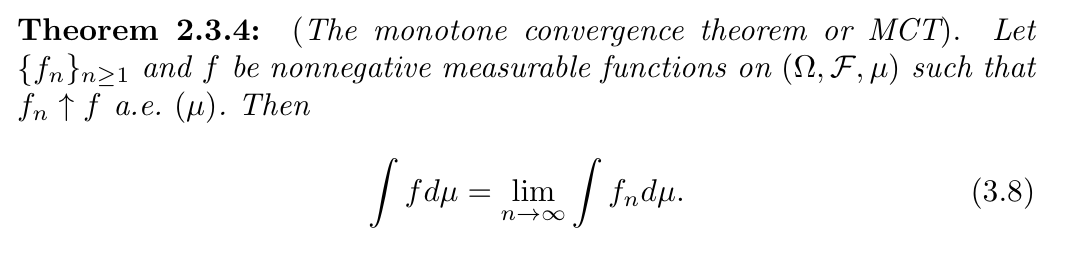
Note:
Qua: => basic qualities still apply

Qua: operation (between sum & integral)
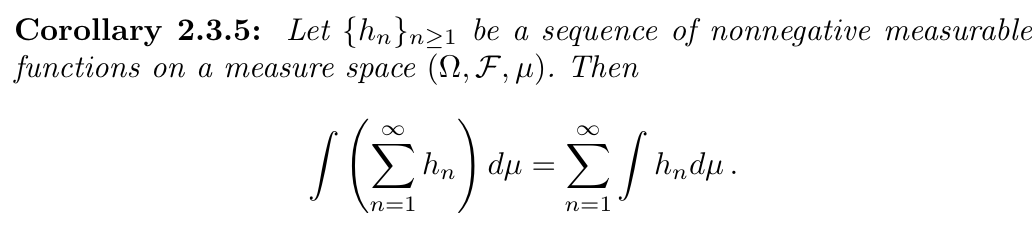
Corollary: we can define a measure on this
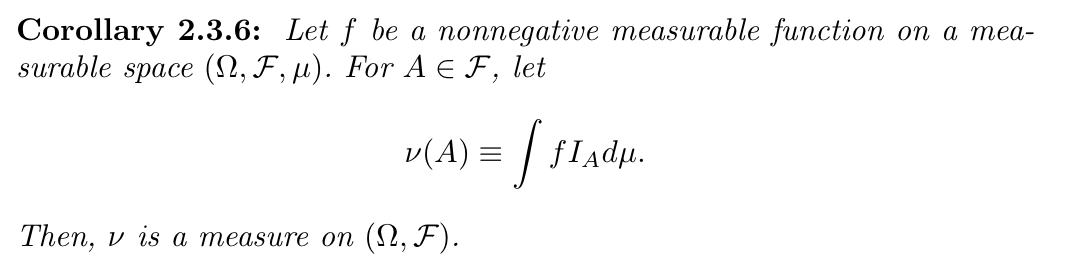
Qua: operation (between limit & integral)
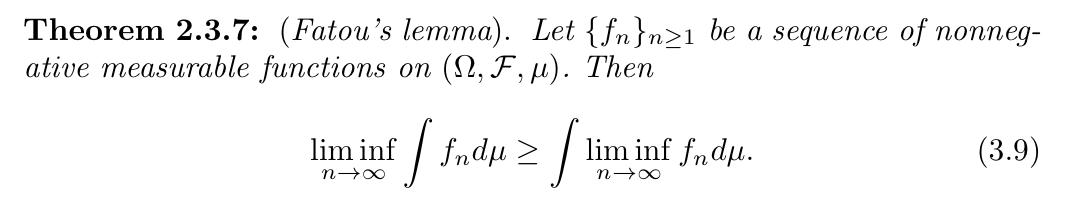
2.5.4. Lebesgue integratable
Def: sample function \((\Omega \to R)\): measurable & integratable function

Note:
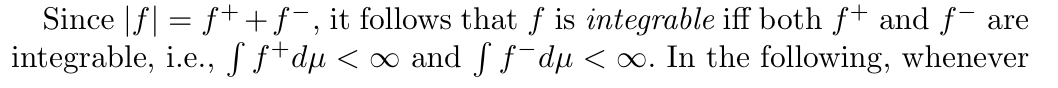
Qua: => qualities
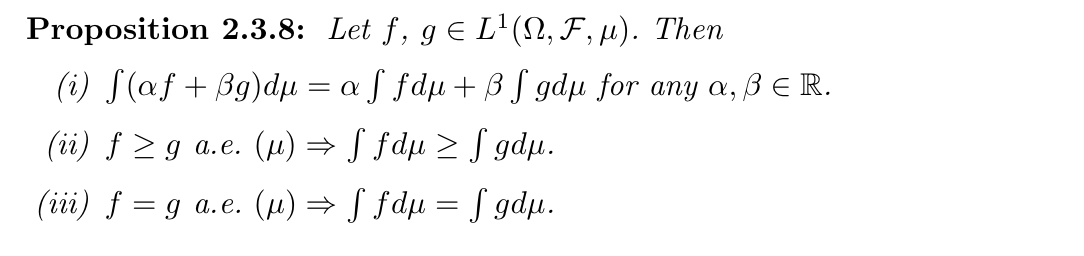
Qua: =>
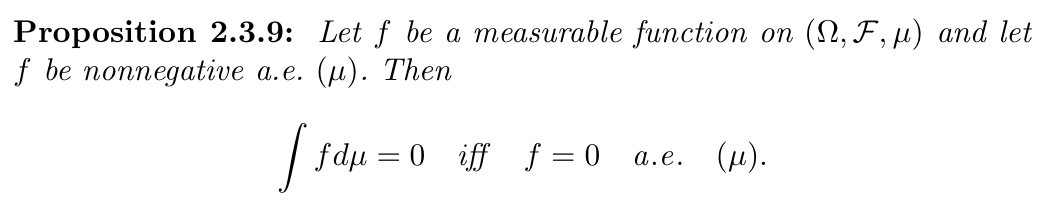
Qua: => l1 space
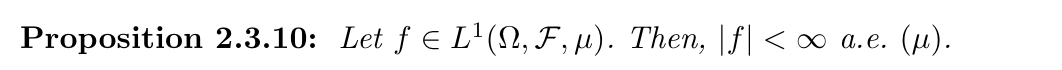
Def: integral over A
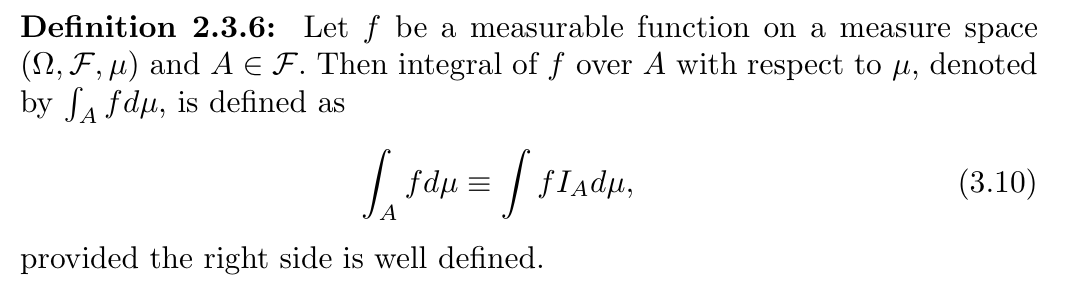
2.5.5. EDCT
Theorem:

Corollary:

Theorem:

2.5.6. Riemann integral
Def: upper/lower sum

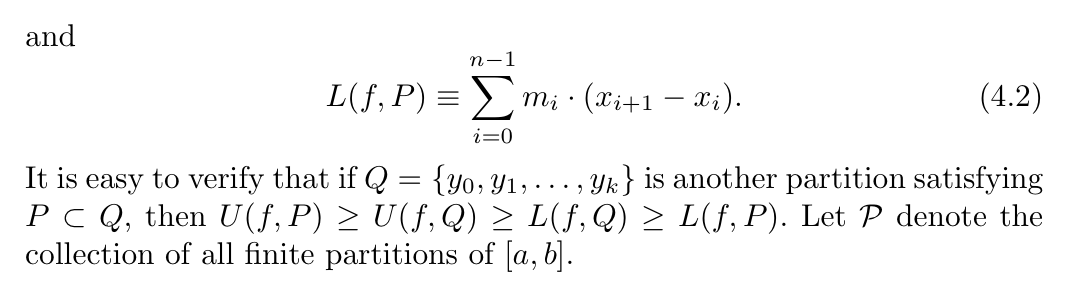
Def: upper/lower Riemann integral

2.5.7. Riemann integrable
Def: Riemann integrable
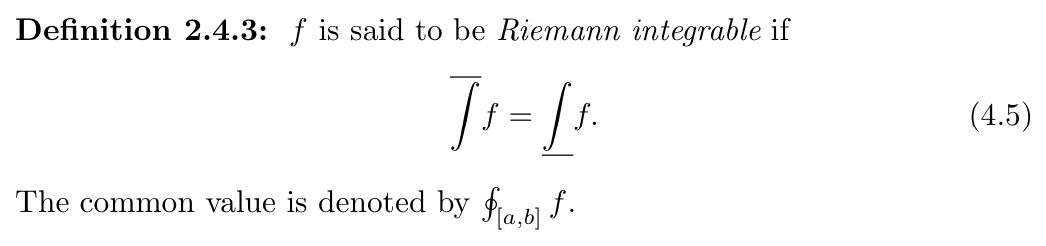
Theorem: relationship with Lebesgue intg

Note:

Note:


