Data structure & Algorithm & Leetcode

Posted on 2019-11-19 | In computer science | total read times

Words count in article: 28.6k | Reading time ≈ 157

Data structures & algorithms & leetcode

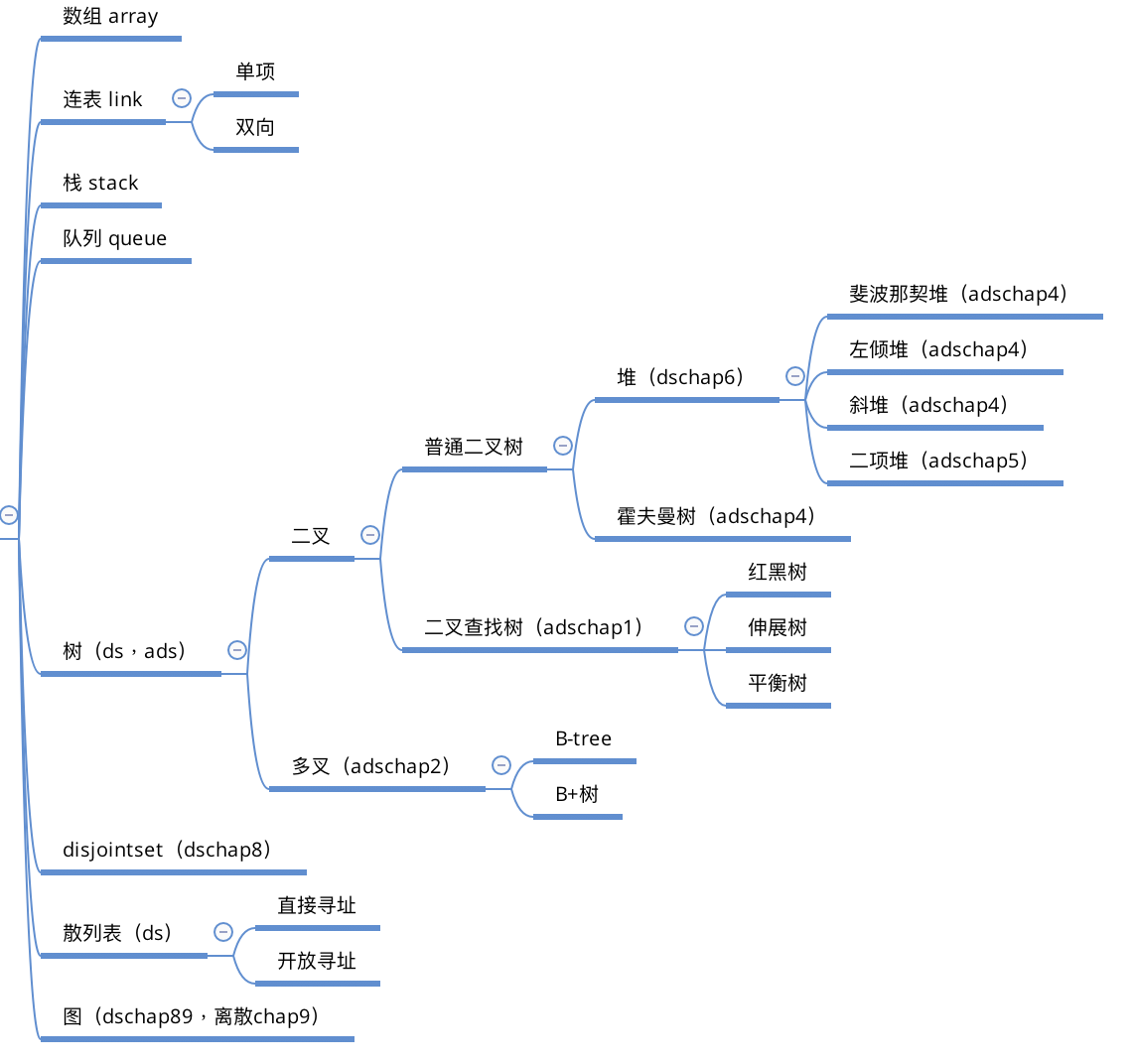
1. data structures

Note: Since most of STL will meet daily need, the following passage will describe basically self-implementation data structrues and analyze their complexities. We use Structure to describe it's intuition, Usage meaning how will it help with real problems, Complexity to analyze it's complexity.
Note: overall picture of data structure
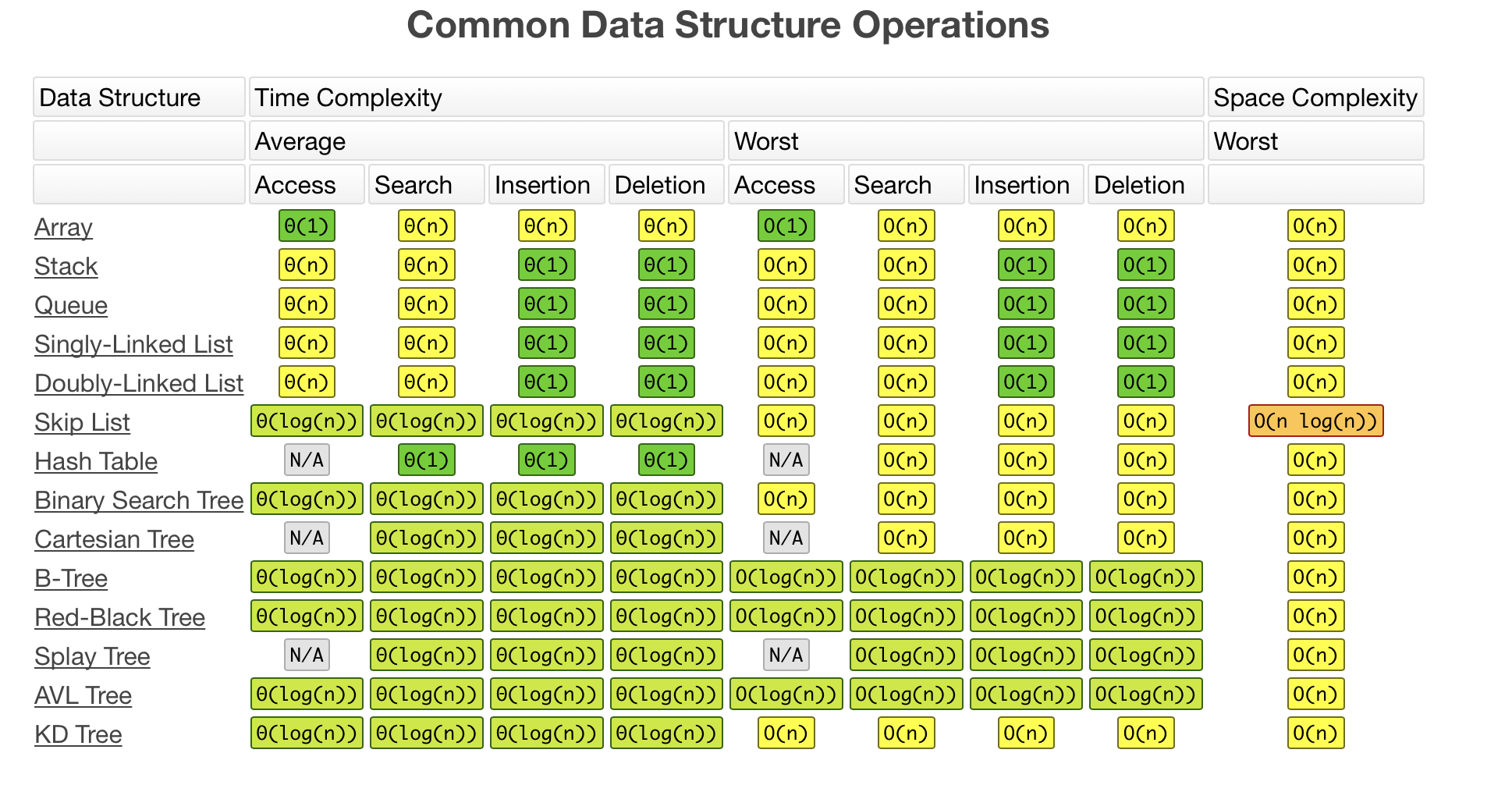
Note: datastructure complexity, set.find() is O(1)
Note: sorting algorithms
Note: STL operations

img

1.1. linear ADT

1.1.1. vector

1.1.2. map

Usage:
- to separate problem/ squeeze searching space(1178)
- to find the next smallerst larger / next largest smaller

1.1.3. stack

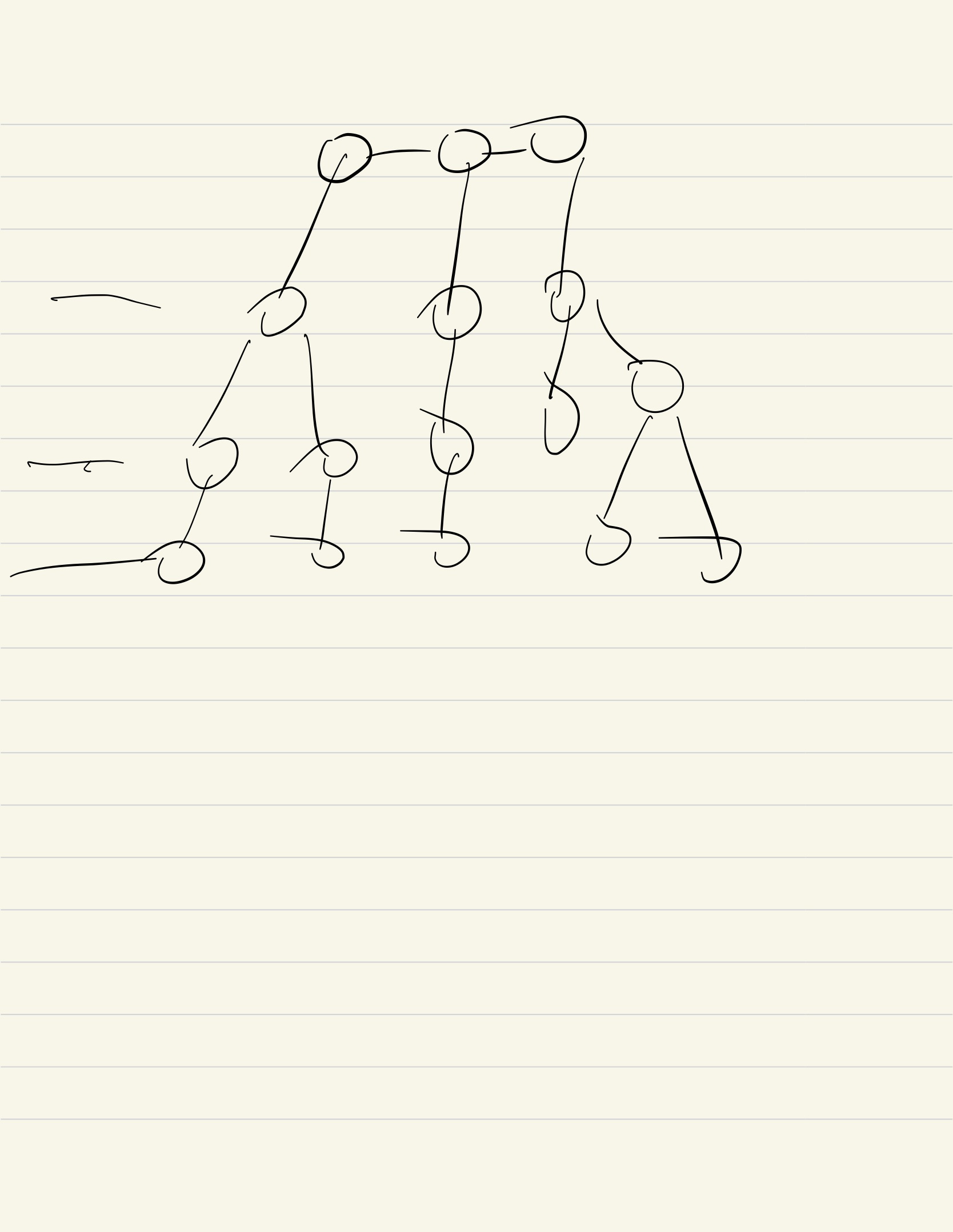
Usage: normally used for keeping a increasing(decreasing just opposite) sequence as well as partial maximum, normally concerned with greedy method
- Smallest element of [1:i]
- Smallest (increasing) number of[1:i]
- Next smallest larger element of ([i]) (decreasing stack)
  - Note: by sorting, and doing PNL on index stack.
- Previous nearest less element of ([i])
  - Note: each step do the following: 1) fixed ith outcome by poping those are larger 2) fixed possible solutions from [1:i] for i+1 and other elements. so keep an array of [possible previous less elements as well as already updated[1:i] ] it is a natually formed increasing array.
- Next nearest less element of ([i])
  - Note: each step do the following: 1)updated some from [1:i-1] outcome by poping those are larger 2) fixed unupdated indexes. The reason why we want to pop elements because 3->7->8->2 we can't reach 3 unless we pop, of course we can record all undecided indexes and move a pointer. And we can find out the problem naturally forms a increasing array (the undecided values), so stack can be used to store these values. It is important to point out that the problem itself forms an increasing array of [ undecided indexed [1:i]], stack is only a easy and natural way to implement it.
- parser
  - Note : make sure starting condition and jumping end condition and while recursive

1.1.4. heap

Usage: heap are great data structure for local max extracting which means greedy algorithms
- extract local min/max
Complexity:
- buildheap = O(n)https://www.cnblogs.com/xcw0754/p/8398535.html

1.1.5. bitset

Usage:

异或的特性。第 136 题，第 268 题，第 389 题，第 421 题，

x ^ 0 = x
x ^ 11111……1111 = ~x
x ^ (~x) = 11111……1111
x ^ x = 0
a ^ b = c  => a ^ c = b  => b ^ c = a (交换律)
a ^ b ^ c = a ^ (b ^ c) = (a ^ b）^ c (结合律)

构造特殊 Mask，将特殊位置放 0 或 1。

1. 将 x 最右边的 n 位清零， x & ( ~0 << n )
2. 获取 x 的第 n 位值(0 或者 1)，(x >> n) & 1
3. 获取 x 的第 n 位的幂值，x & (1 << (n - 1))
4. 仅将第 n 位置为 1，x | (1 << n)
5. 仅将第 n 位置为 0，x & (~(1 << n))
6. 将 x 最高位至第 n 位(含)清零，x & ((1 << n) - 1)
7. 将第 n 位至第 0 位(含)清零，x & (~((1 << (n + 1)) - 1)）

有特殊意义的 & 位操作运算。第 260 题，第 201 题，第 318 题，第 371 题，第 397 题，第 461 题，第 693 题，

X & 1 == 1 判断是否是奇数(偶数)
X & = (X - 1) 将最低位(LSB)的 1 清零
X & -X 得到最低位(LSB)的 1
X & ~X = 0

1.2. tree ADT

1.2.1. binary tree

1.2.1.1. binary special tree

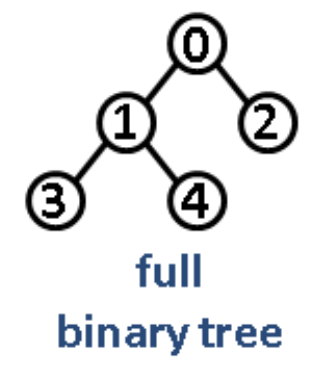
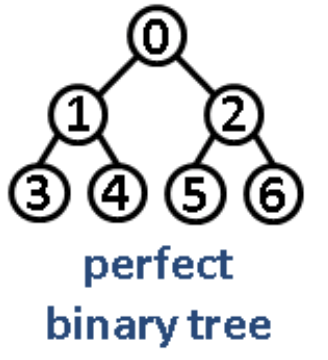
Intuition/Structure: Every node except the leaf nodes have two children.
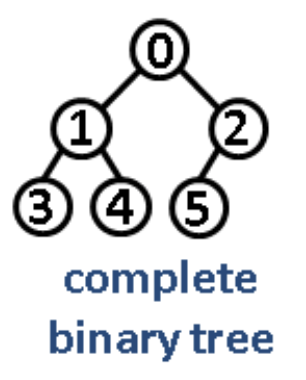
Intuition/Structure: Every level except the last level is completely filled and all the nodes are left justified.
Intuition/Structure: Every node except the leaf nodes have two children and every level (last level too) is completely filled.

1.2.1.1.1. segment tree

Usage : 线段树（segment tree），顾名思义，是用来存放给定区间（segment, or interval）内对应信息的一种数据结构。与树状数组（binary indexed tree）相似，线段树也用来处理数组相应的区间查询（range query）和元素更新（update）操作。

Difference with BIT: 与树状数组不同的是，ST也可以进行区间最大值，区间最小值（Range Minimum/Maximum Query problem）或s者区间异或值的查询。

Intuition/Structure:

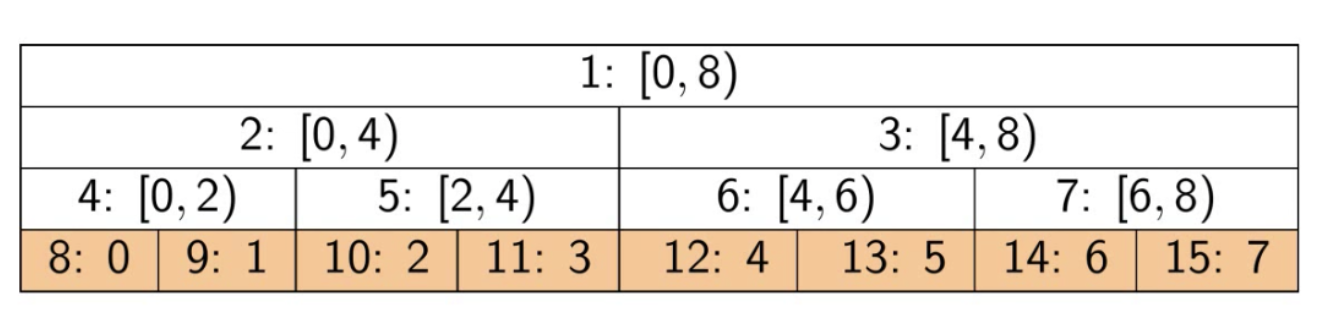
从数据结构的角度来说，线段树是用一个完全二叉树来存储对应于其每一个区间（segment）的数据。该二叉树的每一个结点中保存着相对应于这一个区间的信息。同时，线段树所使用的这个二叉树是用一个数组保存的，与堆（Heap）的实现方式相同。

e.g. 给定一个长度为N的数组arr，其所对应的线段树T各个结点的含义如下：

T的根结点代表整个数组所在的区间对应的信息，及arr[0:N)（不含N)所对应的信息。
T的每一个叶结点存储对应于输入数组的每一个单个元素构成的区间arr[i]所对应的信息，此处`0≤i。
T的每一个中间结点存储对应于输入数组某一区间arr[i:j]对应的信息，此处`0≤i。

以根结点为例，根结点代表arr[0:N]区间所对应的信息，接着根结点被分为两个子树，分别存储arr[0:(N-1)/2]及arr[(N-1)/2+1:N]两个子区间对应的信息。也就是说，对于每一个结点，其左右子结点分别存储母结点区间拆分为两半之后各自区间的信息。也就是说对于长度为N的输入数组，线段树的高度为logN。

segmentTree[1] = arr[0:8)
segmentTree[2] = arr[0:4)
segmentTree[3] = arr[4:8)
segmentTree[4] = arr[0:2)
segmentTree[5] = arr[2:4)
segmentTree[6] = arr[4:6)
segmentTree[7] = arr[6:8)
segmentTree[8] = arr[0]
segmentTree[9] = arr[1]
segmentTree[10] = arr[2]
segmentTree[11] = arr[3]
segmentTree[12] = arr[4]
segmentTree[13] = arr[5]
segmentTree[14] = arr[6]
segmentTree[15] = arr[7]

Note: actually we can make sure that the last layer is even. (total is odd, 1+2+4 is odd, last is even), 这个是可以证明的，也就是每两个最后节点上面都是和节点，证明的结果是需要2n-1个array来存放，这个逻辑是从”能放下“出发的，证明出来要用多少个来放。

Complexity:
- update:
  - $O(logn)$, 更新一个线段树的过程与上述构造线段树的过程相同。当输入数组中位于i位置的元素被更新时，我们只需从这一元素对应的叶子结点开始，沿二叉树的路径向上更新至更结点即可。显然，这一过程是一个O(logn)的操作。其算法如下。
    1
    2
    3
    4
    5
    6
    update(i, value):
    i = i + n
    segmentTree[i] = value
    while i > 1:
    i = i / 2
    segmentTree[i] = merge(segmentTree[2*i], segmentTree[2*i+1])
- query:
  - $O(logn)$, basically go through top to bottom.
- range_update & range_query
  - amotized $O(logn)$, I mean if lazy update is involved,
Advanced:
- discrete segment tree: you see the segment tree doesn't care what left right is ,so basically you can treat a range as a node if that range dot not split into small ranges.
- lazy update: actually range_update can be done without lazy update worst case $O(n)$ , but if overlapping update happens, lazy update can actually helps. Lazy can be done with set/ maxormin_set/ add/ sub/

1.2.1.2. binary search tree

1.2.1.2.1. vanila search tree

Operation:
- Insertion: 递归
- Deletion: 用左边最后一个/右边第一个换上来；或者用左边上来，然后递归删除左边。

1.2.1.2.2. red-black tree

Usage: for reducing height
Operation:
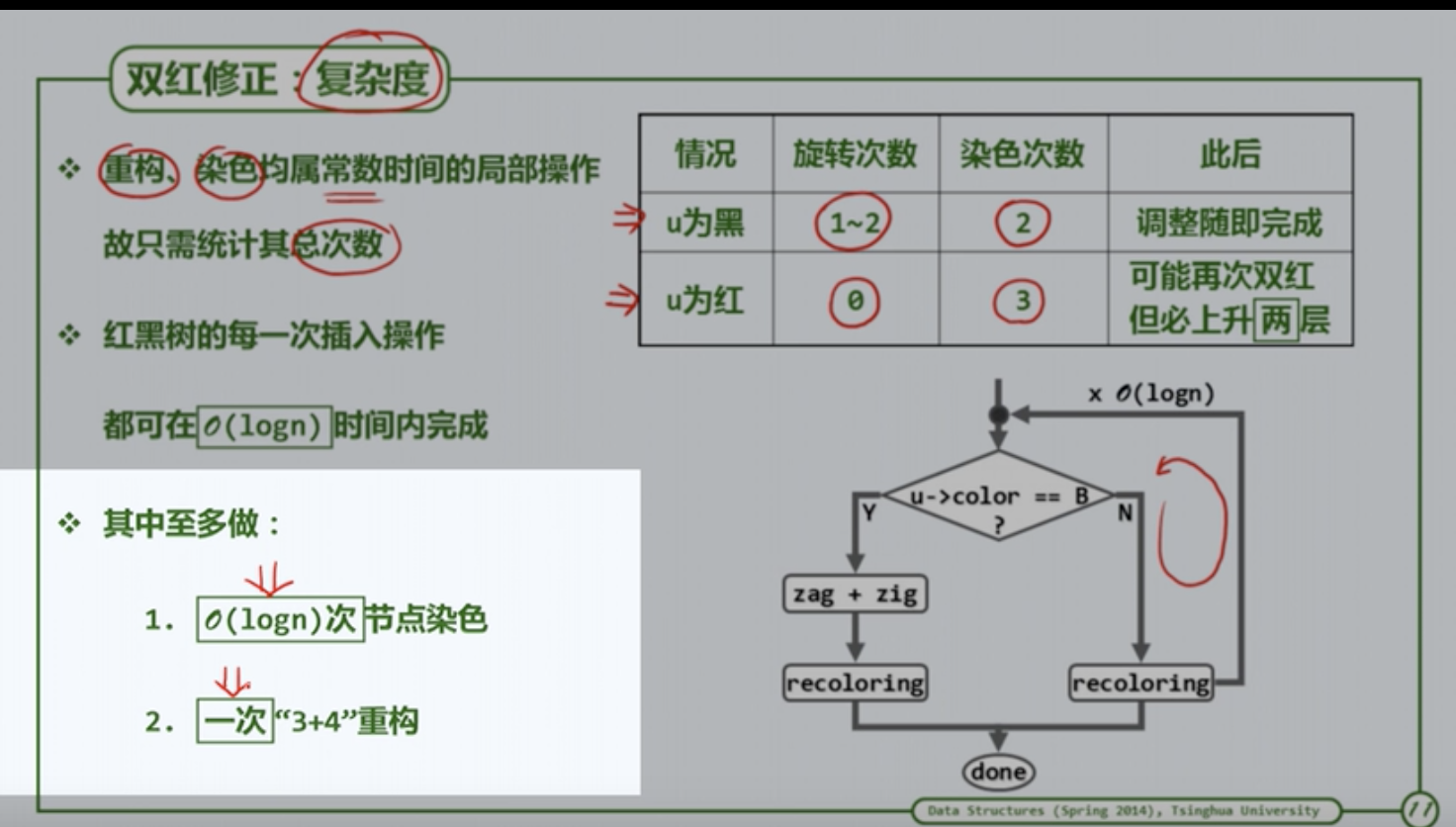
- insertion：插入一个红色节点然后改颜色。如果有双红冲突，就按照父母的兄弟节点是红还是黑判断。如果是红改色就可以->然后递归；如果是黑色就改色（叔父和祖父交换颜色）+然后祖父右旋然后做完了。最多logn染色+一次重构；如果是祖父，父，子不在同一边就先把父亲旋转调整到在同一边的情况。
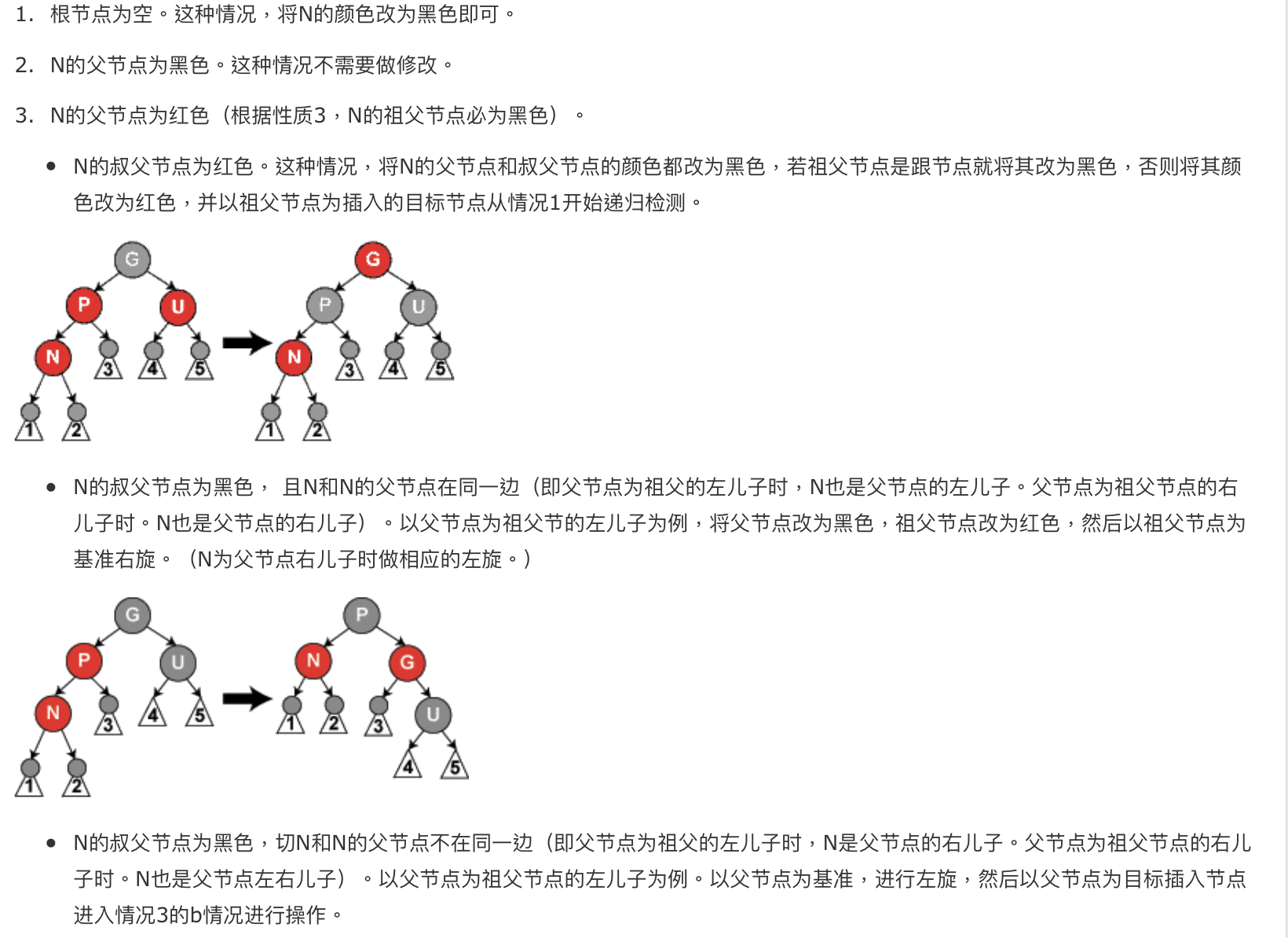
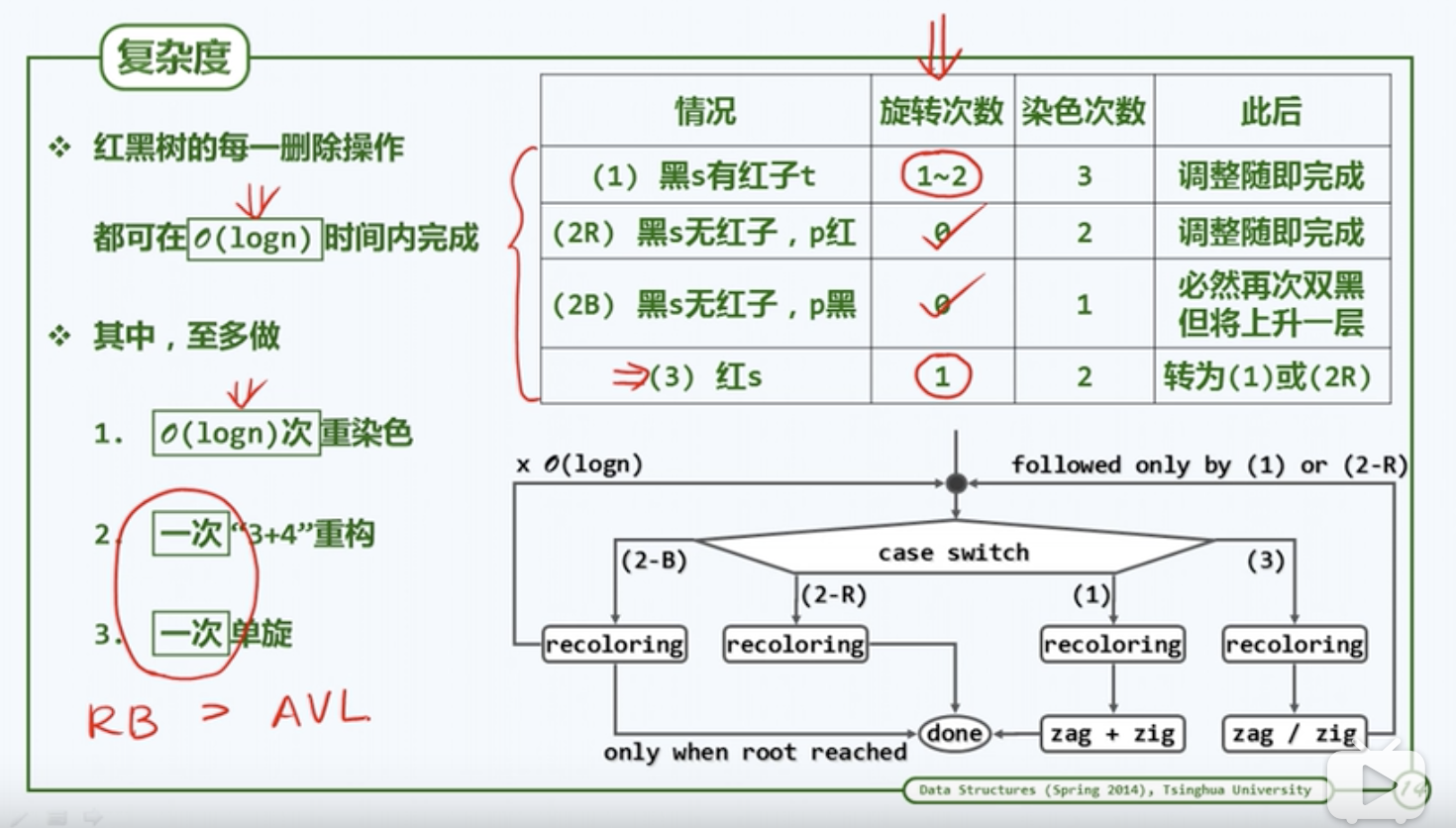
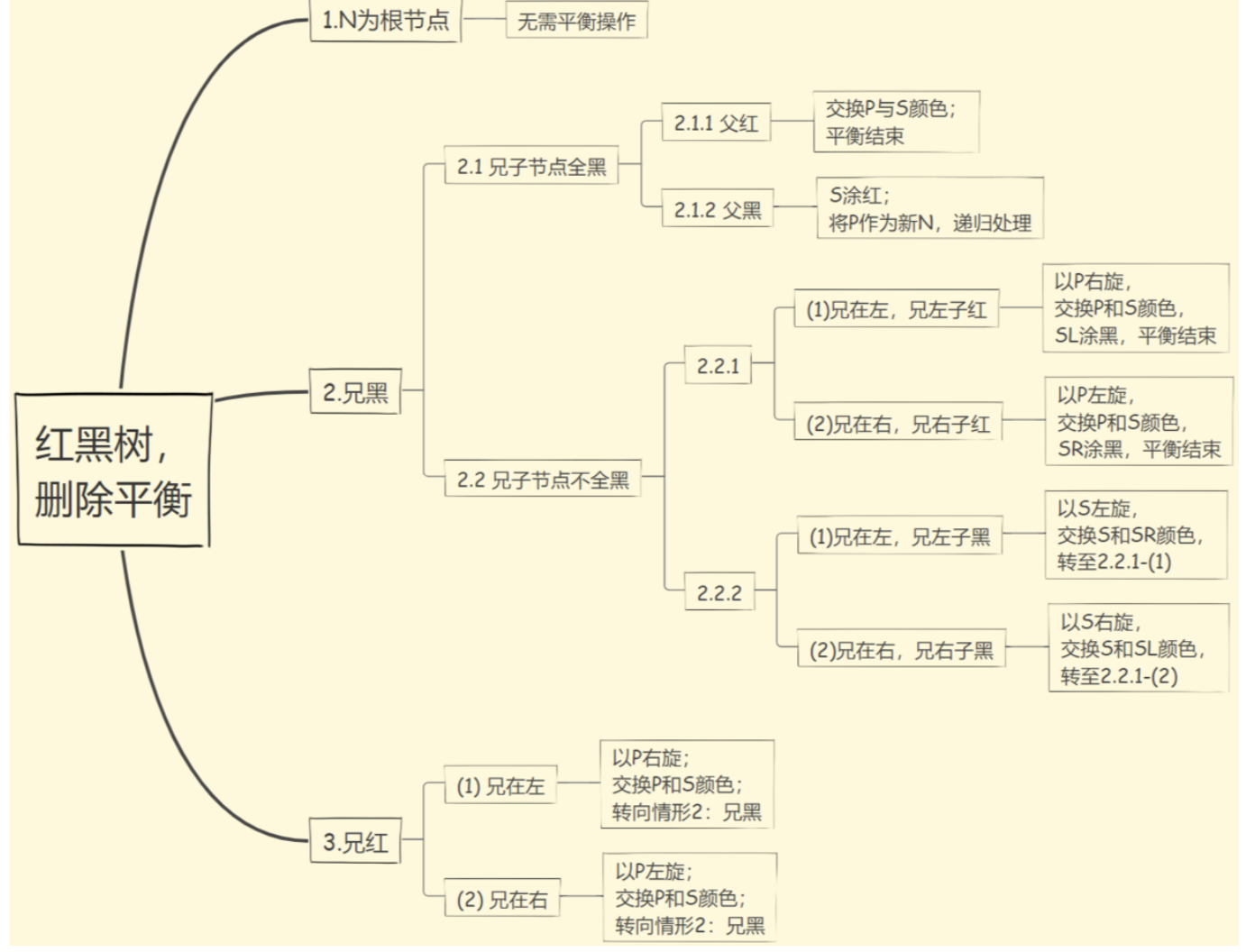
- Deletion ：从上往下删除。
  - 有两个子节点时候用后即节点代替。
  - 有一个子节点，就把子节点搞上来然后染色（此时红黑是不可能的）。
  - 无子节点，当是黑色时候需要平衡（最麻烦）
    - 兄红(3)->父亲必为黑所以父亲旋转下来然后交换SP颜色->转为兄黑情况->(1)/(2R)
    - 兄黑双黑子+p黑(2B)->S染红->子循环直到顶
    - 兄黑双黑子+p红(2R)->SP交换颜色->结束。
    - 兄黑有红子(1)->zig/zag+染色->结束。
  - 所以观察发现最多染logn次色，一次重构+一次单旋（先3后1)

1.2.1.2.3. avl tree

Usage: for reducing height, 左右高度差不大于1
Def: https://www.cnblogs.com/bigsai/p/11407395.html
Operation:
- insertion：先插再平衡，平衡就是ll,lr,rl,rr四个子树之间的比较，然后对应4个旋转名字都一样的，RL就是右子树LL，rootRR；LR就是左子树RR，rootLL。
- Deletion ：先删再平衡。

1.2.1.2.4. splay tree

Usage: for reducing height,A splay tree is a self-balancing binary search tree with the additional property that recently accessed elements are quick to access again.
Def:

https://www.cnblogs.com/csushl/p/10122047.html
Operation:
- insertion：先插再splay上去，splay的操作由ZIGZAG各一次，ZIG/ZAG连续两次，或者到跟节点就ZIG/ZAG一次。递归向上。
- Deletion：同理。

1.2.1.3. heap

1.2.1.3.1. skew heap

Usage: simpler leftiest heap
Def:same as leftiest heap except it swap children without testing.
Operation:
- insertion
- Deletion

1.2.1.3.2. leftiest heap

Usage:

前面说过，它能和好的解决"两个优先队列合并"的问题。实际上，左倾堆的合并操作的平摊时间复杂度为O(lg n)，而完全二叉堆为O(n)。合并就是左倾树的重点，插入和删除操作都是以合并操作为基础的。插入操作，可以看作两颗左倾树合并；删除操作(移除优先队列中队首元
Def:

https://www.cnblogs.com/skywang12345/p/3638327.html#a2
- Qua:
Operation:
- insertion：所有都是merge操作，root+左子树视为一片，一片一片切着来，谁小插入谁。然后从下到上交换左右。
- Deletion ：删了根然后合并。

1.2.1.3.3. bionomial queue

Usage:

左式堆将插入、合并和删除最小元的操作控制在O(logN)，尽管时间已经够少了，但二项队列进一步降低了这个时间。二项队列（binomial tree）以最坏时间O（logN）支持以上操作，并且插入操作平均花费常数时间。
Def:

https://blog.csdn.net/xitie8523/article/details/94467442
- Qua:

1.2.1.4. huffman tree

Usage: huffman code
Intuition:

1.2.1.5. binary index tree

Usage: BIT is used for efficient update & get_range_sum operations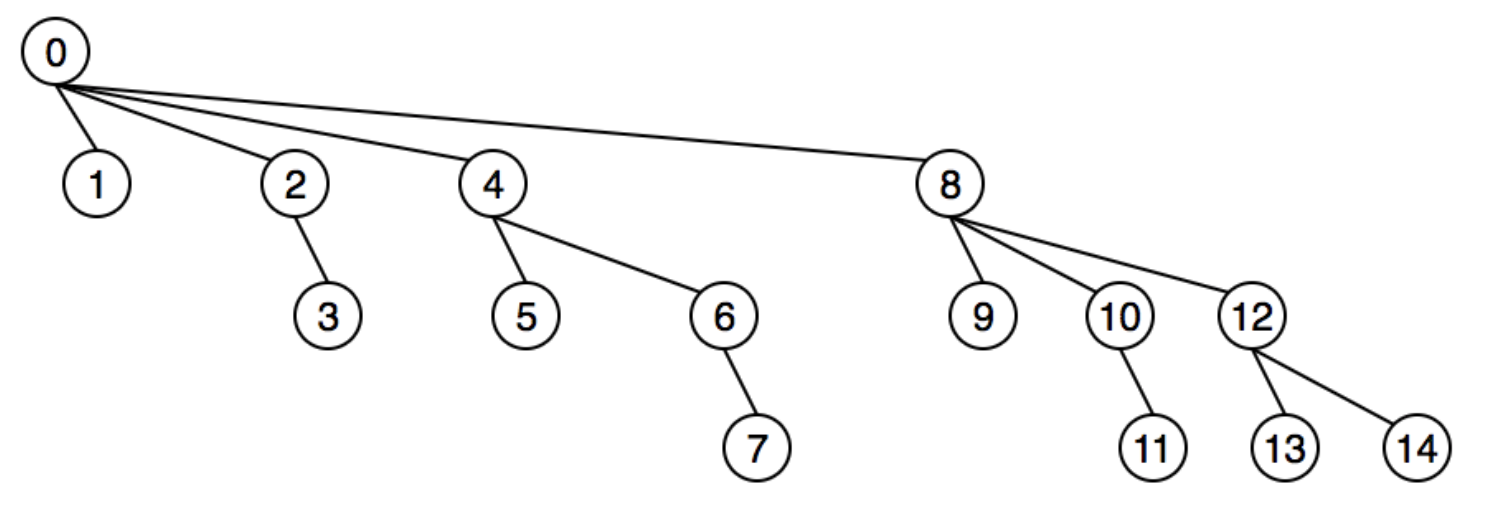
Intuition/Structure: cut range_sum into slices to reduce the time of updates

Note: so basically, the elements on $i_{th}$ layer, have i-1 ones in binary. And more importantly, have one more one after the last one of parent node (e.g. 8 is 10 00, 9 is 1001, 10 is 1010, 12 is 1100).So array[i] actually stores (eliminate last 1 of i) + 1 -> i(e.g. array[8]=[1,8]) So, the prefix sum is actually summing up all the ones => sum(13) = sum(1000)+ sum(0100)+sum(0010) +sum(0001). So the update becomes eliminating all ones.

Complexity:

build tree:
- $O(nlogn)$: inary Indexed Tree的建立非常简单。我们只需初始化一个全为0的数组，并对原数组中的每一个位置对应的数字调用一次update(i, delta)操作即可。
- $O(n)$: 此外，还存在一个O(n)时间简历Binary Indexed Tree的算法，其步骤如下(数组下标从0开始)：
  
  给定一个长度为n的输入数组list。初始化长度为n + 1的Binary Indexed Tree数组bit，并将list中的数字对应地放在bit[1]到bit[n]的各个位置。对于1到n的每一个i，进行如下操作：令j = i + (i & -i)，若j < n + 1，则bit[j] = bit[j] + bit[i]

get_range_sum:

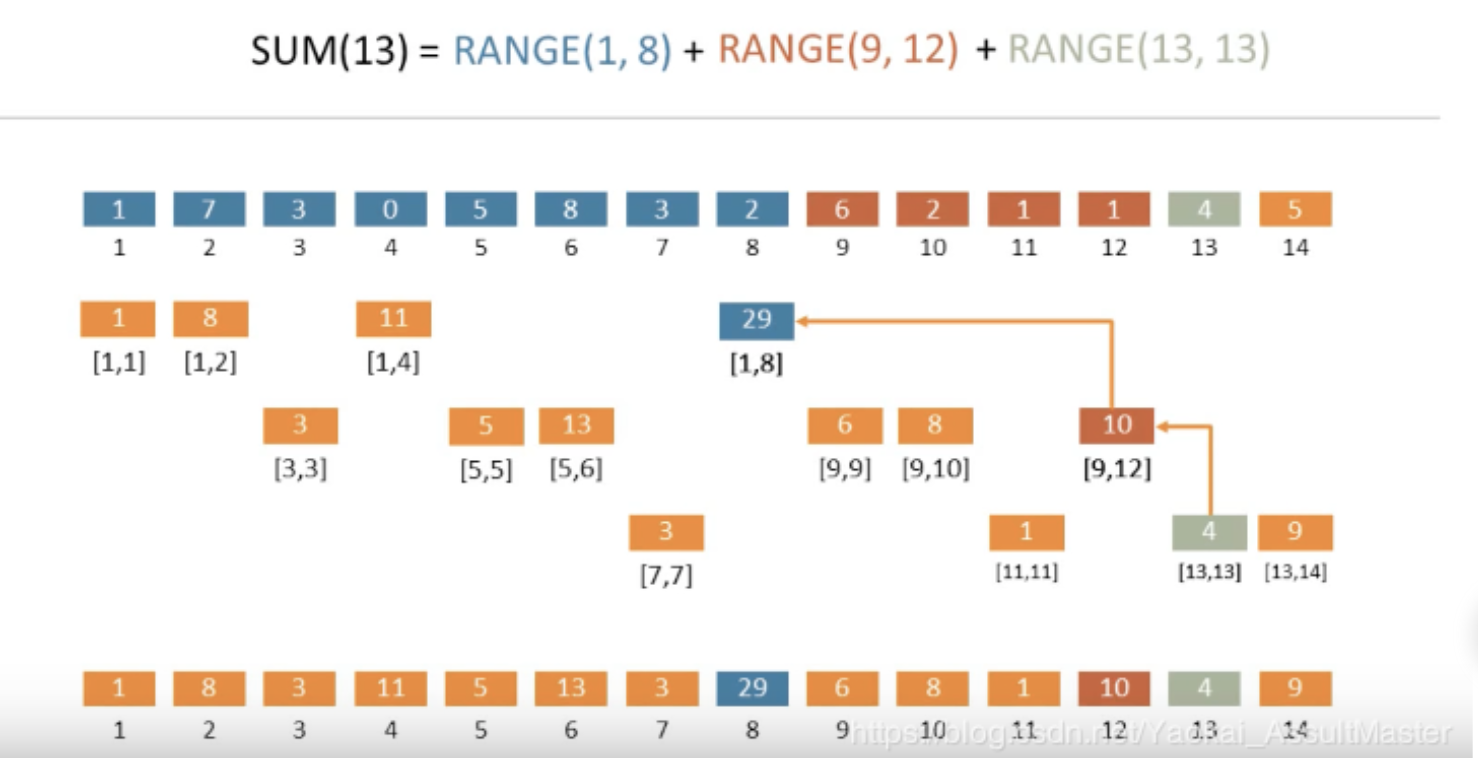
$O(logn)$: 可以发现，在这棵抽象的树种向上移动的过程其实就是不断将当前数字的最后一个1翻转为0的过程, from bottom to parent to root。基于这一事实，实现在Binary Indexed Tree中向上（在数组中向前）寻找母结点的代码就非常容易了。例如给定一个int x = 13，这个过程可以用如下运算实现：

prefixSum(13) = prefixSum(0b00001101)
  = BIT[13] + BIT[12] + BIT[8]
  = BIT[0b00001101] + BIT[0b00001100] + BIT[0b00001000]
x = 13 = 0b00001101
-x = -13 = 0b11110011
x & (-x) = 0b00000001
x - (x & (-x)) = 0b00001100

update:
- $O(logn)$: 从图中我们发现，从5开始，应当被更新的位置的坐标为原坐标加上原坐标二进制表示中最后一个1所代表的数字, 更新所有具有相同数量的1的比它大的节点以及一个一个去掉1的节点. 这一过程和上面求和的过程刚好相反。以int x = 5为例，我们可以用如下运算实现：
  1
  2
  3
  4
  x = 5 = 0b00000101
  -x = -5 = 0b11111011
  x & (-x) = 0b00000001
  x + (x & (-x)) = 0b00000110
  根据上面的分析，我们可以看出，对于长度为n的数组，单个update和prefixSum操作最多需要访问logn的元素，也就是说单个update和prefixSum操作的时间复杂度均为O(logn)。

1.2.2. general tree

1.2.2.1. B tree

Def:
- n-1个key，n个指针。
- 所有节点最少包含的指针为 (n)/2取上整，最多为n。
- 根节点最少两棵子树。
- i指针指向的孩子包含的所有key 大于等于key_i-1，小于key_i。
Operations: https://blog.csdn.net/xiaojin21cen/article/details/99830864
- Insertion: 不断插，插多了就中间分开然后中间提上去，如果中间提上去了还要分，就继续分。简而言之先insert，然后递归split。
- Deletion: 1）用二叉树删除同样的手法，递归到叶子结点。
  
  2）该结点key个数大于等于Math.ceil(m/2)-1，结束删除操作，否则执行第3步。
  
  3）如果兄弟结点key个数大于Math.ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束。
  
  否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。
  
  简而言之就是删到子节点，然后不断给该子节点借东西（要么是兄弟，只需一步；要么是父亲，借完了和兄弟合并然后递归到父亲）

1.2.2.2. B+tree

https://www.jianshu.com/p/71700a464e97

Usage: 高度很低，一般用于索引
Def:
- n-1个key，n个指针。
- 叶子最少包含的key为 n-1/2 取上整，最多为n-1。
- 非叶最少包含的key为 n/2 - 1，最多为n。
- 根节点最少包含的key为1.
- i指针指向的孩子包含的所有key 大于等于key_i-1，小于key_i。
- 每个key只是key，最终存在最后一层
Operations:
- insert: 插入到最后，然后依然是向上split。只不过最后叶子结点的split，中间节点保留在叶子，然后提上去一个key（B树是把中间节点提上去了），然后递归向上。
- delete: 同b树，(只不过借一个之后要修改父亲的索引，不会像父亲借东西而是直接和兄弟合并，合并后修改索引）然后递归向上也和b树有区别，b树的交换或者合并不会影响子节点，但是b+数在交换的时候也要看下面的节点）

1.2.2.3. Trie

Usage:
- for searching 1 string in a set of strings(when they have overlapping prefixes).
- for sorting in alphabetical order, very much like bucket sort.
- for we want to do the opposite to see if set[b,c,d,e] is in a, we just recursively search a.
Intuition/Structure: a mapping technique
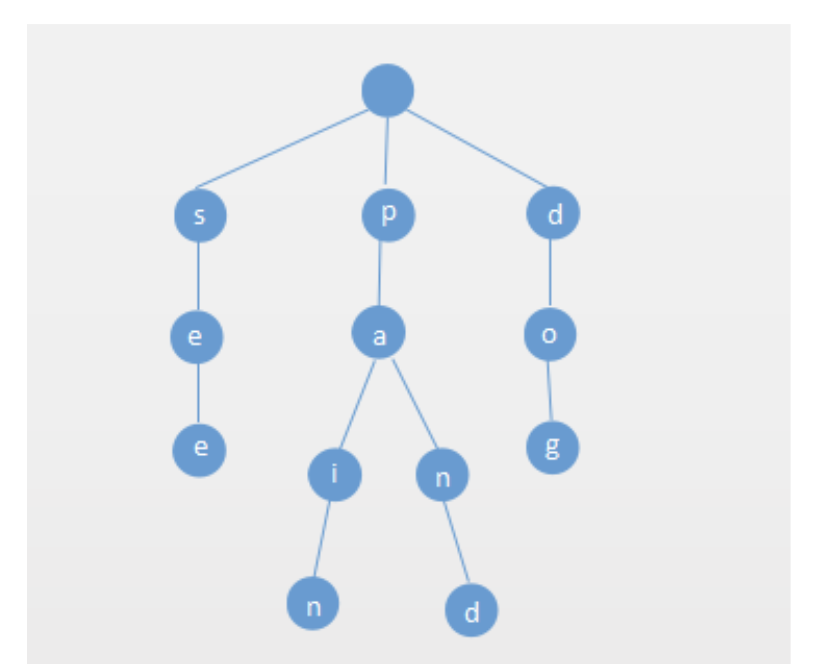
Complexity:
- search: $O(n)$ , actually it depends on the dataset, if no prefix is overlapped then it's $O(n)$, if all of them if overlapped, then it is $O(1)$

1.3. hashtable ADT

哈希表装填因子定义为：α= 填入表中的元素个数 / 哈希表的长度

因此，当Hash表中loadFactor==1时，Hash就需要进行rehash。rehash过程中，会模仿C++的vector扩容方式，Hash表中每次发现loadFactor ==1时，就开辟一个原来桶数组的两倍空间，称为新桶数组，然后把原来的桶数组中元素全部重新哈希到新的桶数组中。

1.3.1. hash function

1.3.1.1. 直接定址法

关键字的元素很少是连续的。用该方法产生的哈希表会造成空间大量的浪费，

1.3.1.2. 除留余数法

理论研究表明，除留余数法的模p取不大于表长且最接近表长m素数时效果最好，且p最好取1.1n～1.7n之间的一个素数（n为存在的数据元素个数）。例如：当n=7时，p最好取11、13等素数。又例图(5)：

1.3.1.3. 平方取中法

int Hash(int key){ //假设key是4位整数 key*=key； key/=100； //先求平方值，后去掉末尾的两位数 return key％1000； //取中间三位数作为散列地址返回 }

1.3.2. hash collapse

1.3.2.1. 开放定址

当一个关键字和另一个关键字发生冲突时，使用某种探测技术在Hash表中形成一个探测序列，然后沿着这个探测序列依次查找下去，当碰到一个空的单元时，则插入其中。基本公式为：hash(key) = （hash(key)+di）mod TableSize。其中di为增量序列，TableSize为表长。根据di的不同我们又可以分为线性探测，平方（二次）探测，双散列探测。 1）线性探测以增量序列 1，2，……，（TableSize -1）循环试探下一个存储地址，即di = i。如果table[index+di]为空则进行插入，反之试探下一个增量。但是线性探测也有弊端，就是会造成元素聚集现象，降低查找效率。具体例子如下图： 2）平方探测 4 以增量序列1，-1，4，-4…且q ≤ TableSize/2 循环试探下一个存储地址。

3）双散列探测 di 为i*h2(key)，h2(key)是另一个散列函数。探测序列成：h2(key)，2h2(key)，3h2(key)，……。对任意的key，h2(key) ≠ 0 ！探测序列还应该保证所有的散列存储单元都应该能够被探测到。选择以下形式有良好的效果： h2(key) = p - (key mod p) 其中：p < TableSize，p、TableSize都是素数。

删除不能直接删，否则会影响别人。

1.3.2.2. 链地址法

2. algorithms

Note: most of optimization problems of CS can be catagoried in combinatorial optimization, so here we consider only discrete math or CS problems. We use Def to denote the procedure of algorithm, Usage & Complexity are the same.

2.1. optimal search

Note:

### divide & concur

Usage: basically the base of all computer algorithms, to separate them to subproblems.
Def: divide & concur
- find subproblem
- improvise!
Complexity:
- guess & verify
- recursion tree: draw the tree and conpute all nodes(when the tree reaches O(1), if not guess )
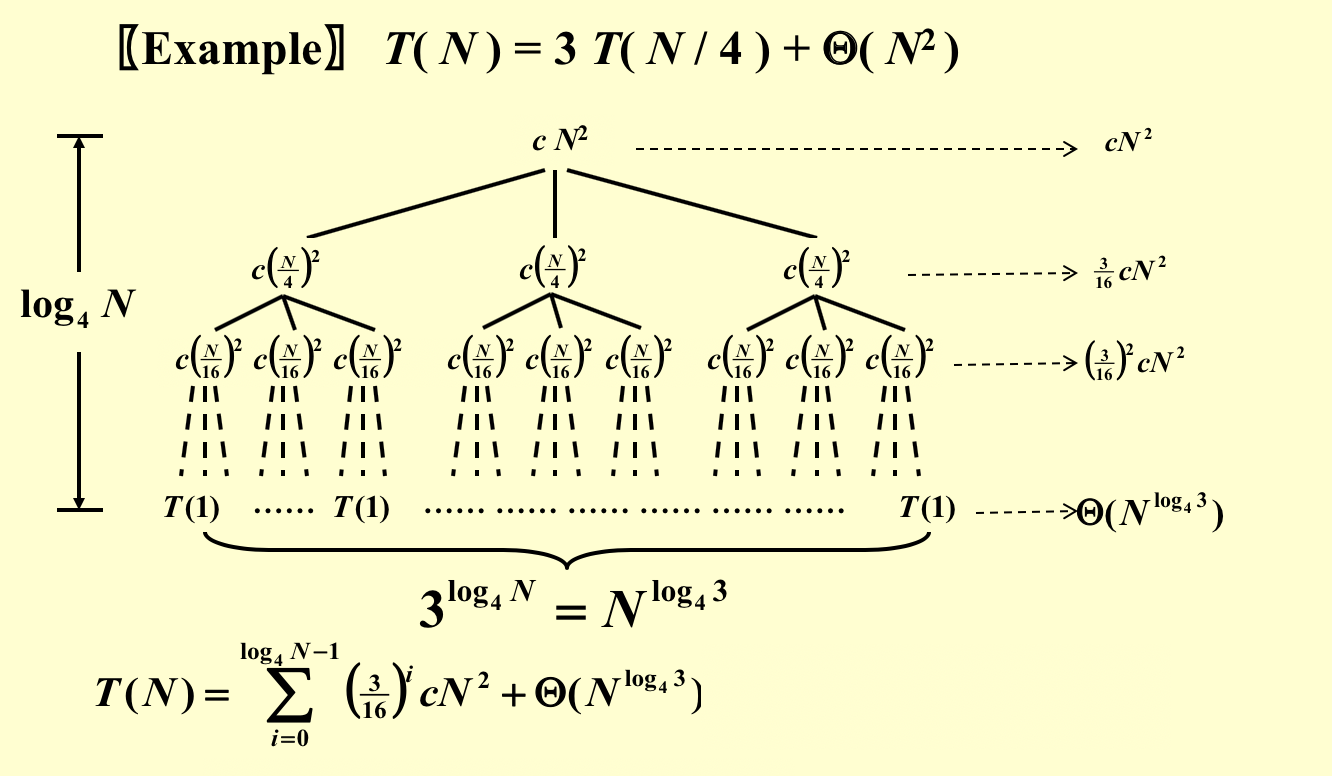
- master theory: 一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：
  
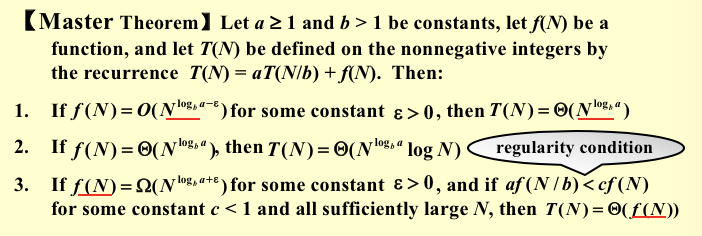
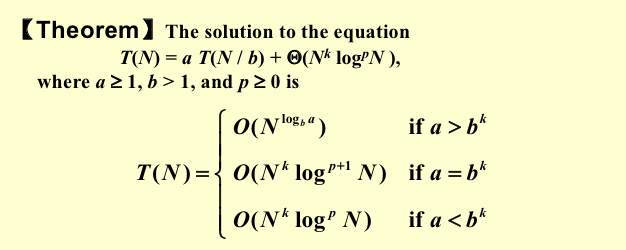  \[ T（n）= a T(n/b)+f(n) \\ \begin{equation} T(n)=\left\{ \begin{array}{**lr**} O(n ^{log_ba}) & \text{if f(n)<O(n^log(b,a))} \\ O(n ^{log _{b}a} log_bn) & \text{if f(n) =} \\ O(f(n)) & \text{if f(n) >} \end{array} \right. \end{equation} \]

2.1.1. depth first search

Usage: a way of searching subproblems
Def: depth first seach
- find subproblems
- set the meaning for the same level
- update next level status (how to search, or the propagation function)
  - independence: make sure no affecting over searches(to prevent duplicate you can [+] => do search => [-] or change the searching setting (with no refence) the common technique))
  - propagation: ...
- set iterative/ recursive
  - recursive => stop for{par_(lever+1)}
  - iterative(stack) array（necessary when special obervation simplifies problem)
- set terminal condition
- see if trimming or other advanced tricks can be used
Advanced: （简而言之从两方面优化：（1）第一尽量在保证正确性的情况下减少分支（相当于找最小数量的不相交的子集覆盖整个搜索区域，当然可以使用幂集但是就太慢了.）（2）如果减少分支还是会在不同分支有重复，使用DP。（3）如果是maxmin问题，分支可能会有上下界的剪枝。
- different-node optimization: if searching encounters exact same searching settings, memorize it, consider
  - is there possibility of encountering same searching settings on different levels?
  - is there any possibility that we cut those branches that doesn't affect optimal(usually on max/min problem). Use a global store => other branches affect trimming, usually when no duplicated path in all searching paths.examples: global visited[i][j] = 1: no duplicates
- same-node optimization: if we want to trim dfs, it's actually a step of narrowing down the domain => for a specific problem, we see what is the actual domain(the set contains the optimal): consider
  - is it full search(does it contain optimal?)
  - is there duplicates on the same level?(duplicate do not mean same problem, but it means unnecessary same outcome考虑是否重合可以从A分支是否包含B分支没有的内容或者相反来考虑 )) : e.g. sticker problem, going from the covering sequence is full and reduced duplicates, why? it is full since you can prove it by contrast, it is reduced because it cut off branches. Use parameter update => previous same branch affect trimming. examples: &grid[i][j] = 1
- other specific problem requests optimization:
  - if we want to return when we find a solution but not all solutions, we can terminate internally(by the next line after subproblem) or externally(by the entrance of subproblem).
  - if we want greedy in some circumstances(trim), then we have to return more than usual=>return the status of result to trigger trimming.
  - if sometime starting nodes are too many, try to search from end to start.(e.g. 417. Pacific Atlantic Water Flow)

2.1.1.1. tail recursive

Def: tail recursive

顾名思义，尾递归就是从最后开始计算, 每递归一次就算出相应的结果, 也就是说, 函数调用出现在调用者函数的尾部, 因为是尾部, 所以根本没有必要去保存任何局部变量. 直接让被调用的函数返回时越过调用者, 返回到调用者的调用者去。尾递归就是把当前的运算结果（或路径）放在参数里传给下层函数，深层函数所面对的不是越来越简单的问题，而是越来越复杂的问题，因为参数里带有前面若干步的运算路径。

Note: 尾递归是极其重要的，不用尾递归，函数的堆栈耗用难以估量，需要保存很多中间函数的堆栈。比如f(n, sum) = f(n-1) + value(n) + sum; 会保存n个函数调用堆栈，而使用尾递归f(n, sum) = f(n-1, sum+value(n)); 这样则只保留后一个函数堆栈即可，之前的可优化删去。

Example:
1
2
3
4
5
6
7
8
9
10

int FibonacciTailRecursive(int n,int ret1,int ret2)

{

if(n==0) return ret1;

return FibonacciTailRecursive(n-1,ret2,ret1+ret2);

}

2.1.2. breadth first search

Usage: have to satisfy all otherwise we could use (DFS + meme + trim>shortest)
- when asked to find shortest and depth_tree > shortest
- when the same level information can help us with trimming.
Def: bfs
- find subproblem
- set the meaning for the same level,
  - set update status for next level (how to search, or the propagation function)
  - make sure not affecting other searches
- set iteration/ recursive (prefer recursive) =>
  - iterative: stop for{same level} onlyone(lever+1)
  - recursive: while(stop) { for{same level} update} (actually no need to recur)
- set terminal return or continue;
- see if advanced technique can be used
Advanced:
- dp: avoid necessary branches
- trimming: return before iteration;

2.1.3. dynamic programming

Usage: useful when you can separate subproblems
Def: dynamic programming
- find overlapped subproblem
  - basically, you can put the ans on index/value. (e.g. problem 871, putting ans which is the number of stations on value would be like dp[i] is the smallest number of stations from i to end, putting ans on index would be like i is the stations taken and dp[i] would be the max distance traveled.) to make it more accurate, we want to separate the problem by stations which is a natural thought, so DP[i] is a must-do. then we have the distance and number of stations taken which is information we can't throw away, solution 1: dp[i][distance] = {number}, solution 2: dp[i] = {number & distances}, solution 3: dp[i][number]={distances}, apparently, solution3 is the easiest way since i and number are all integers.
  - advanced technique i: if putting parameter on index is too costy, you can put it on value (e.g. 871, distance of travelling is an important parameter and if you put it on index it is too costy, so we choose the alternative, putting it on value.)
  - advanced technique: if 2 subproblems can combine to 1, better do it; you can see here we use self.rob(root) = [a, b] to combine them.
    1
    2
    max(self.rob(root.left, 0) + self.rob(root.right, 0),
    self.rob(root.left, 1) + self.rob(root.right, 1) + root.val);
- set a propagation equation
  - independence: have to make sure all subproblems are independent
  - how to find equation: find problem features: for a special problem like 664 painter, we start by realizing that first element will always be printed once, which leads to a natural thought, how long will that print end, which leads to a intuitive equation.
  - advanced: trimming: consider carefully which element is used, so like if max(dp[...]) is used, consider putting max in a single dp[i] so you can cut branches.
- set recursive or iteration
  - iteration: find update sequence
    - output true/false
    - equation is easy (subproblem are easy to find, e.g. in a top-down manner ) || update sequence is easy to find( since this is what we want if we want bottom-up)
  - recursive: DFS related
    - output not int/bool (in this case will have to use a map)
    - propagation is hard (subproblem not easy to find, e.g. in a top-down manner)
- set init values and margin conditions.
Advanced:
- time (bu vs td, time complexity = relationships * c.(why? because in bu all relationships are used to calculate every elements, in td every elements is used once(prove by contradiction, if twice then you are not saved)). Then, in bu c = operations, in td c = call&return, so bu is more preferable! )
- finding pivot indexes is more preferable using bottom-up implementation!

2.1.4. binary search

Usage: useful when you can relate a problem to a monotone array.
Def: binary search
- find subproblem(split in 2 subproblems)
- set find a monotone array and ditch one of of problems (unique propagation equation), so monotone array is useful so we can easily trim one of the branches!
- set recursive or iterative (perfer iterative since it make things easier)
- set the margin conditions
  - l<r, l+r/2, if(array==1) r = mid, l = mid + 1, when array is 0000011111 and we want the first 1.
- l<r, ceil(l+r/2.0), l = mid, if(array!=1) r = mid - 1; when array is 000001111 and we want the last 0, the point is to make sure [l, r] always have the thing you want.

2.1.5. greedy search

Usage: only special problems can use this. one way of trimming all other branches except for the greedy optimal one/ or a way of searching directly to the results instead of following a path of searching/ or directly solving subproblems
Def: greedy search
- (think of greedy when searching is too large)
- find the smallest problem and prove greedy optimality
- prove that from smallest to i+1 using greedy(like a easy dp equation) is optimal (compare to not smallest to i+1)
Note: the hardest part is always proving optimality.

2.1.6. branch & brand

2.1.7. random search

2.1.7.1. local search

Usage:
Def: local & search

####simulated annealing search

Usage:
Def:

2.1.7.2. metropolis search

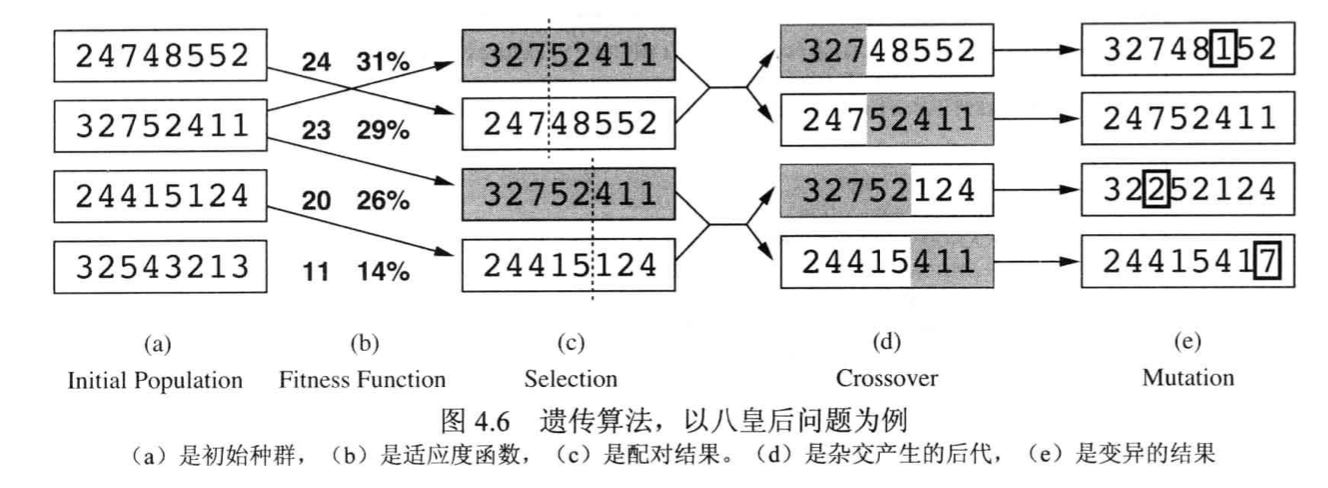
2.1.7.3. genetic search

Def:
- Note: procedure

2.1.7.4. randomize search

Usage:

2.1.7.5. greedy search

Usage: greedy here is to minimize complexity. It could be seen as some degree of randomization.
Note: greedy search here need not to be optimal

2.1.8. heuristic search

Usage: the whole idea of heuristic is to use information we have to build a f(n) and choose the min f(n) node

2.1.8.1. greedy best first search

Def: f(n) = h(n) (design h(n))

2.1.8.2. A*

Def: f(n) = g(n) + h(n) (design g(n) & h(n))
- Theorem: to ensure optimality
  1. constrait on h(n)

2.2. adversarial search

Def: search tree

2.2.1. max min search

Def: minmax(s) = when it is max node, action is to reach max in next level.
Def: min max algorithm
- Note: it has to do a complete dfs first. It is basically a double DP problem, max-dp depends on min, min-dp depends on max.

2.2.2. $\alpha \& \beta$ trim

Def: 基本思想：每个MAX结点设置一个目前已知下界alpha，每个MIN节点设置一个目前已知上界beta。alpha，beta会向下传递，同时也会在向上时候更新。当一个max节点alpha大于等于beta时，就意味着对于其父节点来说，此max已经废了，所以剪掉剩下的枝。注意到alpha还是beta只针对当前层，与前面的层无关，也就是说剪枝也只是剪一层。
- Note:
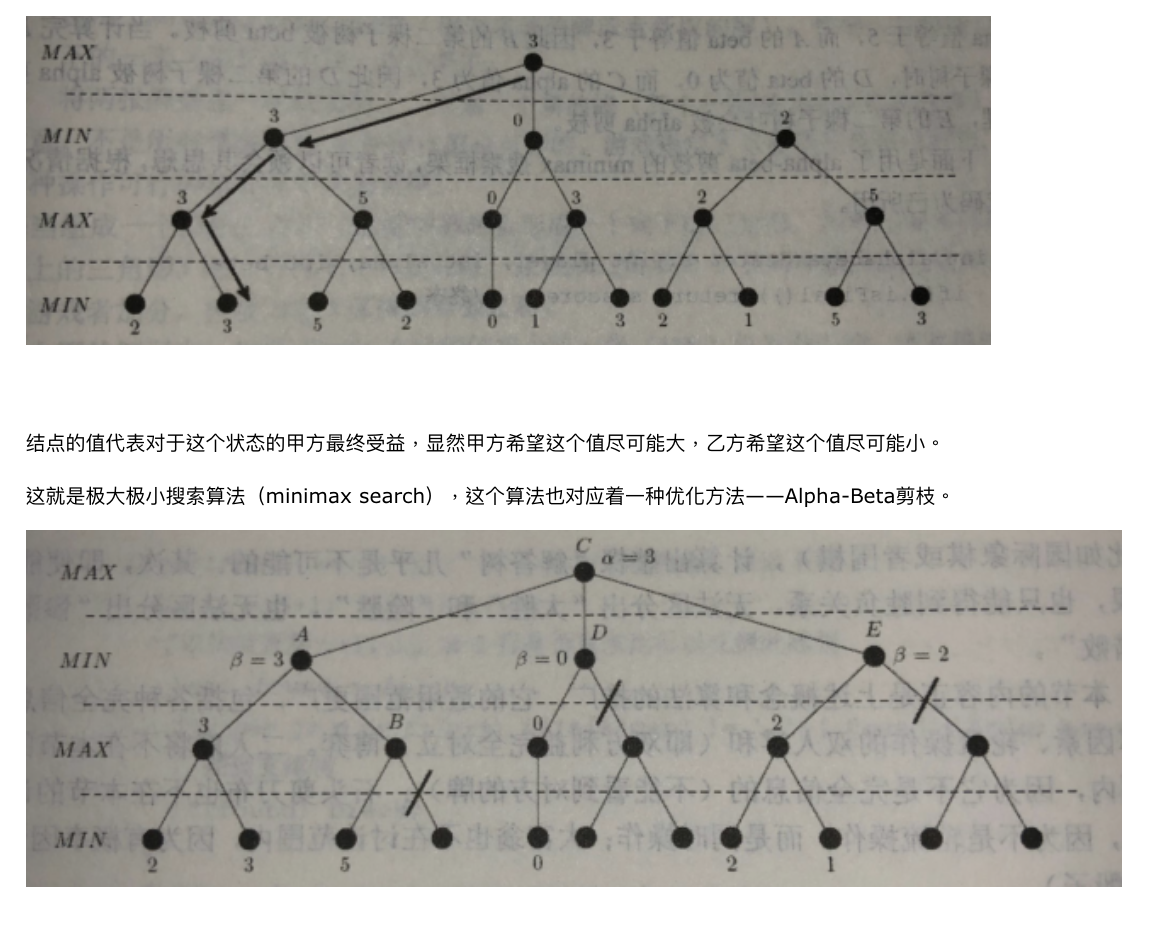
- Qua: 需要注意的是，剪枝的效果与树节点的访问顺序有关。

2.2.3. Monte Carlo search

Usage：instead of expanding the tree completely, we can choose a node by simulating.

https://blog.csdn.net/qq_16137569/article/details/83543641

2.3. sort

2.3.1. insertion sort （从左边开始固定）

Def: algorithm
1. Iterate over all elements
2. 把该element从后往前遍历之前放入被排序好的。
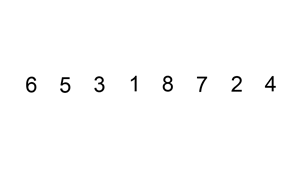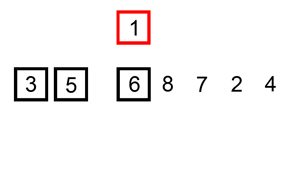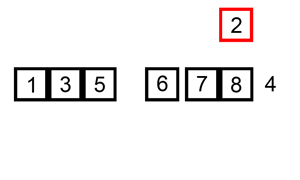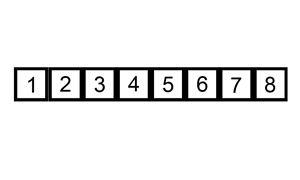
Insertion Sort
- Note: Very inefficient for large datasets
- Note: Better than selection sort and bubble sort for small data sets,

2.3.2. bubble sort （从右边开始固定）

Def: algorithm
1. Iterate over all elements
2. For each element:
Swap with next element if out of order
1. Repeat until no swaps needed
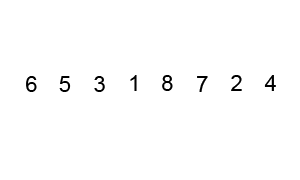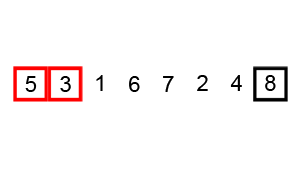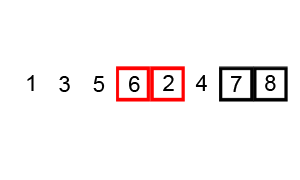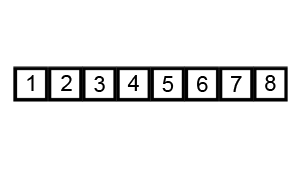
Bubble Sort
- Note: Much worse than even insertion sort, Very inefficient for large datasets
- Note: Easy to detect if list is sorted,

2.3.3. selection sort （从左边开始固定）

Def: algorithm
1. Iterate over all elements
2. For each element:
If smallest element of unsorted sublist, swap with left-most unsorted element

Selection Sort
- Note: Very inefficient for large datasets
- Note: Low memory usage for small datasets

2.3.4. merge sort

Def: algorithm
1. Divide list into smallest unit (1 element)
2. Compare each element with the adjacent list
3. Merge the two adjacent lists
- Note:
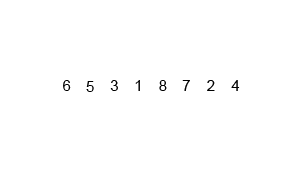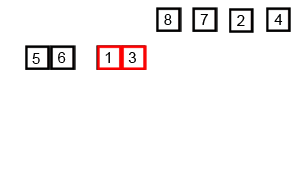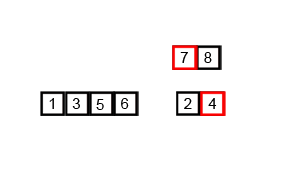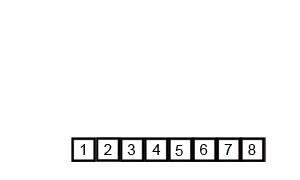
Merge Sort 2
- Note: Slightly worse than Quicksort in some instances, Still requires O(n) extra space
- Note: Nearly always O(nlog(n)), Can be parallelized, Better space complexity than standard Quicksort, High efficiency on large datasets
Complexity :
- O(n logn):T(n) = 2T(n/2) + n
- n + 2 * n/2 + 4 * n/4 + n * 1

### quick sort

Def: algorithm
1. Choose a pivot from the array
2. Partition: Reorder the array by swapping so that all elements with values less than the pivot come before the pivot, and all values greater than the pivot come after. (fixing the last element)
3. Recursively apply the above steps to the sub-arrays
- Note: partition
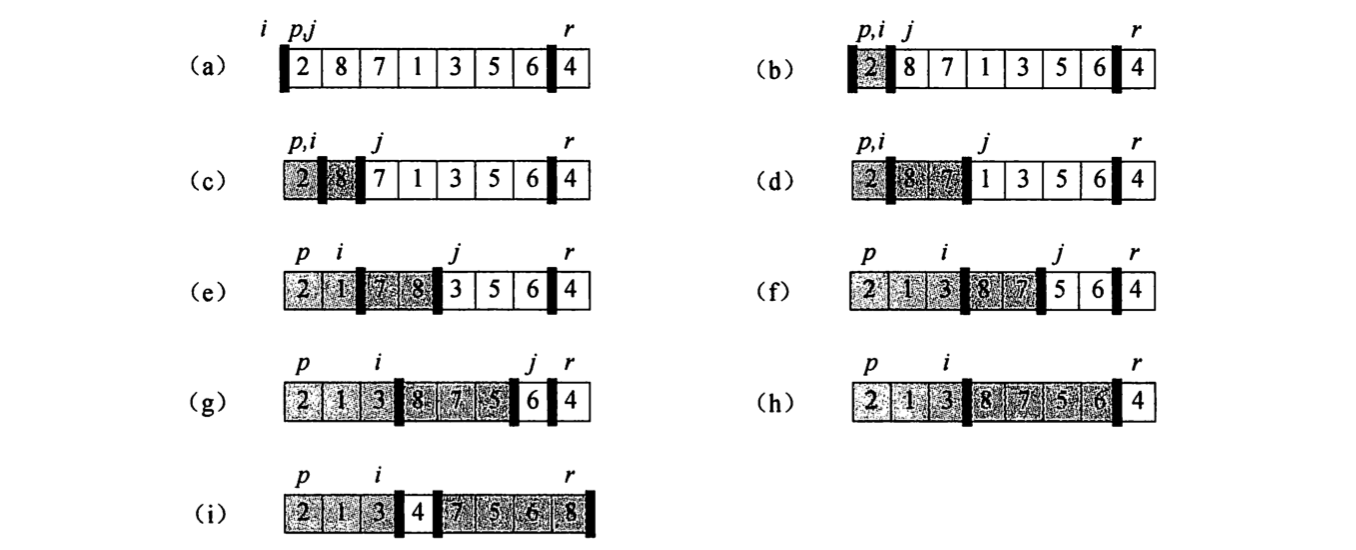
- Note:
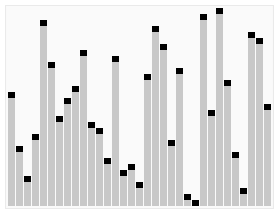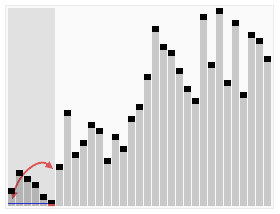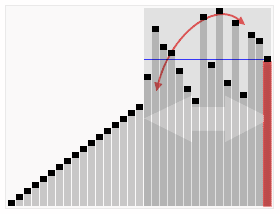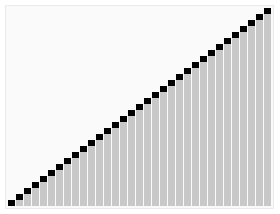
Quicksort
- Note: Not stable (could swap equal elements), Worst case is worse than Merge Sort;
- Note: Can be modified to use O(log(n)) space, Can be parallelized, Very quick and efficient with large datasets
Complexity:
- worst case: $O(n^2)$
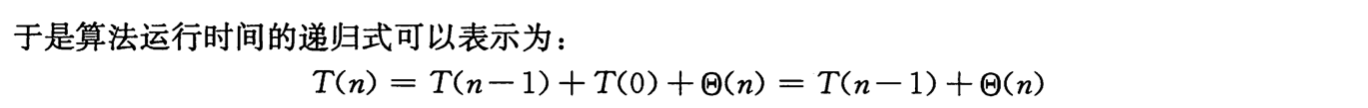
- best case: $O(n logn)$
- expected case: $O(n logn)$
  
  通过
  
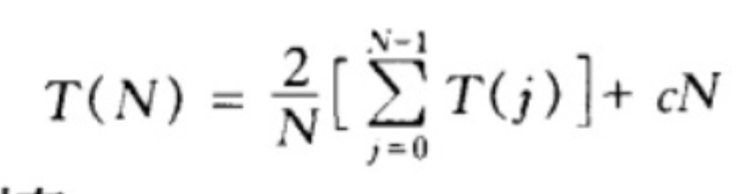
  找相邻递推关系：乘N，相邻两项相减
  
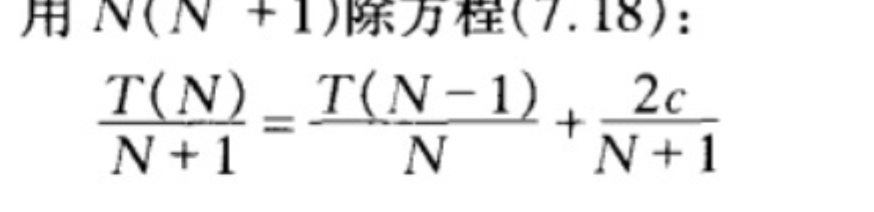
  使用递推关系：叠缩
  
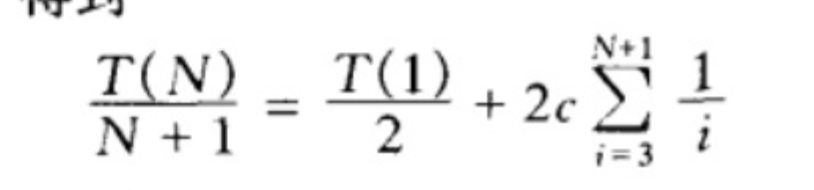
  右边是已知的logn，最后是欧拉常数

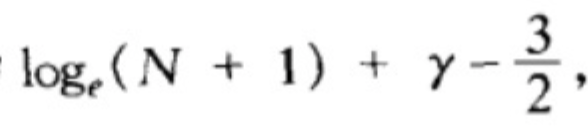
Alternative: random version
- q

2.3.5. heap sort

Def: algorithm -

2.3.6. count sort

Def: algorithm
1. count all elements
2. put them in correct order
- Note:
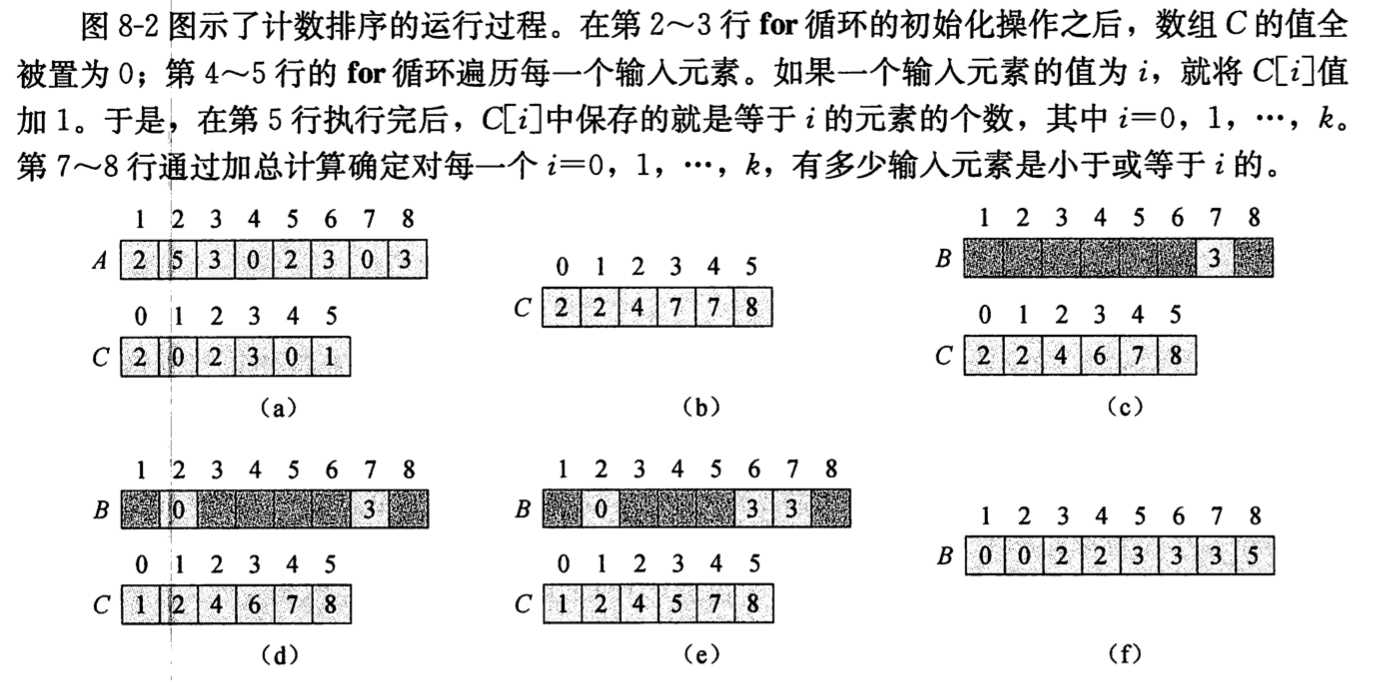
Complexity:
Qua: stable

2.3.7. bucket sort (improved count sort)

Def:
1. put elements in the right bucket
2. sort each bucket
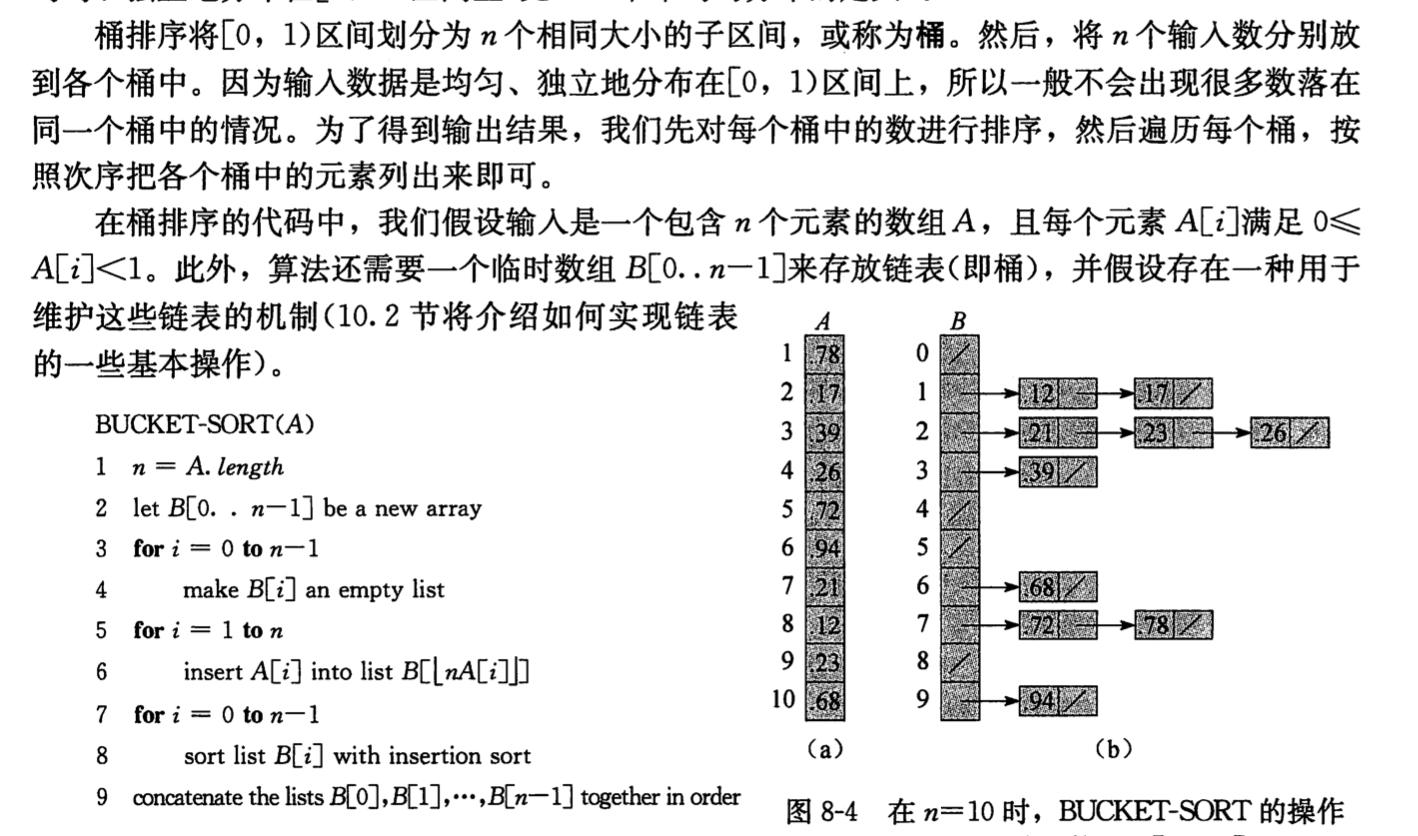
Note: count sort = bucket sort with infinite buckets, insertion sort = bucket sort with 1 bucket.

2.3.8. radix sort

Def:

stable sort on each radix
Complexity:

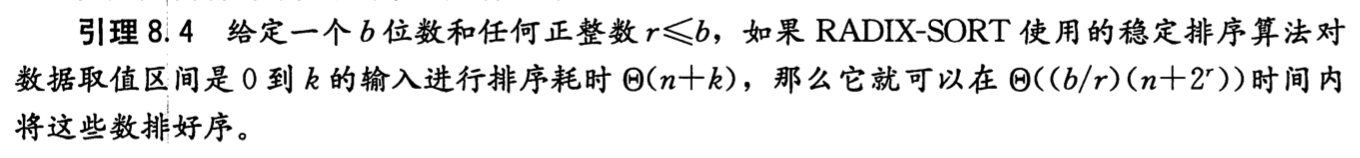
2.4. graph

2.4.1. topological sorting

Usage: topo sort can be used to do longest path
Note: any nodes on one layer are larger than connected last layer.
Def: bfs with degree

2.4.2. union find

Usage:
- used to find if 2 elements are in the same category
- used to find how many connect component/ circles are there
- efficient when overlapping(changing many times for a single node)
Def:
- find the nodes
- find the node union conditions (could use trick here to shorten n comparisons to constant m ).
Complexity:

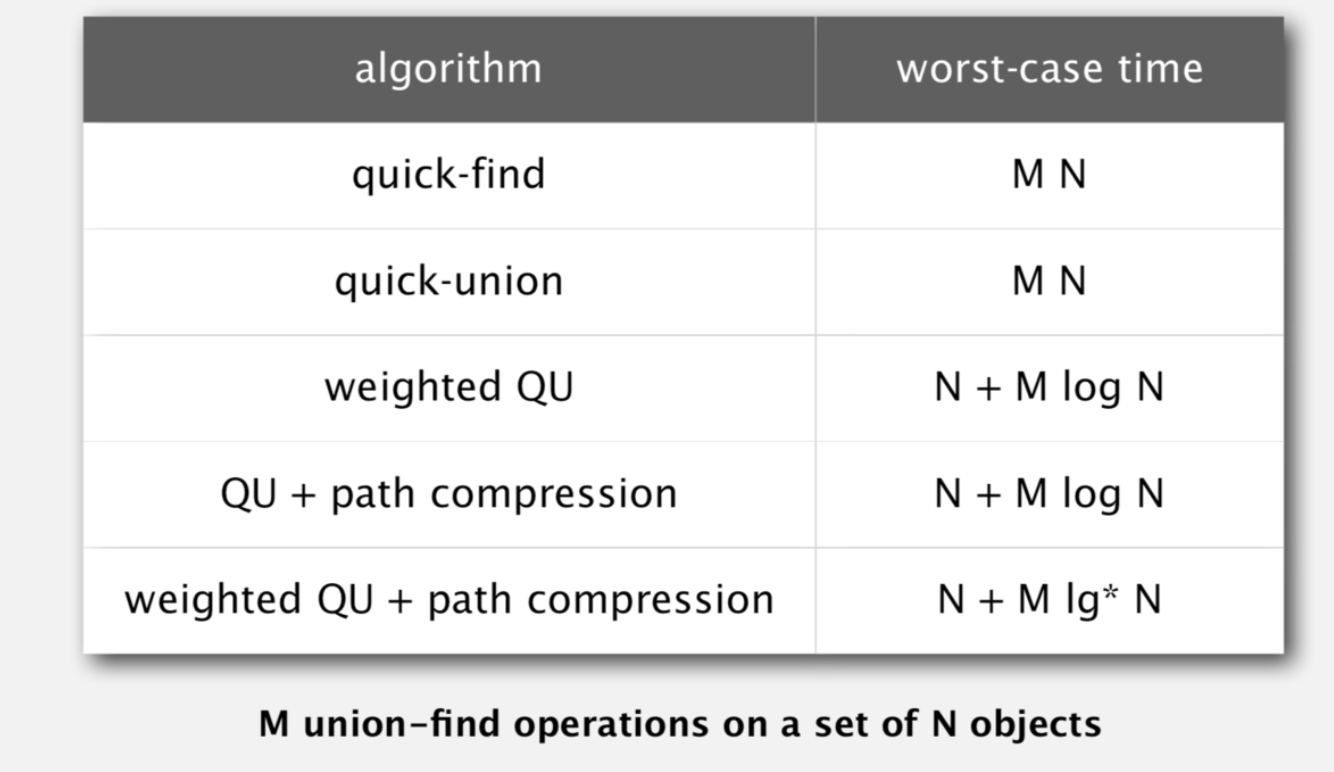
2.5. string

2.5.1. rolling-hash

Usage: hash a string => determine if string a == string b in O(1)
Def:

https://zhuanlan.zhihu.com/p/67368838
Complexity: $O(n) $ preparation & $O(1)$ calling

2.5.2. largest suffix

Usage; finding largest suffix
Def:

2.6. stats

2.6.1. moore-voting

Usage: for finding mode
Def: 摩尔投票法基于这样一个事实，当一个数的重复次数>=数组长度的一半，每次将两个不相同的数删除，最终剩下的就是要找的数。 [candidate, count] =(at ith time) [candidate, the count candidate in [0:i] - other different], and when count < 0 => we set candidate = num[i].
- Proof: ez proof, when count>=0, it is always guaranteed, when count<0, then elements before i is ruled out from the candidates, so we choose a new one.

2.6.2. Random Generator

Usage: use RandM to generate RandN
Def: use randM + (randM()-1)*M (here has to M) to generate randM^2, and use while(res>N) {res = randM^2} to generate randN.
- Proof: p(randM + (randM()-1)M = k) = p(k/M = g, k%M = q) = 1/M 1/M (key point here is to make k%M correct, (randM-1)*Q has to be modM=0, so we choose Q = M (or kM).

2.6.3. Fisher–Yates shuffle

Usage: to shuffle an array randomly
Def:
Complexity : O(n) / space O(1)

2.6.4. Reservoir Sampling

Usage: randomly choose a element without knowing all N.
Def: 我们可以：定义取出的行号为choice，第一次直接以第一行作为取出行 choice ，而后第二次以二分之一概率决定是否用第二行替换 choice ，第三次以三分之一的概率决定是否以第三行替换 choice ……，以此类推。由上面的分析我们可以得出结论，在取第n个数据的时候，我们生成一个0到1的随机数p，如果p小于1/n，保留第n个数。大于1/n，继续保留前面的数。直到数据流结束，返回此数，算法结束。
Complexity : O(n) / space O(0)

2.6.5. random number

Usage: how to get random number
Def: random number
- Qua:

2.6.5.1. add mod

Def :
- Qua: cons

2.6.5.2. linear mod

Def:
- Qua: cons
- Qua: cons
Def: primitive root
- Theorem:

2.6.5.3. non-linear mod

Def :
Def:

2.6.5.4. multi-step non-linear mod

Def:

2.6.5.5. Mersenne Twister

Def: init
- Note:
Def:
- Note :
Def:
- Note:

2.6.5.6. high dimension

Def :

2.7. other

3. Leetcode

Note: here are the notes of leetcode problems, I think the way of analyzing a problem is to follow 2 steps:
- ways of solving: 1) searching? 2) greedy? 3) math proved?
- ways of implementing: various data structures

3.1. int

3.1.1. no.7 iterate & reverse int

careful:
- remember the INT_MAX & INT_MIN, and that INT_MAX + 1 = INT_MIN
- and that any int will trancate to [INT_MIN, INT_MAX] if overflow.
- that string numbers n are bad for comparation.

3.1.2. no.9 iterate & reverse int 2

key:
- observation: some can compare when all is flipped over.
careful:
- remember it is difficult to yield the first character of a int,

3.1.3. no.13 iterate & assign

key:
- observation: examine the problem carefully

3.2. string

3.2.1. no.28 iterate

key:
- observation: can use substr
  1
  haystack.substr(i,len);

3.2.2. no.859 iterate & swap

key:
- observation: consider all circumtances

3.3. vector

3.3.1. no.26 iterate & erase/assign

careful:
- vector after erase, iterator position change!!!, so reassgnment is neccesary(all iterators need to be reassigned), so erase is not preferable during iteration!.
- try to use move & assign tech instead of erase.
  1
  2
  a = gg.erase(a);
  b = a;

3.3.2. no.665 iterate & change value (math problem)

key:
- observation:
  1. 注意这个算法只是（只改变一次的最优策略）这种情况，并非改变（改变最少次数）的全局最优。所以是局部最优解，但是考虑到只改变一次这种情况，就是i j出问题，那么解决i, j 必然要1次的变动。如果能用一次解决，所以改变i或者j其中一个一定能解决这个问题。所以考虑改变i和j能解决问题的区别，在默认改变一次能解决所有问题的假设下，只有一种情况改变j才能解决：就是以下情况。所以才这么做。
  2. 以上解释太蠢了，我们直接把所有四种情况能用一次改变解决的画出来即可，然后设计一个算法解决它，如果这个算法能解决，那么必然符合情况，不能解决就不符合。
  3. that for every xi > xj (i < j), either i or j have to be changed, and of course we want i to change since i decrease can at most amend (n-i) relationships, and j increase may at most amend j relationships. since we go from i=0 to n-1, the left side of i we assume is already fixed. the only condition we prefer j over i is that j can change both i-k, i-m. so we push j into a set to prevent that from happening.

3.3.3. 57. Insert Interval

key

observation:

class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
        int s = -1, e = -1, sz = intervals.size();
        if(!sz || newInterval[1]<intervals[0][0]){
            intervals.insert(intervals.begin(), newInterval);
            return intervals;
        }
        if(newInterval[0]>intervals.back()[1]){
            intervals.insert(intervals.end(), newInterval);
            return intervals;
        }
        for(int i=0; i<=intervals.size()-1 && e==-1; i++){
            if(s==-1 && newInterval[0]<=intervals[i][1] && (i==0?1:newInterval[0]>intervals[i-1][1])) {s = i;}
            if(newInterval[1]>=intervals[i][0] && (i==intervals.size()-1?1:newInterval[1]<intervals[i+1][0])) {e = i;}
        }
        if(s==-1){
            intervals.insert(intervals.begin()+e+1, newInterval);
            return intervals;
        }
        cout<< s <<" "<< e <<endl;
        intervals[s] = {min(newInterval[0], intervals[s][0]), max(newInterval[1], intervals[e][1])};
        intervals.erase(intervals.begin()+s+1, intervals.begin()+e+1);
        return intervals;
    }
};

3.3.4. 380. Insert Delete GetRandom O(1)

key
- observation: random O(1) => vector, remove O(1) => hash map, combine those 2.

3.4. linked list

巧妙的构造虚拟头结点。可以使遍历处理逻辑更加统一。
灵活使用递归。构造递归条件，使用递归可以巧妙的解题。不过需要注意有些题目不能使用递归，因为递归深度太深会导致超时和栈溢出。
链表区间逆序。第 92 题。
链表寻找中间节点。第 876 题。链表寻找倒数第 n 个节点。第 19 题。只需要一次遍历就可以得到答案。
合并 K 个有序链表。第 21 题，第 23 题。
链表归类。第 86 题，第 328 题。
链表排序，时间复杂度要求 O(n * log n)，空间复杂度 O(1)。只有一种做法，归并排序，至顶向下归并。第 148 题。
判断链表是否存在环，如果有环，输出环的交叉点的下标；判断 2 个链表是否有交叉点，如果有交叉点，输出交叉点。第 141 题，第 142 题，第 160 题。

3.4.1. no.21 iterate & merge 2 list

careful:
- difference between while & for , while: more flexible, for: be very carefull when operating linked list since for have this delayed feature.

3.4.2. 355. Design Twitter

key
- observation: use priority queue& linked list

3.5. 2-pointer

双指针滑动窗口的经典写法。右指针不断往右移，移动到不能往右移动为止(具体条件根据题目而定)。当右指针到最右边以后，开始挪动左指针，释放窗口左边界。第 3 题，第 76 题，第 209 题，第 438 题，第 567 题，第 713 题，第 763 题，第 845 题，第 881 题，第 904 题，第 992 题，第 1004 题。

left, right := 0, -1

for left < len(s) {
    if right+1 < len(s) && freq[s[right+1]-'a'] == 0 {
        freq[s[right+1]-'a']++
        right++
    } else {
        freq[s[left]-'a']--
        left++
    }
    result = max(result, right-left+1)
}

快慢指针可以查找重复数字，时间复杂度 O(n)，第 287 题。
替换字母以后，相同字母能出现连续最长的长度。第 424 题。
SUM 问题集。第 1 题，第 15 题，第 16 题，第 18 题，第 167 题，第 923 题。

3.6. sliding window

双指针滑动窗口的经典写法。右指针不断往右移，移动到不能往右移动为止(具体条件根据题目而定)。当右指针到最右边以后，开始挪动左指针，释放窗口左边界。第 3 题，第 76 题，第 209 题，第 424 题，第 438 题，第 567 题，第 713 题，第 763 题，第 845 题，第 881 题，第 904 题，第 978 题，第 992 题，第 1004 题，第 1040 题，第 1052 题。

left, right := 0, -1
  
for left < len(s) {
    if right+1 < len(s) && freq[s[right+1]-'a'] == 0 {
        freq[s[right+1]-'a']++
        right++
    } else {
        freq[s[left]-'a']--
        left++
    }
    result = max(result, right-left+1)
}

滑动窗口经典题。第 239 题，第 480 题。

3.7. stack

括号匹配问题及类似问题。第 20 题，第 921 题，第 1021 题。
栈的基本 pop 和 push 操作。第 71 题，第 150 题，第 155 题，第 224 题，第 225 题，第 232 题，第 946 题，第 1047 题。
利用栈进行编码问题。第 394 题，第 682 题，第 856 题，第 880 题。
单调栈。利用栈维护一个单调递增或者递减的下标数组。第 84 题，第 456 题，第 496 题，第 503 题，第 739 题，第 901 题，第 907 题，第 1019 题。

3.7.1. 20. push & pop

3.7.2. xxx. Simplify Path

3.7.3. xxx. Basic Calculator

key
- observation: no need to keep all items since there are no */. keep a stack of signes and do +-.
  
  Example: 7 - ( 6 - 5 - ( 4 - 3 ) - 2 ) - ( 1 ) Result:+7-6 + 5+4 - 3 + 2-1

3.7.4.

careful
- can't use iterator to change value!

3.7.5. 402. Remove K Digits

key
- observation: result ith = smallest of[result i-1th:k-previous used]

3.7.6. 907 Sum of Subarray Minimums

key
- observation: result = sum(PLE(A[i]) * NLE(A[i])), so, stack.

3.7.7. 456 132 Pattern

3.7.8. Largest Rectangle in Histogram

key
- same as Sum of Subarray Minimums

3.7.9. 85. Maximal Rectangle

key
- same as Largest Rectangle in Histogram

3.7.10. Remove Duplicate Letters

key
- stack is used to simply keep a non-increasing array.

3.7.11. 975 Odd Even Jump

key
- dp provide us with a way of solving this: only we have to solve the next smallerst higher / next lartest smaller, use index stack!

3.7.12. 42. Trapping Rain Water

key
- observation: fill gap step by step: every gap is filled when left_bar < right_bar or left-1_bar < right_bar when encoutering higher bar, so a decreasing stack is needed.

3.8. heap

3.8.1. the skyline problem (i wouldn't say it's divide&concurd)

key:
- observation: first we need to observe that skyrim point is on every point when maximum height changes.
  
  thus, our priority is to efficiently update every maximum height.
- algorithm1: we can do linear check => O(n + m*p)
- algorithm2: we can do linear check with a heap so that we don't have to recheck the overlapping space, =>O(n+ m *log(m/2))
carefull
- == (?:)
int+1 => overflow
- try to make things easier => observation is the most important .

3.8.2. 719. Find K-th Smallest Pair Distance

key
- observation; this is an obvious heap problem, but to reduce complexity, you have to go from the most possible (th < k) elements to reduce times of poping, draw a map and use heap to find.

3.8.3. 295. Find Median from Data Stream

key
- observation: you want local maximum of lower half values and local minimum of higher half values.
  
  start => I want know the local maxnimum of lower half, but not knowing the upper half is impossible since sometimes we 'll need to shift big stuff down. noticing that shifting only concern with smallest item of upper half, so that's heap.

3.8.4. 407. Trapping Rain Water II

key
- observation: one points's element = min(largest surrounding set), a heap is used for the local min.
  
  so we keep min queue as surrounding set and move step by step by poping the smallest(why smallest? because smallest ensure that the updated stuff is valid).
  
  Proof: by setting the surrouding as peripheral, and updating each element making sure that the updated element is either filled or higher. The queue itself maintain the [smallest of largest wall] as it's top(). we prove it by deduction, if at i-1 th time it is the smallest of largest wall, then at i th time we pop the smallest and add it's peripherals, so for the unupdated elements which is at the queue's peripherals, the smallest either remain unchanged or is updated by the pushing operations, so updated operations either push > 1nd smallest at i-1 time, or == 1nd smallest at i-1 time, either way the smallest of largest wall remain true!.
  
  Note: that if trapping in 1D, the largest surrounding is equivalent to largest left + largest right, so a stack will suffice instead of maintaining a largest surrounding heap.

3.8.5. 786. K-th Smallest Prime Fraction

key
- observation: same as 719: find kth smallest in n sorted vectors.

3.8.6. 857. Minimum Cost to Hire K Workers

key
- observation: DP[i] means the optimal that pivot worker being i , the problem can reduce to min(dp[i]), DP[i] = pivot(wv/qv) * sum(qv+otherq). I first think that set all pivot workers and solve them separately, then I found that sum(otherq) overlaps between DP[i] and DP[i-1], since otherq = sum smallest of quality of K-1 items from (i-1:end), so DP[i] and DP[i-1] overlaps, sum(i:end) = if i > largest of i+1:end ? sum(i+1:end) : i + sum(i+1:end)-top() => use a heap to get top().
  
  IMG_4756

3.8.7. 778. Swim in Rising Water

key
- observation: when smaller numbers<=T are connected together => use a priority heap to do DFS.
  
  Proof: only condition that poping number > T is there's no other <= T left in heap, but no other <= T left in heap is that all heap is poped out to the edge since they are all connected.

3.9. deque

3.9.1. 239. Sliding Window Maximum

key
- observation: if we can keep the max order of current window, then on next level, we can do max stack(if we encounters a larger nums[i], then previous i-1:start that smaller than nums[i] won't work. so we can actually pop them out), so this is a decreasing stack problem. (why deque? because we need to pop the front as well when the front is out of the window)
  
  IMG_4560

3.10. map(hash table)

3.10.1. 975. Odd Even Jump

key
- map direct usage

3.10.2. Maximum Frequency Stack

key
- observation: separate problem to same frequency=> first we do pop on max_stack, if max_stack is gone, we do pop on max-1_stack, then it's natural to use multiple map_stacks to store both frequency and stack orders. You can consider freq as the first priority and stack order as the second.

3.10.3. 421 Maximum XOR of Two Numbers in an Array

key
- observation: for each bit, we want it from 31->1 since it requires the maximum. So, we see if there exists 2 elements that have different on first bit, then we move to second bit. One word, just think by endf

### 715. Range Module

key
- $O(logn)$ observation: Use a map to save the disjoint intervals. For example, m[left] = right means there is an interval [left, right).
  
  addRange: Apply removeRange(left, right) at first. Then add a new interval [left, right) in the map. Finally merge the previous interval and the next interval with [left, right) respectively, if they are adjcent.
  
  queryRange: Use m.upper_bound(left) to find the first interval i that i.left > left. Then we know prev(i).left <= left. If prev(i).right >= right, we should return true, otherwise false.
  
  removeRange: Find the last interval i that i.left < left. It is also the first interval which this delete operation may influence on. Then check all the intervals after iwhich intersects with [left, right). Apply delete operation for each interval.

3.10.4. 220. Contains Duplicate III

key
- $O(nlogn)$ observation: split the problem into result that start with index => pairs start with 0, start with n .... Then we apply sliding window technique, normally we find upper & lower bound
Note: lower_bound can be used to determine if there's element within range [a, b] => just seek for lower_bound(a) and go check if result <=b

3.10.5. Data Stream as Disjoint Intervals

key
- ;
Note: have to be carefull with lower_bound = begin() & upper_bound = end() situations.

3.10.6. LFU

key: here we notice the problem = choose least freq, at same freq use LRU. so it is natural to think that we should use map[freq, lrulist] (fm), then we want to record key=>freq(for determine which line) & value(for get), which is why we have m. then we notice that if fm changes, we have to scan through this shit, and it's position(iterator) does not change unless we use get(key)/put(key), which means we can record it using mIter to reduce time by adding mem.

class LFUCache {
public:
    int cap;
    int size=0;
    int minFreq=0;
    unordered_map<int, pair<int, int>> m; //key to {value,freq};
    unordered_map<int, list<int>>  fm;  //freq to key list;
    
    unordered_map<int, list<int>::iterator> mIter; //key to list iterator;
    
    
    LFUCache(int capacity) {
        cap = capacity;
    }
    
    int get(int key) {
        // cout<< "get" <<" "<< key  <<endl;
        if(!cap) return -1;
        if(m.count(key)){
            auto vf = m[key]; auto ite = mIter[key];
            m[key].second ++;
            fm[vf.second].erase(ite); fm[vf.second+1].insert(begin(fm[vf.second+1]), key);
            mIter[key] = begin(fm[vf.second+1]);
            if(fm[minFreq].empty()) minFreq++;
            return vf.first;
        }
        return -1;
    }
    
    void put(int key, int value) {
        // cout<< "put" <<" "<< key  <<" "<<value <<endl;
        if(!cap) return;
        if(m.count(key)){
            auto vf = m[key]; auto ite = mIter[key]; 
            m[key].second ++; m[key].first = value;
            fm[vf.second].erase(ite); fm[vf.second+1].insert(begin(fm[vf.second+1]), key);
            mIter[key] = begin(fm[vf.second+1]);
            if(fm[minFreq].empty()) minFreq++;
        } 
        else{
            if(size==cap){
                auto tobek = *rbegin(fm[minFreq]);
                m.erase(tobek);
                fm[minFreq].erase(--end(fm[minFreq])); 
                mIter.erase(tobek);
                size--;
            }
            
            m[key] = {value, 1};
            fm[1].insert(begin(fm[1]), key); 
            mIter[key] = begin(fm[1]);
            minFreq = 1;
            size++;
        }
        
    }
};

3.11. union find

灵活使用并查集的思想，熟练掌握并查集的模板，模板中有两种并查集的实现方式，一种是路径压缩 + 秩优化的版本，另外一种是计算每个集合中元素的个数 + 最大集合元素个数的版本，这两种版本都有各自使用的地方。能使用第一类并查集模板的题目有：第 128 题，第 130 题，第 547 题，第 684 题，第 721 题，第 765 题，第 778 题，第 839 题，第 924 题，第 928 题，第 947 题，第 952 题，第 959 题，第 990 题。能使用第二类并查集模板的题目有：第 803 题，第 952 题。第 803 题秩优化和统计集合个数这些地方会卡时间，如果不优化，会 TLE。
并查集是一种思想，有些题需要灵活使用这种思想，而不是死套模板，如第 399 题，这一题是 stringUnionFind，利用并查集思想实现的。这里每个节点是基于字符串和 map 的，而不是单纯的用 int 节点编号实现的。
有些题死套模板反而做不出来，比如第 685 题，这一题不能路径压缩和秩优化，因为题目中涉及到有向图，需要知道节点的前驱节点，如果路径压缩了，这一题就没法做了。这一题不需要路径压缩和秩优化。
灵活的抽象题目给的信息，将给定的信息合理的编号，使用并查集解题，并用 map 降低时间复杂度，如第 721 题，第 959 题。
关于地图，砖块，网格的题目，可以新建一个特殊节点，将四周边缘的砖块或者网格都 union() 到这个特殊节点上。第 130 题，第 803 题。
能用并查集的题目，一般也可以用 DFS 和 BFS 解答，只不过时间复杂度会高一点。

3.11.1. 751 Couples Holding Hands

key
- observation: nodes are cuples 1=>n/2, at [0,1], [2,3] we find if cuples are connected(not the same), if at those seats they do no not seat together, we put cuples A & B seet there connected. we out put the connected components K and N-K.
careful
- reserve = capacity, resize = size

3.11.2. 685. Redundant Connection II

key
- observation: use union find to efficiently find circle
  
  the only special case is case2 where you have to cut the last edge => we have to determine if there's other circle => we can't do circle detection on this edge.

3.11.3. 952. Largest Component Size by Common Factor

key:
- $O(n^2logM)$ observation: union find is obvious, use gcd.
- $O(n M^{1/2})$ observation: kind of like bucket sort, where you store all possible n connections instead of comparing them every time.

3.11.4. 803. Bricks Falling When Hit

key
- observation: 由0和1组成的矩阵，每次给定一个1敲掉，把敲掉后不与首行的1相连通的1一并都抹除。问每次敲一共会抹除多少元素。查与之连通的元素用union find。union find适合将两个component连起来，这里却需要把连起来的拆开，并查集并无法快速支持这样的操作，要尽量把敲掉替换成并查集擅长的union操作。因此把敲掉看作倒着的补齐操作，每次补上元素后新增加与首行1相连的元素即敲掉元素所失去的元素。并查集还有个常用的小优化，即生成一个dummy src连接所有的首行1形成一个大component，这样只需要查一次src的size就知道所有与首行1连通的元素数目。

3.11.5. 928. Minimize Malware Spread II

key
- $ O(n^2)$ observation: same as 803 in some way, start from no hits and add them separately, count the consequencies when hitting happens.
- optimization: at first I thought i should connect initials one by one with other initials connected, actually only need to connect initials with other initials unconnected

3.11.6. 924. Minimize Malware Spread

key
- observation, same as 928, a little adjustment, contraints become more strict: First, a node have to connect to no other initials, Second, a node have to connect to no other initials infected fields.

3.11.7. 128. Longest Consecutive Sequence

key
- $O(n^2)$ observation: do union find on nodes;
- $O(n)$ observation: do union find on nodes if nodes exist.

3.11.8. 839. Similar String Groups

key
- $O(n^2 *m)$:
- $O(n*m^2)$:

3.11.9. Most Stones Removed with Same Row or Column

key
- $O(n^2)$ observation1: connect the stones which is pretty much straight forward.
- $O(n)$ obsevation2: intuition: node is only concerned with its coordinates. so connect the coordinates ?? which is tricky and not straight forward. don't need to know the exact parents, just need to know to component counts.
  
  Proof: a node is connected to another if and only if it's coordinate is connected, so we if 3 groups of node are connected, then there must exists 3 groups of coordinates.

### regionsBySlashes

key
- observation: key point of this problem is how to separate node easily, first thought is consider '/' as 0,1 and '\' as 3,4 the point is you have to look ahead what's adj to determine what to merge
- optimization: split into 4 nodes, / will different from connecting the same nodes different parts and since comparatively positions are fixed, don't have to look ahead which is very tedious work.

3.12. bt

3.12.1. Binary Tree Postorder Traversal

key:
- stack implement traversal is all the same(DFS), post/pre/mid is just the time to push in value

3.12.2. 834. Sum of Distances in Tree

key
- observation: RES[i] = sum of all before[i]
- optimization: compute RES[root] & RES[i] = RES[i->parent] + countbeforei - countafteri.
  
  Note: you can see that we don't need to keep vector of all sum, since it's all 1s, we only need the counting of before and sum of vector.

3.12.3. 236. LCA

key
- observation: ez dfs

3.12.4. 106. Construct Binary Tree from Inorder and Postorder Traversal

key

observation: you can see that postorder cut the tree by right sub and midorder have the advantage of cutting the tree to left & right.

class Solution {
    int start;
public:
    TreeNode* merge(TreeNode* r1, TreeNode* r2, int a){
        auto merge = new TreeNode(a); merge->left = r1; merge->right = r2;
        return merge;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder, int left, int right) {
        if(left>right) {return nullptr;} if(left==right) {new TreeNode(inorder[right]);}
        int pivix = postorder[start--]; auto f = find(inorder.begin(), inorder.end(), pivix)-inorder.begin();
        
        auto g = buildTree(inorder, postorder, f+1, right), i = buildTree(inorder, postorder, left, f-1);
        return merge(i, g, pivix);
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        start = inorder.size()-1; if(start==-1) return NULL;
        return buildTree(inorder, postorder, 0, start);
    }
};

3.12.5. 897. Increasing Order Search Tree

key

observation: dfs(tree, node) = return ordered tree & tree 右端接上 node

def increasingBST(self, root, nex = None):
  if not root: return nex
  left = increasingBST(root.left, root)
  root.left = None 
  root.right = increasingBST(root.right, nex)
  return left

and proof goes to edges cases 1->2/ 2->1 / 1 ->none, check all edge cases then we have it proofed.

3.12.6. 979. Distribute Coins in Binary Tree

key
- observation: pick all node with coins more than 1 and do bfs（WRONG）
- observation: dfs(node) = number of coins needed/left, do dfs(node) and add all abs from left & right which means up & down delivers
  1
  2
  3
  4
  rl, left = dfs(root.left)
  rr, right = dfs(root.right)
  res = abs(left) + abs(right) + rl + rr
  return res, root.val + left + right - 1
  Proof: res = 在假设硬币都够的情况下满足该子树都ok所需要传递的硬币费用=abs(left) + abs(right)+rl+rr, 如果孩子缺钱，那么从父母给钱是最快的，所以需要先给钱（abs），再加上满足子树所需操作（rl）；如果孩子多钱，意味着该孩子下面全都满足一个硬币，所以给父母是必须的（abs），再加上满足子树所需操作（rr）。归纳法到最后证明最简单二叉树也是满足的。事实上bfs也是这么做的，因为bfs只能往下传/往上传，而且bfs也不对，因为该节点必须先满足自己的子树都ok才行。

3.13. bst

3.13.1. 315. Count of Smaller Numbers After Self (from D&C)

key
- observation: this is actually from D&C algorithm2:
  
  => cur[i] = smaller[i+1:end] => insert cur[i] into [i+1:end] and see how many is smaller.(this is usage of BST)

3.13.2. 450 delete BST

key

observation:

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root==null) return null ;
        if(root.val>key) root.left=deleteNode(root.left,key);
        else if(root.val<key) root.right = deleteNode(root.right,key);
        else {
            
            if(root.left==null) return root.right;
            if(root.right==null) return root.left;
            
            TreeNode rightmin = findmin(root.right);
            root.val = rightmin.val;
            root.right = deleteNode(root.right,root.val);
        }
        return root;
    }
    private TreeNode findmin(TreeNode root){
        while(root.left!=null)
            root=root.left;
        return root;
    }

careful
- avoid reference return between functions, do it in one function if possible.

3.13.3. 222. Count Complete Tree Nodes

key
- $O(n)$ observation: BFS
- $O(log(n)^2)$ observation: divide tree into 2 parts, at least one part is perfect, so basically
  
  count = count(left or right) + full tree.

3.13.4. BST iterator

key

observation: instead of doing BST recursive visits, we can store BST in stack

int next() {
  TreeNode *tmpNode = myStack.top();
  myStack.pop();
  pushAll(tmpNode->right);
  return tmpNode->val;
}

void pushAll(TreeNode *node) {
  for (; node != NULL; myStack.push(node), node = node->left);
}

Proof: at node i we prove the next node is it's next, if no right=> next is parent, if right => next is right sub tree's leftiest. or you can simply think of straps of nodes

3.13.5. 108. Convert Sorted Array to Binary Search Tree

key

observation: thinking from depth = 0->4, and you can see that it is guaranteed that layer i can be split into layer i-1 by choosing the root = len(nums)/2, so there's that.

# 0 1 
# 1 => 1        1 
# 2 => 0/1 +1  2 3 
# 3 => 2/2 2/3 3/3  5 6 7 
# 4 => 5/5 5/6 =>7/7   11 12 13 14 15  
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if not nums: return None
        root = TreeNode(nums[int(len(nums)/2)])
        root.left = self.sortedArrayToBST(nums[:int(len(nums)/2)])
        root.right = self.sortedArrayToBST(nums[int(len(nums)/2)+1:])
        return root

3.13.6. 109. Convert Sorted List to Binary Search Tree

key

observation; we construct bst in in-order, so we can say that the root of left & right will appear after access of left subtree(当使用数组的时候，我们直接取mid就行，如果用链表，就要把所有经过的左子树节点.next就是root了z)

def dfs(head, start, end):
    
    mid = start + int((end-start)/2);
    if start > end: return None;
    
    l = dfs(head, start, mid-1);
    root = TreeNode(self.cur.val);
    self.cur = self.cur.next;
    r = dfs(self.cur, mid+1, end);
    root.left = l; root.right = r;
    return root;

3.14. segment tree

线段数的经典数组实现写法。将合并两个节点 pushUp 逻辑抽象出来了，可以实现任意操作(常见的操作有：加法，取 max，min 等等)。第 218 题，第 303 题，第 307 题，第 699 题。
计数线段树的经典写法。第 315 题，第 327 题，第 493 题。
线段树的树的实现写法。第 715 题，第 732 题。
区间懒惰更新。第 218 题，第 699 题。
离散化。离散化需要注意一个特殊情况：假如三个区间为 [1,10] [1,4] [6,10]，离散化后 x[1]=1,x[2]=4,x[3]=6,x[4]=10。第一个区间为 [1,4]，第二个区间为 [1,2]，第三个区间为 [3,4]，这样一来，区间一 = 区间二 + 区间三，这和离散前的模型不符，离散前，很明显，区间一 > 区间二 + 区间三。正确的做法是：在相差大于 1 的数间加一个数，例如在上面 1 4 6 10 中间加 5，即可 x[1]=1,x[2]=4,x[3]=5,x[4]=6,x[5]=10。这样处理之后，区间一是 1-5 ，区间二是 1-2 ，区间三是 4-5 。
灵活构建线段树。线段树节点可以存储多条信息，合并两个节点的 pushUp 操作也可以是多样的。第 850 题，第 1157 题。

3.14.1. 1157. Online Majority Element In Subarray

key
- observation $O(logn)$ : actually not a good way to use moore-vote + segment tree since, moore-vote requires threshold to be met, however we do not know if it is met, so we have to do additional check (e.g. a binary search on indexes) which makes it too chunky.

3.14.2. 699 Falling Squares

key
- $O(logn)$ observation: discrete max_segment_tree problem, ez.

3.14.3. 850. Rectangle Area II

key
- $O(nm) $ observation: just set them all
- $O(nm ) $ observation: discretion, decrease complexity by cutting into rectangles instead of node by node.
- $O(n logn)$ observation: discretion + update using sum Segment_tree

3.14.4. 732. My Calendar III

key
- $O(t^2)$ solution: step by step discretion .

3.15. Trie

3.15.1. 1178. Number of Valid Words for Each Puzzle

key

observation: find if string in a set of strings,

class Solution {
    struct TrieNode{
        int countEnd;
        TrieNode* children[26];
        TrieNode() {
            countEnd = 0;
            memset(children, 0, sizeof(TreeNode*)*26);
        }
    };
    TrieNode trie;
    
    void insert(int countChar[26]) {
        TrieNode * currNode = & trie;
        for (int i = 0; i < 26; i++) {
            if (countChar[i] == 1) {
                if (currNode->children[i] == nullptr)
                    currNode->children[i] = new TrieNode();
                currNode = currNode->children[i];
            }
        }
        currNode->countEnd ++;
    }
    
    void buildTrie(vector<string> & words) {
        int countChar[26];
        for (int i = 0; i < words.size(); i++) {
            memset(countChar, 0, sizeof(int)*26);
            string & w = words[i];
            for (auto c: w) { countChar[c-'a'] = 1; }
            int count = 0;
            for (int i = 0; i < 26; i++) { count += countChar[i]; }
            if (count > 7) continue;
            insert(countChar);
        }
    }
	
	int search(TrieNode* node, string & p, int idx, char firstChar, bool metFirst) {
        int res = 0;
        if (node->countEnd > 0 && metFirst) {
            res += node->countEnd;
        }
        for (int i = idx; i < p.length(); i++) {
            if (node->children[p[i]-'a'] != nullptr) {
                res += search(node->children[p[i]-'a'], p, i+1, firstChar, metFirst || (p[i] == firstChar));
            }
        }
        return res;
    }
public:
    vector<int> findNumOfValidWords(vector<string>& words, vector<string>& puzzles) {
        buildTrie(words);
        vector<int> res;
        for (int i = 0; i < puzzles.size(); i++) {
            char firstChar = puzzles[i][0];
            sort(puzzles[i].begin(), puzzles[i].end());
            int cnt = search(&trie, puzzles[i], 0, firstChar, false);
            res.push_back(cnt);
        }
        return res;
    }
};

3.15.2. 687. Longest Univalue Path

key
- observation: DP[node] = longest path from node \[ DP[node] = max(\\DP[left]if(v==v->left),\\ DP[right]if(v==v->right) ) \]

3.15.3. 987. Vertical Order Traversal of a Binary Tree

key
- observation: use map ...

3.15.4.

key

observation: searching n in 1 tree is trivial, searching 1 in n tree is the right solution, and you can see that the only condition that we get res = 1 is we finish the way alone the pattern&word, is that we finish both lower and upper, and lower can be more, but upper is exactly the same.

void search(TrieNode* root, string & p, vector<bool>& res, int start) {
    if(!root) return;
    
    int index = islower(p[start])?p[start]-'a':p[start]-'A'+26;
    if(start!=p.length()){
        search(root->children[index], p, res, start+1);
        for(int j=0; j<=25; j++)
            if(j!=index) search(root->children[j], p, res, start);
    }
    
    if(start==p.length()) for(int j=0; j<=25; j++){
        if(root->_countEnd!=-1) res[root->_countEnd]=true;
        search(root->children[j], p, res, start);
    }

}

3.15.5. 692. Top K Frequent Words

key
$O(n+k)$ observation: It is a must-have to map a word to its frequency. Since we aim to get k words with largest frequency, we have to map frequency to words and sort frequency decreasingly. Heap or TreeMap achieve that with O(n log k) time complexity, however, we could do better using Bucket Sort that takes O(n + k) time complexity for n is number of elements and k is number of buckets. Since we have to output words lexicographically, we take advantage of Trie for it has no sorting costs. That is, we build a trie consists of all words within the same bucket. And we apply DFS to traverse the trie and add words we met to the result list one by one. Finally, we go through buckets from tail to head until we get top K frequent words.

3.15.6. 745. Prefix and Suffix Search

key
- observation: a seriously complicated trie tree problem, the DFS is serious mind-melting

3.16. graph

usage:
- dij is a special form of DP, DP[set()] means that value in set() is all updated and DP[set()]->...DP[{start}], so dij is actually building this DP bottom up by adding an element into set at each step.
- topo_sort can efficiently compute max_height

3.16.1. 882. Reachable Nodes In Subdivided Graph

key
- observation, the problem actually what to know K-min_dist(start, i) for every i, so actually a dij problem.
  
  Note: that it is equavalent to use a max queue and store K-min_dist, one can prove that the poping sequence is the same as min queue or directly prove this problem as the same as Dij.

3.16.2. 212. Word Search II

key
- observation: this is a typical dfs problem where we can use trie to expedite the process. tree problem
Note: For Trie, 26 pointers to point the sub-strings and a bool leaf to indicate whether the current node is a leaf (i.e. a string in words) and also idx is used to save the index of words for the current node. For DFS, just check if the current position is visited before (board[i][j]=='X'), if so, return, check if there is a string with such prefix (nullptr == root->children[words[idx][pos]-'a']), if not, return; otherwise, check if the current searched string is a leaf of the trie (a string in words), if so, save it to res and set leaf of the trie node to false to indicate such string is already found. At last, move to its neighbors to continue the search. Remember to recover the char [i][j] at the end.
careful
- be sure to use & when necessary! since not using & will copy this fucker and slow the code down!!

3.16.3. 399. Evaluate Division(floyd)

key
- observation: variation of floyd=>

3.16.4. 1203. Sort Items by Groups Respecting Dependencies(topo)

key
- observation: topo sorts

3.16.5. 1042. Flower Planting With No Adjacent

key
- observation: since only 3 edges are connected so the choose is easy, anything is ok
- optimization: if more than 3 edges are connected, sort the order of which gardens to plant flowers in by the number of edges it is connected to:
  1
  sortedEdges = sorted(((len(g[x]), x) for x in g), reverse = True).

3.16.6. 802. Find Eventual Safe States (find circles)

key:
- observation: need to find circles. 3 conditions below
  
  Untitled-22

3.16.7. 785. Is Graph Bipartite

key
- observation: separate the problem into k components, and do dfs on each of them.

3.16.8. 310. Minimum Height Trees

key
- $O(n)$ observation: do bfs on leaves, and the last that survives are the possible roots. So basically in the end, the nodes in the queue would be connected to no other nodes but each other.
  
  Lemma: there can't exists more than 2 on the last layer, so the it's either 1 or 2, so we can output the nodes with degrees = 0.
- optimization: you can either use visited set(which is slow) / remove the edge when used.
  
  Untitled-28

3.16.9. Euler path

key
- greedy observation: 因为存在欧拉通路（权都为偶数），所以可以以欧拉通路的遍历方式做遍历，然后

3.17. divide & concur (basic bottom-up)

3.17.1. 240. find(i, j) = find(i-1, j) || find(i, j+1)

key
- observation: find propagation function between problem & subproblems

3.17.2. 215. Kth Largest Element in an Array

key
- observation: we can sub this problem by => if we need to find the kth largest the problem becomes sort(k) , we know that we have all k-1 smaller element on its left ( e,g. 5 6 4(*) 3 1 2 if we want the 3rd largest) so we don't acctually care about the order of left of 4. so the subproblem can be sort(k-1), k-2 ... 1 largest. The hard point is that we don't know the kth partition pivix, so we can only guess the pixiv, for example if we choose the last element of array, we can use std::partition to solve the subproblem. so we random solve $sort(m) => sort((m-1)/2) or sort(random(n<n)) $
- alternative: insert heap

3.17.3. 932 beautiful array

key
- observation: from odd & . => $array(n) = (array((n+1)/2)*2-1) +(array(n/2)*2)$

3.17.4. Count of Range Sum

key
- observation: when left of merge_vector and right of merge_vector is sorted will help with the searching like in this case is nums[i] - nums[j], sorted left and sorted right will only cost O(n) to merge search.
  
  range sum => prefix[i] - prefix[j]. Think about merge and sort, we can split the prefix into 2 => [13,21,3,123,] [1,312,3,123,12,] and if we computed count(left) + count(right) + count(in between), it is O(n2), however if we sort the array along => O(nlogn + n(merge)) . done. same if we split into [n-i] [i], we use insert sort instead of merge sort. => O(nlogn + n2)
careful
- == (?0:1) add parathesis
- notice when empty

3.17.5. 493. Reverse Pairs

key
- observation1: $rev(i) = res(i-1) + c$, tried red-black tree => O(n * n)(worst case) but TLE. or we can try BIT whose worst case is O(n logn) , by using BIT we insert the index of element and sum of BIT become the num of element satisfying the condition.
- observation2: $rev(i) = rev(i/2)+rev(i/2+1)+c$, by this propagation equation we can sort the array along the subproblem, by sorting the array we can use 2 pointer trick to make it linear => O(n)

3.17.6. 60. Permutation Sequence

key
- observation: add k/(n-1)! th element to the front then it becomes a subpermutation without that element, use an array to store all usable elements.

3.17.7. Can I Win

key
- observation: DFS[vector, int] = if this situation will succeed.

3.18. dynamic programming

3.18.1. 303 sum(i, j)

key
- observation: use down-top & subproblem: sum(i, j) = sums[j] - sums[i], which means n subproblems. note that: dynamic programming may seem not necessary in this senecio, but dp not only save time on 1 time calling, but saving time on multiply calling as well;
- alternative: top-down is not neccsary in this.

3.18.2. 198 maxsolution(i)

key
- observation: use down-top: robs[i] = max(robs[i-1], robs[i-2] + nums[i-1]);
- alternative: can use more variables (2 pointer ) to record delay : [i-2] and [i-1] (not preferred)
  1
  2
  3
  ninc = ex + it;
  ex = max(inc, ex);
  inc = ninc;
  is same as
  1
  robs[i] = max(robs[i-1], robs[i-2] + nums[i-1]);
- alternitive: tried top-down, so fucking memory-consuming and hard to write, make sure that use smallest data as possible, such as <vector, i> can replace
carefull
- int are init as 0; char are init as unknown. memset(robs,-1,sizeof(robs));
- remember that the index difference (offset = 1) of array and memory maxsolution(i)

3.18.3. 53. maxsum(i, j)

key:
- observation: use subproblem: maxsum(i, j) = max(local(0~i)) local(i) = max(local[i-1], local[i-1]+xx), n subproblems, o(n).
- equivalent implement: math trick: think about the features about problem before solving it: in this problem, you can see if optimal = sum(i, j) that we must have every sum(i-k, i) < 0. therefore our priority is to set the starting point at i and it will turn to a O(n). so we only have to set sum = 0 if we sum <0 (which means start over from a new point) then it suffices to prove that the algorithm will let us start at i which yields the optimal.
- more advaned algorithm: use $ms=max(sum(j)-sum(i))$ so we save the $min(k) k<i $ during the loop and it's done.... so easy. this solution have nothing to do with dp.

3.18.4. 392. max(i, j)

key:
- obervation: can't use subproblem, so it have to be a 2-dim array
- improve: use space saving tech!! 2-dim -> 2*1-dim
careful:
- i = 0/ j=0
- copy 2 array & conditions
- the change of prop equation
- no assignment in if.

3.18.5. 91 max(i)

key:
obervation: consider all possible outcomes
carefull:
- "0" and 0

3.18.6. 523. Continuous Subarray Sum

key:
- obervation: boring & tedious

3.18.7. 1191 K-Concatenation Maximum Sum

key:
- obervation: observe this string first. 从大到小思考，划清界限：比如在这里设用到i个方块里面的数字。那么i=0到k，k到2的情况都是等价的，可以证明他们必然终止于同一点。所以只需要考虑max1, max2, max2+(k-2)sum,然后max2 >= max1, 所以解为max(m2, m2+(k-2) sum)。这道题的动态规划比较隐蔽，而且没有复杂的规约式子,maxj = max(j-1) + max(0, sum). 所以需要好好思考。

3.18.8. 514. Freedom Trail

key
- observation: separate the problem to sub[i-1]+problem[from i-1 to i] = sub[i]. matrix[keysize][ring size], and matrix[i][j] means that key <=i 's smallest route on ring[j].
  
  $$ \[\begin{equation} matrix[i][j]= \left\{ \begin{array}{**lr**} min_k(matrix[i-1][k] + distance[k\to j]) & \text{if k is not empty} \\ INT\_MAX & \text{if ring[j] != key[i]} \end{array} \right. \end{equation}\] $$
carefull
- init size of vector
- iteration i & j don't mess them up
- don't mess up the parameters

3.18.9. 903. Valid Permutations for DI Sequence

key
- observation: separate the problem to sub[i-1] + xxx = sub[i]
  
  （1） we think about this problem from i-1 to i: that if we set DL, how about DLD?
  
  （2） we think of matrix[i][j] means the i th element is the jth largest among all string, then we can use DL to indicate the [i+1][j] from ith, that if D=> we add matrixi[j] to all matrix i+1[<j], but here's the problem we don't have the ability to solve the duplicate issue.
  
  （3） so we improve 1) by setting j = sizeofstring+1-i and contains the jth largest of the rest of string. the reason we do this is we don't have to worry about duplicate, since the i and j suffices m[i][j] = jth ... = sum of all m[i-1] ; and the final matrix[size][1] = size*(size-1)*(size-2) ... = all possible, so we can choose who to pick from level i-1 only by "DL" string. And we can see that setting in 1) do not satisty this sum of propagation which means we have to choose who to sum up not only from the string but also considering whether there is duplicated element, which is a big problem.
  
  \[ \begin{equation} matrix[i][j]=\left\{ \begin{array}{**lr**} \sum_{k=j+1}^{size+2-i} matrix[i-1][k] & \text{if string[i-2]='D'} \\ \sum_{k=1}^{j} matrix[i-1][k] & \text{else} \end{array} \right. \end{equation} \]
- algorithm2:
  
  （0） we get 0~i-1 permutation(i-1 substring), we do sth to get i permutation(i substring)
  
  let's say dp[i][j] represents the number of permutation of number 0, 1, ... , i which ends with j. Also, it represents the answer of s.substring(0, i) which ends with j . this actually stems from the brilliant idea that we first use 0 to i-1 permutation and add 1 to those >= j where j is the the end of i permutation. This works because the only cases where +1 will destroy the order is when j = k+1 and permu(i) - permu(k) = +-1 (e.g. 23) and by adding >= j, the order of 23 will not change, therefore it's safe to add the 1 to i-1 permutation and get i permutation. therefore we have the equation below \[ dp[i][j]=\left\{ \begin{array}{**lr**} sum(dp[i - 1][0], dp[i - 1][1], ... , dp[i - 1][j - 1]). & \text{s.charAt(i - 1) == 'I': I}\\ sum(dp[i - 1][j], dp[i - 1][j + 1], ... , dp[i - 1][i - 1]). & \text{s.charAt(i - 1) == 'D':} \end{array} \right. \] （1） the above 2 algorithms stems from the same D&C intuition, but they construct by different ways algorithm1 construct a string by directly saying that what should be the end of the first elements of the final string. algorithm2 construct a string with a subset of permutation however following the same rule and construct a larger string by that. algorithm1 is more intuitive, algorithm2 takes more time to think about and prove it's correctness.

3.18.10. 312. Burst Balloons

key:
- observation : i-1 and i doesn't work. start:i-i i i+1:end work in this case
  1. set matrix[i][j] = from [i to j] optimal sequence when i-1 and j+1 are not bursted yet.
  2. we can get the following equation \[ d[i][j] = \max \limits_{k \in[1,n-2]} d[i][k-1] + d[k+1][j] +s[i]s[k]s[j] \] Note: this seems quite easy but it's not intuitive, in order to get this equation we have to assume k is the last to burst. the naive thought would be s[i-1] => s[i] but this is too complicated, so [i][j-1] and [j][i] will it work? if j-1 and j is connected, this is fucked up since [i:j-1] is affected by [j:end], to make separate the problem , we have to make them independent, which means [i:j-1] have to be secured by a fixed j that have nothing to do with the right part which leaves us no choice and have to choose j as a fixed ballon. In the mean time, j has to be fixed since the right of j requires the same as well. So j is fixed all the time which means it is the last one to burst, only by this assumption, we can separate the problem into 2 independent subproblems. And we have to keep in mind that we have many choices as fixed j, we choose the maximum.

3.18.11. 44 wildcard matching

key

observation: dp[i][j] means validity with [0,i] & [0,j] , and that we can sub this problem using a 2 pointer, mind that below is a simplified version of dp, the original dp of condition2 is dp[i][j] = OR_all_i-k,j , since i-1,j itself equals OR_all_i-1-k,j, we only need to OR dp_i-1,j => simplifies the problem \[ \begin{equation} dp[i][j]=\left\{ \begin{array}{**lr**} dp[i-1][j-1] & \text{if s[i]==p[j] or p[j] =='?'} \\ dp[i-1][j] || dp[i][j-1] & \text{if p[j] == '*'} \\ false & \text{else} \end{array} \right. \end{equation} \]

class Solution:
    def isMatch(self, s, p):
        dp = [[False for _ in range(len(p)+1)] for i in range(len(s)+1)]
        dp[0][0] = True
        for j in range(1, len(p)+1):
            if p[j-1] != '*':
                break
            dp[0][j] = True
                
        for i in range(1, len(s)+1):
            for j in range(1, len(p)+1):
                if p[j-1] in {s[i-1], '?'}:
                    dp[i][j] = dp[i-1][j-1]
                elif p[j-1] == '*':
                    dp[i][j] = dp[i-1][j] or dp[i][j-1]
      return dp[-1][-1]

3.18.12. 10 Regular Expression Matching

key

observation:

We define dp[i][j] to be true if s[0..i] matches p[0..j] and false otherwise. The state equations will be:

\[ \begin{equation} dp[i][j]=\left\{ \begin{array}{**lr**} dp[i - 1][j - 1] )& \text{if(s[i] == p[j] || p[j] == '.')} \\ (dp[i - 1][j]\&(s[i] == p[j - 1] || p[j - 1] == '.')) || dp[i][j-2]& \text{if p[j]='*'} \\ false \end{array} \right. \end{equation} \]

class Solution:
    def isMatch(self, s, p):
        dp = [[False for _ in range(len(p)+1)] for i in range(len(s)+1)]
        dp[0][0] = True
   
        for i in range(0, len(s)+1):
            for j in range(1, len(p)+1):
                if i and p[j-1] in {s[i-1], '.'}:
                    dp[i][j] = dp[i-1][j-1] 
                elif p[j-1] == '*':
                    dp[i][j] = dp[i][j-2] or (i and dp[i-1][j] and (s[i-1] == p[j-2] or p[j-2] == '.'))
                    
                print(i, j, dp[i][j])
        return dp[-1][-1]

3.18.13. 140. Word Break II

key
- $O(2^n )$ observation: DFS is obvious, level_i = fixed first i words. but we can see that there are overlapping problems, so we can use DP to accelerate process.
- $O(2^ n)$ algorithm2: top down DP, top town DP is most similar to DFS, but to use a map(prefer unordered for performance purposes) saving the results will make it faster.
- $O(2^n)$ algorithm3: bottom up DP, bottom up DP in this problem is not preferred since we have propagation function below, use DP[i] to indicate results for [0,i] : \[ DP[i] = combine(DP[j],s[j+1:i]) \text{if s[j+1:i] $ \in$ wordset } \] so implement this b-u DP, we'll have to find all possible problems.

3.18.14. 691. Stickers to Spell Word

key :

$O(2^{s(target)}*s(sticker))$ observation: bottom-up so fucking hard! observe this problem, you can the following dp equation: if DP[i] indicate minimum of the ith permutation subset we can see that: since k<i, so every j>i, DP[j] depends on DP[i], so we acctually can iterate from i = 0 => $2^n$, after step i, DP[i+1] is uptodate, so we can derive from here that DP[m-1] is uptodate. \[ \begin{equation} dp[i]=\left\{ \begin{array}{**lr**} (DP[k]+1) & \text{k $\in$ set is possible position k union sticker=i} \\ INTMAX& \text{if set_size=0} \end{array} \right. \end{equation} \]

class Solution {
public:
    int minStickers(vector<string>& stickers, string target) {
        int n = target.size(), m = 1 << n; // if target has n chars, there will be m=2^n-1 subset of characters in target
        vector<uint> dp(m, -1); // use index 0 - 2^n-1 as bitmaps to represent each subset of all chars of target
        dp[0] = 0; // first thing we know is : dp[empty set] requires 0 stickers,
        for (int i = 0; i < m; i++) { // for every subset i, start from 00000...(emptyset) to 111111...(the target)
            if (dp[i] == -1) continue;
            for (string& s : stickers) { // try use each sticker as an char provider to populate a super-set of i,
                int sup = i;
                for (char c : s) { // to do that, for each char in the sticker, 
                    for (int r = 0; r < n; r++) {
                        if (target[r] == c && !((sup >> r) & 1)) { // try apply it on a missing char in the subset of target
                            sup |= 1 << r;
                            break;
                        }
                    }
                }
               // after you apply all possible chars in a sticker, you get an superset that take 1 extra sticker than subset
               // would take, so you can try to update the superset's minsticker number with dp[sub]+1;
                dp[sup] = min(dp[sup], dp[i] + 1); 
            }
        }
        return dp[m - 1]; // and the ultimate result
    }
};

Note: the hard part of this bottom-up implementation is that you don't know the exact thing to update=> but the algorithm implies that after ith time, DP[i+1] is updated, so you can see that is the hard part.

algorithm2: top-down

class Solution {
public:
    int minStickers(vector<string>& stickers, string target) {
        int m = stickers.size();
        vector<vector<int>> mp(m, vector<int>(26, 0));
        unordered_map<string, int> dp;
        // count characters a-z for each sticker 
        for (int i = 0; i < m; i++) 
            for (char c:stickers[i]) mp[i][c-'a']++;
        dp[""] = 0;
        return helper(dp, mp, target);
    }
private:
    int helper(unordered_map<string, int>& dp, vector<vector<int>>& mp, string target) {
        if (dp.count(target)) return dp[target];
        int ans = INT_MAX, n = mp.size();
        vector<int> tar(26, 0);
        for (char c:target) tar[c-'a']++;
        // try every sticker
        for (int i = 0; i < n; i++) {
            // optimization
            if (mp[i][target[0]-'a'] == 0) continue; 
            string s;
            // apply a sticker on every character a-z
            for (int j = 0; j < 26; j++) 
                if (tar[j]-mp[i][j] > 0) s += string(tar[j]-mp[i][j], 'a'+j);
            int tmp = helper(dp, mp, s);
            if (tmp!= -1) ans = min(ans, 1+tmp);
        }
        dp[target] = ans == INT_MAX? -1:ans;
        return dp[target];
    }
};

3.18.15. 975. Odd Even Jump

key
- observation dp_h[i] = success or not if go higher at i
  
  \[ \begin{equation} res= \sum_{i=1}^{n}dp_h[i] \\ dp_h[i]=dp_l[nexthigher(i)] \\ dp_l[i]=dp_h[nextlower(i)] \end{equation} \]
  
  Note: that dp[i] depends on higher i so, we go from higher to lower .

3.18.16. 871. Minimum Number of Refueling Stops

key
- observation: dp[t] means the furthest distance that we can get with t times of refueling.
  
  So for every station s[i],if the current distance dp[t] >= s[i][0], we can refuel: dp[t + 1] = max(dp[t + 1], dp[t] + s[i][1]) In the end, we'll return the first t with dp[i] >= target, otherwise we'll return -1. \[ dp[i][j]= max(dp[i][j-1],dp[i-1][j-1]+fuel[j]) \text{ if dis[j]<=dp[i]} \] Note: that we actually go station by station, at each station we update the all possible largest outcome by taking all -> none. At a new station, largest dp[i][j] is either the i largest of 1:j-1 or i-1 largest of 1:j-1 and take station j. by seeing that dp[i][j] is only concern with 2 element on the previous row, we can reduce the matrix to an row and set an update sequence to make sure it is equivalent to matrix.
  
  IMG_3698
careful
- don't use auto=size()

3.18.17. 818. Race Car

key
- observation: dp[i] means the least number of target i \[ dp[i] = min(dp[2^n-1-i] + steps, dp[i-2 ^{n-1}+2 ^{m}]+steps. \text{ n=floor(log2(i))} \] ok, so we go like [AAAAR][AAAR] and number of A could be zero so we include the double turning situation. the nA could be anything from $2 ^{m}-1$, we have to do trimming. So the Lemma here is for i, it has to include either $2 ^{n}-1 $ or $2 ^{n-1}-1$, the former is easy to prove, however to prove the latter is hard.
  
  Note: The observation is that for i that $ 2 ^{m-1}-1 +2^{m}-1 +1i 2 ^{m}-1+2 ^{m+1}-1$ , $2 ^{m}-1$ will always appear on the optimal answer. So you can see it's either the 2 options given above (e.g. for i > 2**4 and i < 2^5, it's either 15 or 31)
  
  IMG_6261
  
  Note: even if can't come up with this optimization, the obvious thoughts will work => go F from 0 to n-1 and go back for less.
careful
- (1<<(sss))
- set the first dp not min, if you can't assign global vector. or you can assign it in main.

3.18.18. 630. Course Schedule III

key

observation: same as 871.

class Solution {
public:
    int scheduleCourse(vector<vector<int>>& courses) {
        sort(courses.begin(), courses.end(), [](vector<int>& a, vector<int>& b) {return a[1] < b[1];});
        int n = courses.size(); vector<int64_t>dp(n, INT_MAX);
        for(int i=0; i<=n-1; i++){
            for(int j=i; j>=0; j--){
                if(i==0) {dp[j] = courses[0][0]<=courses[0][1]?courses[0][0]:INT_MAX; continue;}
                if((j==0?0:dp[j-1])+courses[i][0]<=courses[i][1]){dp[j] = min(dp[j], (j==0?0:dp[j-1])+courses[i][0]);}
                cout<< i <<" "<< j <<" "<< dp[j]   <<endl;
            }
        }
        int i=0; for(; i<=n-1; i++) if(dp[i]==INT_MAX) break;
        return i;
    }
};

careful
- ((1==?):0:1)

3.18.19. Jump Game II

key
- observation: same as 871

3.18.20. 1235. Maximum Profit in Job Scheduling

key
- observation O(n3): \[ DP[i][j] = DP[q<i][j-1]... \]

algorithm2 O(n2): DP[i] means DP max taking i \[ DP[i] = max(DP[all_qfits<i]+...) \]

algorithm1 O(n2 or n): DP[i] means DP max until i \[ DP[i] = max(DP[first_q fits <i]+...) \] Note: the opt come up like this: we only need max from all_qfits<i so basically we only need to keep max to DP[first_qfits], so meet the demands and cut the unless crap.

class Solution {
  public:
      int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
          int sz = startTime.size();
          vector<vector<int>> index(sz, vector<int>(3,0));
          for(int i=0; i<=sz-1; i++) {index[i][0]=endTime[i], index[i][1]=startTime[i], index[i][2]=profit[i];} sort(index.begin(), index.end(), [](vector<int>&a, vector<int>&b){return a[0]<b[0];});
          vector<int> dp(sz+1, 0); int ma = INT_MIN;
          for(int i=1, j=0; i<=sz; i++, j=i-1){
              dp[i] = dp[i-1];
              while(j>=1 && index[j-1][0]>index[i-1][1]) j--;
              dp[i] = max(dp[i], dp[j]+index[i-1][2]);
          }
          return dp[sz];
      }
  };

3.18.21. 1043. Partition Array for Maximum Sum

key:
- $O(nk)$ observation: dp[i] is the largest from 0 -> i-1 & separate i-1|i \[ dp[i] = max(dp[i], (i >= k ? dp[i - k] : 0) + curMax * k); \]

3.18.22. Best Time to Buy and Sell Stock III

key

observation: separate the problem to max(DP_1[i] + DP_2[i+1]) and \[ DP_1[i].second = max(DP_1[i-1].second, A[i]-DP_1[i-1].first) \]

class Solution {
public:
    vector<pair<int,int>> left, right;
    int maxProfit(vector<int>& prices) {
        int sz = prices.size(); if(!sz) return 0;
        left.resize(sz), right.resize(sz); left[0] = {prices[0], 0}; right[sz-1] = {prices[sz-1], 0}; 
        for(int i=1; i<=sz-1; i++){
            left[i] = {min(left[i-1].first, prices[i]),
                       max(left[i-1].second, prices[i]-left[i-1].first)};
        }
        
        for(int i=sz-2; i>=0; i--){
            right[i] = {max(right[i+1].first, prices[i]),
                        max(right[i+1].second, right[i+1].first-prices[i])};
        }
        
        int max_ = INT_MIN; for(int i=0; i<=sz; i++){
            auto l = (i==0)?0:left[i-1].second; auto r = (i==sz)?0:right[i].second;
            max_ = max(max_, l+r);
        }
        return max_;
    }
};

### 689. Maximum Sum of 3 Non-Overlapping Subarrays

key
- observation: \[ dp[i,3] = max(dp[i-1,3] or 0 , dp[i-k,3-1] or 0) \] Note: that the hard part is how to record all 3 indexes. As top-down is too comsuming, bottom up is preferred.

3.18.23. 877. Stone Game

key
- $O(2n^2)$ observation: min_max is double dp problem, dp[l][r][i] means the maximum difference(A-B) of piles can get & minimum difference (A-B) of piles. The reason we use difference instead of value A & B, is because we don't want to carry more information. \[ dp[l,r,1] = max(p[l]+dp[l+1,r,0],p[r]+dp[l,r-1,0])\\ dp[l,r,0] = min(-p[l]+dp[l+1,r,1],-p[r]+dp[l,r-1,1]) \]
- $O(n^2)$ observation: get rid of min process => min max is actually the same thing, we want dp[i][j] to represent the difference of chooser-opponent. \[ dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]) \]

3.18.24. 375. Guess Number Higher or Lower II

key
- $O(n^3)$ observation: this problem is tricky, we want the min count for guarantee a win, which is a min(max(..)) problem, define dp[i][j] for mincount to a win if guess is in [i,j]. we have the following equation. So actually minmax problem the opponent side chooses max/min depending on result of dp(optimal strategy) \[ dp[i][j] = min(dp[i][j], x+1+max(x-1<i?0:dp[i][x-1], x+1>j?0:dp[x+1][j])); \]

3.18.25. 664. Strange Printer

key

$O(n^3)$ observation: set dp[i][j] = minimal operations needed for string[i->j]

optimization: first we use reg to compress the string:

1	s = ''.join(a for a, b in zip(s, '#' + s) if a != b)

then for the propagation function, we have equation below, the idea is that for the s[l], we only print once( we first sort all print by first element appearance, if there's more than 1 print involves s[i], we eliminate all other and left 1, the result remain the same), so we must have print start with s[i] in optimal. So how do we d&c ? We d & c on how long will that print start with s[i] last: problem = {s[i] ensds at i, ends at k where s[k] = s[i]} we don't need to consider all other k where s[k] != s[i] because it is the same as {ends at k2 where s[k2] = s[i] and k2 is the maximum that satisfy this condition and < k}, so here we have the equation below. And also nice that the reason we can split like this, is that if s[i] == s[k] and we have all elements in p[l->k-1] does not exceed k (because i->k is one print) so we can split the problem.

\[ dp[l][r] = min(dp[l][k-1]+dp[k+1][r]) \text{if s[k]==s[l],$k \in[l+2,r]$} \]

for r in range(1, len(s)):
     for l in range(r-1, -1, -1):
       for i in range(l+2, r+1): #[l+2, r]
         if s[i] == s[l]:
     dp[l][r] = min(dp[l][r], dp[l][i - 1] + (dp[i + 1][r] if i + 1 <= r else 0))
       return dp[0][-1]

note: https://leetcode.com/problems/strange-printer/discuss/118769/Proof-of-O(n3)-algorithms, dp[xx] involves printing s[l] all over l->r, so this is additional information, which is why we have to use dp[l->k-1] instead of dp[l+1->k-1], because dp[l+1, k-1] does not imply that all s[l] in that period is pre-panted by dp[l->r], however in dp[l->k-1] we first paint s[l] to l->k-1, from which we can extend k-1 to r(or to k) and have this => dp[l->k-1] = {paint l->k-1 + rest of l->k-1}, dp[l->k-1] + dp[k+1->r] = {paint l->k-1 + rest of l->k-1 + rest of k+1->r} ={paint l->r + rest + rest } = dp[l->r]

3.18.26. 576. Out of Boundary Paths

key:

$4^N$ observation: dfs

$O(nmN)$ observation: \[ dp[m][n][L] = \sum dp[around][L-1] \]

for lay in range(1,N+1):
	for i in range(1, m+1):
		for j in range(1, n+1):
			for x,y in dir:
				dp[i][j][lay] += dp[i+x][j+y][lay-1];

3.18.27. 1298. Maximum Candies You Can Get from Boxes

key

$O(n)$ observation: pos = possible starts, new_t = t round starts. so in t round, start from new_t and add to pos if door is locked and no keys, remove from pos to new_t+1 if meet keys.

if root not in self.k and not status[root]: 
              self.possible.add(root); return 0; # 先碰到的情况
          self.new |= (self.possible & set(keys[root]));
          self.possible -= set(keys[root]);

重点在于维护self.possible的正确性，想象每一轮把能开的都开了，然后停止：所以分为两个步骤先遇到卡门，后遇到钥匙。先加入pos，后把pos一部分转移到new。当new没有增加的时候，也就是凉凉的时候了。

这是一个多步骤dfs，每一步做到不能做为止，然后为下一步选择起点，

这个过程可以想象为KZKKKKKKZZZKKKKZZKZKZKK，k是卡门，z是走，所以我们下一步是k的子集，也就是pos的子集，z的时候取一部分pos即可。

### box remove

key
- $O(n^3)$ observation: let dp[i][j][k] 是以消除i到j的最大值，且i前面有k个和i相同的，且i和前k个一同消除
  
  我们分类的思想来自于，第i个一起消除的后面的第一个和i相同的元素是什么，假设它为m。 \[ dp[i][j][k] = dp[i+1][m-1][0]+dp[m][j][k+1] \quad m \in[i+1,j] T[m] = T[i] \] 所以这个意思就是和第一个碰到的之间的东西，都消掉（k=0意味着这是一个独立的问题和前后无关），k+1意味着消掉后，i和前k个和第m个凑到了一起，且他们会一起消掉这样子。这个更新顺序很烦人，是一个柱子一个柱子这么来的。

3.19. depth first search

排列问题 Permutations。第 46 题，第 47 题。第 60 题，第 526 题，第 996 题。
组合问题 Combination。第 39 题，第 40 题，第 77 题，第 216 题。
排列和组合杂交问题。第 1079 题。
N 皇后终极解法(二进制解法)。第 51 题，第 52 题。
数独问题。第 37 题。
四个方向搜索。第 79 题，第 212 题，第 980 题。
子集合问题。第 78 题，第 90 题。
Trie。第 208 题，第 211 题。
BFS 优化。第 126 题，第 127 题。
DFS 模板。(只是一个例子，不对应任何题)

3.19.1. 282 addopeartion

key:
- observation: is easy => 4^n algorithm, no other way?
  
  => cur[i+?] = cur[i] +-* cur[i:r]; and be careful that when cur[i:r] start with 0 such as 01 => it can't be treated as a number, so we skip it .

3.19.2. 315. Count of Smaller Numbers After Self (from D&C)

key:
- observation: the observation is not intuitive!!!:((((
  
  => cur[i, j] = cur[i, mid] + cur[mid+1, j] + between(left and right）and if we could somehow sort this left & right, the between procedure is O(n)， so, merge sort.
- algorithm2:
  
  => cur[i] = smaller[i+1:end] => insert cur[i] into [i+1:end] and see how many is smaller.(this is usage of BST)
careful
- empty!!
- INT_MIN not -1

3.19.3. 514. Freedom Trail

key:
- observation: separate the problem to [0: i-1] + from[i-1 to i] + [i: size-1]

3.19.4. 401 Binary Watch

key
- observation: we can depth first search => by setting the same level as same number of bits. and add 1 to it until gg.

3.19.5. Different Ways to Add Parentheses

key
- observation: suppose we have a final signal /-/+ (e.g. (3-1) (2-3) *is the final) and we can separate the equation to 2 part => $sum(1, sizeof(n)) =(sum(1, i) */-/+ sum(i+1, sizeof(n))) \text{ for i in [1, sizeof(n) -1]}$. so this becomes easy.

3.19.6. upper lower letters

key
- observation: i th level is the string with ith first elements dealt with.

3.19.7. 93. Restore IP Addresses

key
- observation: ith level is the left dots to put , i = 1,2,3,4, so conditions on i =1 .

3.19.8. 306 additive number

key
- observation: 2 pointer exhaustion, DFS, the hard part is the margin condition
- algorithm2: or you can optimize it by using 3 arrays/bitset to indicate if col/skewedleft/skewed right is full.
careful
- always careful with the margin especially when dealing with arrays!!!

3.19.9. 51. N-Queens

key: track this shit
careful:
- with the bit manipulation

3.19.10. 47. Permutations II

key: ...ez

3.19.11. 89. Gray Code

key: ...ez
careful:
- conditions when we find and cut all other loops.

3.19.12. 131. Palindrome Partitioning

key: the same level means the number of dots in between

3.19.13. 17. Letter Combinations of a Phone Number

key; the same level means the number dealt with
careful
- empty input

3.19.14. 126. Word Ladder II

key; same level means the number of findings
careful
- auto a = vector do not necessaily copy ???
- reserve carefully or always puck back

3.19.15. 44. Wildcard Matching

key:

observation: if the previous (say i-1 th ) is set, and we meet the ith , then if * doesn't meet demands, then we don't need to go back to i-1. this can be proved by constract. so we use a greedy DFS(add trimming) to solve this.

algorithm2: the above algorithm can be implemented in iteration, we have the following 5 conditions:

if s==p or p =='?', we move +1
if p=='*', we record/update the position now for future usage
if s!=p

(3.1) if we met * before, go back

(3.2) if we haven't, return false.

if p is empty, return true.
if s is empty (out of while),

(5.1) if p consist only of "*", return true.

(5.2) if not, return false.

bool isMatch(string s, string p) {
  auto sp = s.begin(), pp = p.begin(), spp = s.end()+1, ppp = p.end();
  while (sp != s.end()){
    cout<<s.substr(sp-s.begin()) <<" "<<p.substr(pp-p.begin())<<endl;
    if (*sp==*pp || *pp=='?') {sp++; pp++;}
    else if (*pp == '*') {spp = sp+1; ppp = ++pp;}
    else if (spp != s.end()+1) {sp = spp++; pp = ppp;}
    else return false;
  }
  while (*pp == '*') pp++;
  if (pp == p.end()) return true; else return false;
}

3.19.16. 37. Sudoku Solver

key
- $O(9^n)$ observation: key point of solver is always build the map for searching. We first sort out all [i][j] undetermined elements into an array, level ith means [0,i] number is dealt with. and each node we have 9 options for searching.
careful
- return when possible(trimming)
- careful with the return conditions

3.19.17. Stickers to Spell Word

key
- observation: is easy, level ith = adding i stickers, use vector<26 ,int > to indicate a word
- algorithm2: improve, the result is like this:[sticker f, c, g, c, d], we want to trim this dfs.
  
  First observation is that it contains duplicate so that we save the fucker. Second observation is that dfs contains unnecessary search branchs where no targets are covered. Third observation is that this dfs do not concern with sequential since it's a set, so we want to trim this fucker by sorting so that it do not contain duplicate, however this is not feasible (such as b, f, g, g or g, b, f, g, they are on different path) SO, we can do by using an alternative method: sorting. but how can we do that? we can sort them on something we already know when we reach the node, in this case, it will be the sequence on covering the target string, note that this does not necessarily trim all duplicate sequences. (if a, b, c / c, a, b all contains target[0], target[1], target[2], then it's a duplicate). so this is a partial soring.
- algorithm3: use full sorting => can't use DP since it's not fully searched.

3.19.18. 996. Number of Squareful Arrays

key
- observation: DFS
- algorithm2: avoid duplicate, on each level => derive that no same sequence is made

3.19.19. 1240. Tiling a Rectangle with the Fewest Squares

key
- observation: use array of height to represent a rectangle, and do DFS
- algorithm2: set DFS have duplicates, search from largest => smallest, (note that we may hve irregular DFS, so the hard part is to determine search sequence). so actually we want the best searching sequence that both contains optimals and eliminate duplicate as much as possible. so we focus on the leftest highest 1x1 square and we can do 1x1,2x2.....min(height,width)x2, this is both full search as well as min branches.

3.19.20. 980. Unique Paths III

key is easy DFS+DP
careful
- with count considering -1
- with DP saving and index restoring

3.19.21. 888. Decoded String at Index

key
- actually a one-way dfs with mod and divide, a math problem basically.
carefull:
- with mod
- with //

3.19.22. 778. Swim in Rising Water

key
- observation: no duplicated path: imagine like fill in all blanks only once. set global trimming. 想象一个树杈，然后每个搜索不会有重复的树杈交叉在一起。之所以可以这么做是因为搜索前面的信息不会影响后面，所以一旦后面搜不到了那就是凉了；其他会交叉的题比如8皇后（前面皇后的位置会影响后面的搜索是否成功），比如找钥匙（前面走的路决定了有多少吧钥匙所以会影响后面）。

3.19.23. 1255. Maximum Score Words Formed by Letters

key
- observationO(2^n): dfs
- max pruning: branch and bound, prun those curr_score + sum(words_score[i:]) <= self.max_score
careful
- use vector<26> to store set<>

3.19.24.

key: make sure the conditions:

Note: that some times conditions are hard to implement in tree because the level structure, use parameters to add additional information.

return value => node child info: node update

para value => node parent info: leaf update/ trimming

class Solution {
public:

    int dfs(TreeNode* root, bool have_node, bool monitored){
        if(!root) return 0;
        if(have_node){
            auto temp_left = dfs(root->left, 0, 1), temp_right = dfs(root->left, 0, 1);
            return temp_left+temp_right+1;
        }
        if(monitored){
            auto take_none = dfs(root->left, 0, 0) + dfs(root->right, 0, 0);
            auto take_top = 1 + dfs(root->left, 0, 1) + dfs(root->right, 0, 1);
            return min(take_none, take_top);
        }
        if(root->val) return root->val;
        auto take_left = dfs(root->left, 1, 0) + dfs(root->right, 0, 0);
        auto take_right = dfs(root->left, 0, 0) + dfs(root->right, 1, 0);
        auto take_top = dfs(root->left, 0, 1) + dfs(root->right, 0, 1)+1;
        return root->val = min(min(take_left, take_right), take_top);
    }
    int minCameraCover(TreeNode* root) {
        return dfs(root, 0, 0);
    }
};

3.19.25. 689. Maximum Sum of 3 Non-Overlapping Subarrays

key
- observation: \[ dp[i,s] = max(dp[i-1,s+k+\epsilon]) \]
observation: using top-down implementation. \[ dp[i,s] = max(dp[i,s+1], dp[i-1,s+k]) \]
careful
- careful with the return conditions

3.19.26. 761. Special Binary String

key
- observation: imagine like parenthesis =>Like if we put another "()(())" inside "()(())", like "()(( ()(()) ))".
  
  we can prove that S = ( S* ) . dfs(i) returns max sub special start with i and end with the first special satisfaction. for example => () + ( () () ) => dfs(0) + [dfs(3) + dfs(4)]
  1
  dfs = (+dfs(i+1)+)

### 913. Cat and Mouse

key
- observation: DFS adversarial search problem,dfs[x][y] means if optimal solution will win for cat/mouse. the only part is how to determine draw for dfs[x][y].
  
  It is difficult to prove that all catch/reach will succeed in 2n steps.

3.19.27. 488. Zuma Game

key

ez greedy observation: try to at least eliminate some balls at each round, then do dfs.

int findMinStep(string board, string hand) {
    if(board.size() == 0) return 0;
    int res = hand.size()+1;
    for(int i = 0; i < board.size(); ) {
        int cur_steps = 0, cnt = 0;
        char ball = board[i];
        // try eliminate current ball
        while(i < board.size() && board[i] == ball) {
            i++;
            cnt++;
        }
        // insert 3-cnt balls, remove it from hand
        if(count(hand.begin(), hand.end(), ball) >= 3-cnt){
            cur_steps += 3-cnt;
            string newhand = hand;
            string left = board.substr(0, i-cnt);
            string right = board.substr(i);
            string newboard = generate(left, right);
            // remove used balls
            for(int k = 0; k < 3-cnt; k++) {
                newhand.erase(newhand.find(ball), 1);
            }
            int furtherSteps = findMinStep(newboard, newhand);
            if(furtherSteps != -1) {        
                res = min(res, cur_steps+furtherSteps);
            }                
        }
    }
    return res == hand.size()+1 ? -1 : res;
}
// generate new board from left and right
string generate(string left, string right) {
    int j = left.size()-1, k = 0, dup = 0;
    while(j >= 0 && left[j] == right.front()) { j--; dup++; }
    while(k < right.size() && right[k] == left.back()) { k++;dup++; }
    if(dup >= 3) return generate(left.substr(0, j+1), right.substr(k));
    else return left+right;
}

note: however this greedy is wrong due to a test case like "RRWWRRBBR[w]R", "WB", where you don't have to eliminate anything at first round.

3.19.28. 473. Matchsticks to Square

key

observation: dfs is trivial
optimization1: put large matches in the front so if it outranges lengths we can eliminate this solution

$2^N*4N$ optimization2: our solution = dfs(already, mask-1) || dfs(already, mask-2) || dfs(already, mask-3)，

each dfs refers to whether can succeed using mask matches & already has been built and only 1 side is being build(我们总是在一个没完工墙上搭火柴所以不会出现两个没完工墙的情况)，duplicated case in this scenario is when (already, mask) appears more than once which imply that we have same set of matches and same current wall which simply means same result.

class Solution:
    def makesquare(self, nums: List[int]) -> bool:
        su = sum(nums);
        if su%4: return False;
        le = su/4;
        # c = collections.Counter(nums); 
        nums = sorted(nums);
        mask = (1<<len(nums))-1;
        save = {}
        def dfs(already=0, mask=mask):
            if already == 4:
                return True;
            used = 0;
            for g in range(len(nums)):
                if not ((1<<g) & mask): used += nums[g];
            currentleft = le - (used - (already)*le);
            if (currentleft, mask) in save: 
                return save[(currentleft, mask)];
            
            for g in range(len(nums)):
                if (1<<g) & mask:
                    if nums[g]<currentleft:
                        mask ^= 1<<g;
                        if dfs(already, mask):
                            save[(currentleft, mask)] = True;
                            return True;
                        mask ^= 1<<g;
                    if nums[g]==currentleft:
                        mask ^= 1<<g;
                        if dfs(already+1, mask):
                            save[(currentleft, mask)] = True;
                            return True;
                        mask ^= 1<<g;
            save[(currentleft, mask)] = False;
            return False;
        return dfs();

3.20. breadth first search

3.20.1. 401 Binary Watch

key
- observation: we can breadth first search => by setting the same level as same number of bits.

3.20.2. 126. Word Ladder II

key:
- observation is very important in this problem. as you can see why we prefer BFS over DFS.That first we only want the shortest=> that's natural advantage, since it means that depth is fixed and all possible answers appears on the same level that we don't necessarily need to exhaust the tree(DFS on the other hand do not have this advantage). Secondly, on the same level, we can see that we can separate the problem into this: the next steps on next level do not appear on the above levels(why? because you can prove that if it exists on the above level, it is not the shortest anymore), so this feature means we can expedite the BFS search by narrowing down possible next steps.

3.20.3. 691. Stickers to Spell Word

key
- BFS is obvious but not necessary, but keep in mind that string matching you can always use int.
careful
- vector<vector{size, vector()}
- don't use auto when vector<vector
- don't copy the whole string/ avoid using vector, use 2^n-1.

3.20.4. 864. Shortest Path to Get All Keys

key
- BFS through that trimming when no keys are acquired.
careful
- C++ map is lousy
- bitset.tolong()

3.20.5. 1125. Smallest Sufficient Team

key
- observation: bfs
- trimming: since it's bfs, trim those with same level branches.
careful
- for loop check states!
- 1<<i (check for LL!)

3.20.6. 662. Maximum Width of Binary

careful
- with the poping operations
- with int64 overflow

3.20.7. 854. K-Similar Strings

key
- observation: that at most n swaps will do. each swap -1/-2
  
  Note: at each layer fix the first element. this ensures a optimal solution. basically, the swapping tech is to find the maximum island numbers, at each level we open n new branches which is new ways of spliting components. The swapping of fixing the first or not fixing the first is the exact same but opposite sequence.
  
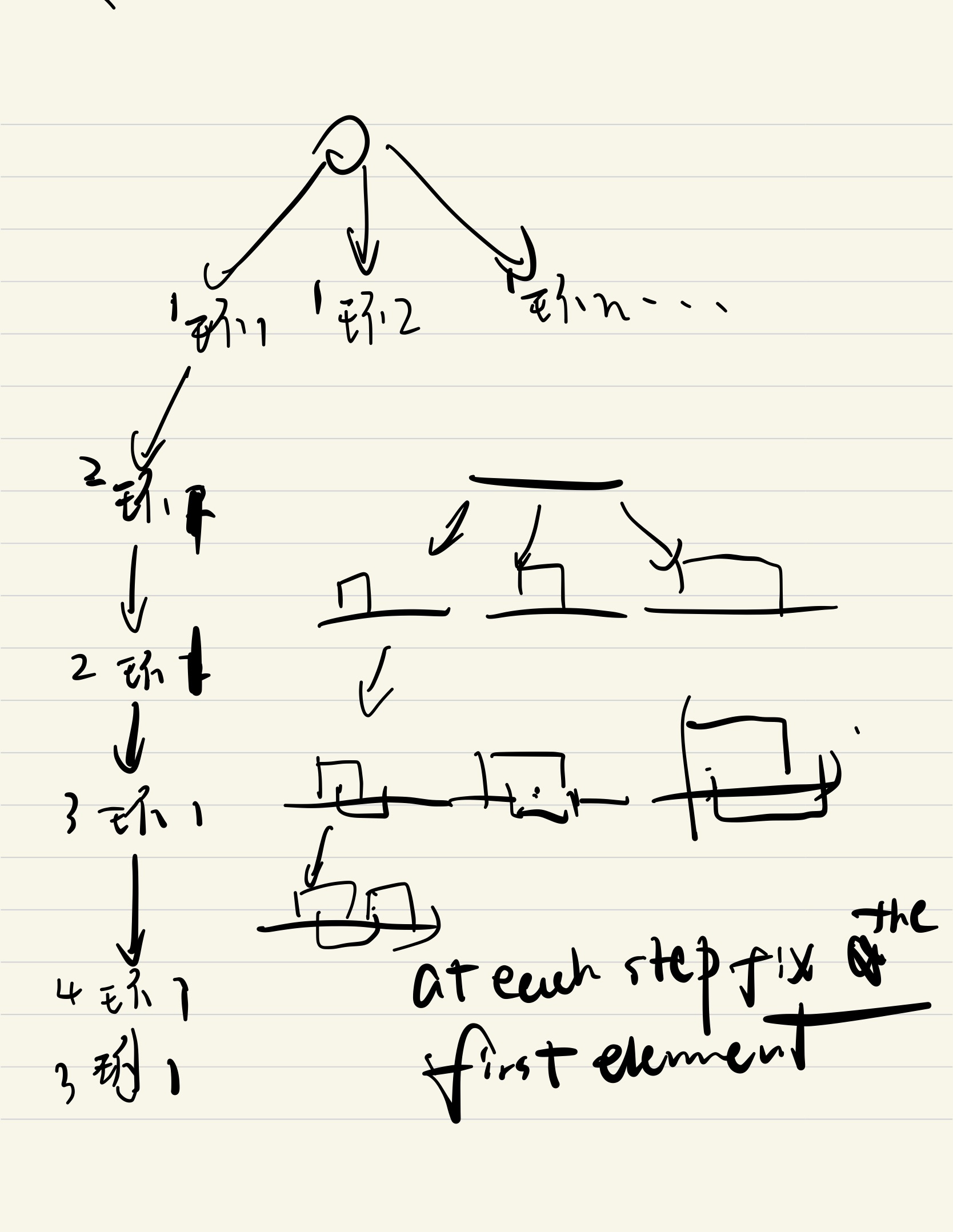
  Untitled-4
- optimization: since our goal is to maximize the components, then if we can swap for -2, we stop there. This is optimal because

3.20.8. 1162. As Far from Land as Possible

key
- $O(kn^2)$ observation: intuition is go from any point of 0, but it is just way too slow
- $O(n^2)$ optimization: go from 1s =>

3.20.9. 675. Cut Off Trees for Golf Event

key
- $O(n^4)$ observation: where we split the problem into {find0->1, find1->2...} and subproblems does not overlap. So shortest path from 0->1 we can use bfs to solve, which is O(n^2),
note:
- don't forget visited = 1;
- here we have edge = 1 so bfs == dijskstra

3.20.10. 1345. Jump Game IV

key

$O(n)$ observation: obvious bfs
optimization: to prevent certain case, we use greedy to push first the farest node.
1
for(int i=ma[arr[cur]].size()-1; i>=0; i--){

optimization: always do return judgement beforehand(在push之前)

for(int i=ma[arr[cur]].size()-1; i>=0; i--){
  auto nex = ma[arr[cur]][i];
  if(nex==cur || visited[nex]) continue;
  if(nex==arr.size()-1) return d+1;
  else {q.push(nex);}
}

3.20.11. 1036. Escape a Large Maze

key
- $O(B^2)$ observation: bfs/dfs with no overlapping & set upper_bound for area = 200*200/2.
- remember: that we always need to do from the end.

3.20.12. 1263. Minimum Moves to Move a Box to Their Target Location

key
- 2-phase bfs observation: bfs on box => move the box to dst, bfs on person=> for each movement of box, we have one and only place for person, so check out with bfs if that person can move to that place.
- opt: use memo, if person and box result appears again => it is duplicated, if only the box same position appears on different level, could it be trimmed? no, becasue maybe the first box has the wrong person position.

3.20.13. 787. Cheapest Flights Within K Stops

key
- observation: bfs with trimming，k step bfs is obvious ，and trim those > upper_bound
dij observation: dij is a type of search that chooses a node to expand by it's value. And although it yields the best result, still log(n) with heap operations, so dij vs BFS we don't know for sure.

3.20.14. 847. Shortest Path Visiting All Nodes

key
note:
- hashmap uses a LOT more mem than set.

3.20.15. 301. Remove Invalid Parentheses

key
- BFS obvious
- op1: avoid consecutive ((
- op2: avoid duplicate sequence(e.g. ()() remove 0/1 = remove 1/0) So we use start variable to make sure all remove elements is in a sequence =>(1,2,3; 2,3; 3...)
- op3: avoid invalid sequence, 比如从start=k开始；那么如果k之前的东西有“（”少于“）”就完蛋了，因为之后补不回来了。所以判断0～k-1是否count>=0

### 1293. Shortest Path in a Grid with Obstacles Elimination

key
- $O(mnk)$: 这个题需要明白什么时候要去重，一般来说visited=set，去过就不再去。但是这个题里，visited=比当前小的k+比当前大的k。我们不能全部去掉，只能去掉比当前大的k，因为有可能尽管步数多于当前但是小k会给未来更多机会所以不能去掉。
- op1: 提前return，由于grid从一个点到另一个点的最短距离是直下直右，所以可以根据k的多少提前判断。并且这个优化也包含了在m-1，n-1的正确解，所以是正确的。

3.20.16. 815. Bus Routes

key
- $O(R*Rlen+R*Rlen)$ 从起始点出发，探索能到达该点的所有点=>
- $O(R+2R*Rlen+Rlen*Rlen*R)$ 如果要从起始线路出发，遍历线路的话，虽然遍历步骤是R，但是要使用intersect操作构建图，该操作的最坏复杂度很糟糕（ O(len(s) * len(t))）。之所以这个是对的，是因为考虑到一次线路不会重复走两遍（否则第一次直接走到第二次的目的地即可），所以一次线路只会经过一次，线路到线路之间的边其实就是起始线路中走一段走到下一个线路。

3.21. BFS+DFS

3.21.1. 1368. Minimum Cost to Make at Least One Valid Path in a Grid

key
- $O(NM)$ observation: think of each element as node and whole grid as a graph, so the
  
  graph is splited into supernodes{SP1, .... SPn} and we start from SP1 want to reach to SPn. So we want min step so BFS is obvious and note that we do BFS on SuperNode not node because only supernode have distance(cost) =1.And dfs help with finding SP by starting with a small node. 这个Supernode的概念是很关键的，比如单纯做dfs会考虑到重复路径，经过重复小节点视为剪掉；实际上经过重复supernode都可以视为剪掉，因为相当于supernode的层面上出现了环，所以cost>=0。观察到联通子集可当作一个super节点是求解本题的关键。

3.22. binary search

3.22.1. 29 divide 2 numbers

key
- observation: the array that numbers m, n can be expressed in binary. and divide can be expressed in binary as well. and we can tell that it is unique. so we try to get the unique result, we can do this by shifting the divider. $2^m*d+2^{m-1}*d+2 ^{m-3}*d$, and m-3 < m-1 < m， so every coefficient is only 1 and smaller each so we can do shifting trick. The original thought is to get every m individually, and this is the original thought to get m involves binary. so this it actually a 31 binary problem => 31 O(n) $ $ O(n)

3.22.2. 1201 Ugly Number

key
- observation: that we can easily compute $f(n)=_{i=1}^{n}I(i ) $, this is how we get the solution: that from max to 1, we find f(k) = n.
careful:
- gcd(a, c, d) = gcd(a, gcd(c, d)) for gcd(a, c, d) $\in$ gcd(c,d)
- lcm(a, c, d) = lcm(a, lcm(c, d))

3.22.3. 50 power(x, n)

key:
- observation is easy
careful
- abs(int) could be dangerous, the following code is more appropriate.
  1
  abs((int64_t)n);

3.22.4. 81. Search in Rotated Sorted Array II

key
- observation is easy
- detail: margin, especially when l > r

3.22.5. 862 shortest subarray with sum at least k

key
- observation: dp that it is similar to max sub problem, this problem is more complicated since we need to search more from max(i-1)'s starting point to i ( in the previous problem, we do not need this step), during the search we can use bs. I thought about how to decrease the searching points during this linear o(n) search, obviously we don't need to search those i with sum(i to j) <0. but here we need N2 storage for the sum(i, j), we could have turn this to linear storage by finding the basis of these sum(i, j) -> sum(i). we only need o(n) to store these element and the algorithm turn to the alternative .
- alternative algorithm: the second algorithm, we can keep more of the array ( in previous problem it is only 1 element min(sum(j)) j <i ), this time we want more elements, the key of the elements is that we want them increasing, to make this happen we do the following: if we find out that in i's time we have sum(i) < array(j) we pop the array until sum(i) is in the array and array is increasing. improvement here: we can discard sum(i) after it's usage since we know that no matter what, substring starts with i will only grow larger.

3.22.6. 1044. Longest Duplicate Substring

key
- observe; we separate this to n subproblems ( find dup substring length = i) and we always know that if longest length = g, then i<=g => I(find sub) = 1 and i > g I (find sub) = -1 . so we use binary search to connect n subproblems. for each subproblem we use rolling hash table to get themO(n) * O(logN) = O(N^2)

3.22.7. 4. Median of Two Sorted Arrays

key:

observation: median = find i and j to separate the 2 arrays. so we don't have subproblems in this problem, instead it is a rather easy searching => we can even find a mono array to accelerate the searching. it is actually a 2 way BS, something like(0001, 1110) you can do 2 way to shorten the paragraph since there are less constraint on the mid variable, but doing my way as a 1 way BS is more explicit but more complicated.

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int n = nums1.size(), m = nums2.size();
    int i = (m+n)%2==0 ? max((n-m)/2-1, -1) : max((n-m-1)/2, -1), r = !(m+n)%2 ? min((m+n)/2-1,n-1): min((m+n-1)/2, n-1);
    int mid = (i+r)/2, mid_2 = (n+m)%2==0 ? (m+n)/2-mid : (m+n+1)/2-mid, j;
    if ( n == 0 ) return m%2==0 ? (nums2[m/2-1] +nums2[m/2])/2.0 : nums2[m/2];
    if ( m == 0 ) return n%2==0 ? (nums1[n/2-1] +nums1[n/2])/2.0 : nums1[n/2];
    while( i < r ){
        mid = ceil((i+r)/2.0);
        mid_2 = (n+m)%2==0 ? (m+n)/2-mid-2 : (m+n+1)/2-mid-2;
        int midr = mid == n-1 ? INT_MAX : nums1[mid+1];
        int mid2r = mid_2 == m-1 ? INT_MAX : nums2[mid_2+1];
        if (midl >= mid2r) r = mid-1;
        else i = mid ;
    }
    j = (n+m)%2==0 ? (m+n)/2-i-2 : (m+n+1)/2-i-2;
    int midl = i == -1 ? INT_MIN : nums1[i];
    int midr = i == n-1 ? INT_MAX : nums1[i+1];
    int mid2l = j == -1 ? INT_MIN : nums2[j];
    int mid2r = j == m-1 ? INT_MAX : nums2[j+1];
    return (n+m)%2==0 ? (max(midl, mid2l) + min(midr, mid2r))/2.0
                      : max(midl, mid2l);
}

carefull:
- i+r/2 or ceil(i+r/2.0)
- no max function with size_t

3.22.8. 719. Find K-th Smallest Pair Distance

key
- O(nlog(max-min) + nlog(n)) observation: a christmas tree can be shown here, we want a line=res so that nodes under res = k, at the same time the larger res is, nodes_under_k is larger. so we want this to solve the problem.
  
  Note: it is O(max-min) to search the nodes under line = res.
  
  IMG_2222

### 786. K-th Smallest Prime Fraction

key
- same as 719
careful
- BS update count & stuff
- count after j and margin conditions

3.22.9. Online Majority Element In Subarray

key

$O(lenofquery)=O(n)$ observation

$O(m*log(len ofsame))$ observation: since we can store occurances and form an increasing array, we can search through the array and use binary search.

class MajorityChecker {
public:
    unordered_map<int, vector<int>> idx;
    MajorityChecker(vector<int>& arr) {
      for (auto i = 0; i < arr.size(); ++i) idx[arr[i]].push_back(i);
    }
    int query(int left, int right, int threshold) {
      for (auto &i : idx) {
        if (i.second.size() < threshold) continue;
        auto it1 = lower_bound(begin(i.second), end(i.second), left);
        auto it2 = upper_bound(begin(i.second), end(i.second), right);
        if (it2 - it1 >= threshold) return i.first;
      }
      return -1;
    }
};class Solution {
public:
vector<int> fallingSquares(vector<pair<int, int>>& p) {
        map<pair<int,int>, int> mp;
        mp[{0,1000000000}] = 0;
        vector<int> ans;
        int mx = 0;
        for (auto &v:p) {
            vector<vector<int>> toAdd;
            cout << endl;
            int len = v.second, a = v.first, b =v.first + v.second, h = 0;
            auto it = mp.upper_bound({a,a});
            if (it != mp.begin() && (--it)->first.second <= a) ++it;
            while (it != mp.end() && it->first.first <b) {
                if (a > it->first.first) toAdd.push_back({it->first.first,a,it->second});
                if (b < it->first.second) toAdd.push_back({b,it->first.second,it->second});
                h = max(h, it->second);
                it = mp.erase(it);
            }
            mp[{a,b}] = h + len;
            for (auto &t:toAdd) mp[{t[0],t[1]}] = t[2];
            mx = max(mx, h + len);
            ans.push_back(mx);
        }
        
        return ans;
    }
};

3.22.10. 699. Falling Squares

key
- $O(n^2 )$ observation: save in map, use binary search and update
- $O(nlogn)$ observation: Similar to skyline concept, going from left to right the path is decomposed to consecutive segments, and each segment has a height. Each time we drop a new square, then update the level map by erasing & creating some new segments with possibly new height. There are at most 2n segments that are created / removed throughout the process, and the time complexity for each add/remove operation is O(log(n)).
- $O(n^2)$ observation: using a Binary Search Tree, not necessarily a Segment Tree, just do the same job as the first map & binary search solution. I don't get it why this is so much faster than mapping.
- $O(n logn)$ observation: use a Segment Tree, obviously we need to do range_sum & range_query.

3.22.11. 850. Rectangle Area II

key
- $O(nm) $ observation: do all the settings square by square.
- $O(n^2)$ observation: discretion, do all the settings split by split.
- $O(nlogn) $ observation: discretion + vanilla segment tree(since we have range_update $O(logn) $ )
careful:

d

3.23. greedy search

3.23.1. wildcard matching

key
- observation(unique trimming) trim all branches of * which is not the last bit.
  
  imagine that take * => 0 as local greedy then until meet next *, local greedy is global greedy.

3.23.2. 402. Remove K Digits

key
- observation:(unique trimming) set the 1st element => 1+1st element => 1+2...
  
  Proof: (1) DP[1] is setting 1st as smallest
  
  (2) DP[2] is setting 2nd as smallest and can be derived from DP[1]

3.23.3. Remove Duplicate Letters

key
- observation:(unique trimming) basically same as Remove K Digits , adding constraints on poping operation, goal is to set the first bit as soon as possible.
  
  Proof: actually a pretty trivial proof, that at ith level we set the smallest possible outcome for [1:i], since the poped element can replenished after ith step and we'll always get smaller outcome by poping those items. So it is a greedy local optimal solution which yields global optimal.


#include<iostream> using namespace std; int main() 
{  int x=0, i = 0, j = 1;//i执行次数 j=1最后猴子拿到的桃子数， x 每次均分后，第一只猴子拿了之后剩下的总数  
 while (i < 5) { 
   x = 4 * j; 
   for (i = 0; i < 5; i++) 
   {  if (x % 4 != 0) //检查看到的桃子是否是4的倍数  
   {   break;  } 
    x = (x / 4) * 5 + 1; 
   1 
   1*4 5 + 1 = 6
   6*4 30 + 1 = 31
   } 
   5x + 1 => 4x =s 5y+1 => 4y = 5z+1 => 4z
   j++;  }  
 cout << x << endl;  return 0; }

3.23.4. 871. Minimum Number of Refueling Stops

key
- observation:(directly solving subproblem) go further in t stops and you local optimal = global optimal
  
  IMG_3698

3.23.5. 502. IPO

key
- greedy, go for the largest possible => heap . same as 871

3.23.6. 330. Patching Array

key
- observation: 从[1：最小的set里的数]这个区间出发，1）不断找当前不能表示的最小数是什么 2）如果能cover掉一些白送的数，不断加上白送的数，维持一个能表示的最大区间。思维固化，只想到1248，但其实1245也是能包括0到12的数的。
  
  Proof: (0) we change the min problem to max => DP[i] is the largest number to cover by adding i elements.
  
  (1) smallest problem DP[1] is the largest cover by adding 1
  
  (2) the next DP[i+1] can be solved by adding the number DP[i] can't solve. proof is easy.

3.23.7. 630. Course Schedule III

key
- observation: we prove DP[i] means optimal from [0:i]
  
  $DP[q][j] = min_{i \leq q}(DP[i][j-1] + course[i] )$ => so to get min(DP[i][j-1]) is equivalent to pop the largest.
  
  Proof: 用数学归纳法证明：如果是更新+1，那么就是直接加新来的；如果是平行+0，那么要么是加了最新的然后原来的j-1，要么不加最新的。这个取决于最新的和原来最大值的大小。简而言之，greedy直接把min(DP[i][j-1])这一项给解出来了，而不需要大费周折去更新他。这个简化的关键是发现DP[j-1]和DP[j]其实差的那一个element是j中的最大值，有了这一个观察就可以直接求element中的最大值从而直接比较DP[j-1]和DP[j]了，而不需要具体的DP[j-1]的值，也就不需要DP了。
  
  IMG_5430
  
  Proof: if DP[i] is have i

3.23.8. 321. Create Maximum Number

careful:
- vector > vector => 逐个比较。而不是比较整体int的大小
- 临时变量不是左值不能放在引用参数上。

3.23.9. 1353. Maximum Number of Events That Can Be Attended

key
- $O(n logn)$ observation: at each point, we choose the time event with shortest end time. For at each time point, all queue = {all events you can choose at this point}, and by choosing the smallest, you always get the best result.

3.24. sorting

深刻的理解多路快排。第 75 题。
链表的排序，插入排序(第 147 题)和归并排序(第 148 题)
桶排序和基数排序。第 164 题。
"摆动排序"。第 324 题。
两两不相邻的排序。第 767 题，第 1054 题。
"饼子排序"。第 969 题。

3.24.1. 164. Maximum Gap

key

observation: bucket sort => since we only need the interval between 2 buckets, and max interval >= (max-min)/n-1 which is average interval, so bucket size have to be (max-min)/n-1 [) or smaller so that we satisfy size < interval. and basically that's the key point. so that every possible max pair lies in adajacant buckets.

Note: bucket sort's first step is a partial sorting where you fill number into gaps, and we only need gaps in this problem.

class Solution {
public:
   int maximumGap(vector<int>& nums) {
        const int n = nums.size();
        if(n<=1) return 0;
        int maxE = *max_element(nums.begin(),nums.end());
        int minE = *min_element(nums.begin(),nums.end());
        double len = double(maxE-minE)/double(n-1);
        if(!len) return 0;
        vector<int> maxA(n,INT_MIN);
        vector<int> minA(n,INT_MAX);
        for(int i=0; i<n; i++) {
            int index = (nums[i]-minE)/len;
            maxA[index] = max(maxA[index],nums[i]);
            minA[index] = min(minA[index],nums[i]);
        }
        int gap = 0, prev = maxA[0];
        for(int i=1; i<n; i++) {
            if(minA[i]==INT_MAX) continue;
            gap = max(gap,minA[i]-prev);
            prev = maxA[i];
        }
        return gap;
    }
};

3.24.2. 41. First Missing Positive

key
- $O(nlog(n))$ observation: sort & iterate
- $O(n) $ observation: partial soring technique: first we know possible answer = 1->sizeofarray, so if 1 -> sizeofarray is on where they are, then we can go in one turn. so go for swaping 1->sizeofarray to where they should be .
  
  Note: this stem from the fact we can sort 1->n in O(n).

3.25. math

3.25.1. 1352. Product of the Last K Numbers

key
- $O(n)$ observation: use map to store all k
- $O(1)$ observation: use prefix array

3.25.2. 907. Sum of Subarray Minimums

key
- observation: 这个问题本来的局势是把所有幂集的最小值加起来，我们先对最小值做一个聚集，然后通过问题本身的性质进行解决。

3.25.3. 456. 132 Pattern

key
- observation: (unique trimming) the 132 pattern, as we can see we'll expedite the progress if we go from right to left and search for 32 pattern(why? since we can use greedy to keep the largest (3,2) pairs so far), the greedy can be proved that the greedy method is optimal as we move to[i+1,end]. prove by contrast, if point i have 132 pattern but not with greedy, then either 3/2 is not largest. In other words, keeping 32 pattern to be the largest possible will always yield best results.
  
  Proof: (0) can be proved that problem reduce to several partial largest (3,2) pairs, would't call it greedy though
  
  IMG_3650

3.25.4. 765. Couples Holding Hands

key
- observation: when one needs to keep i == function[i] of an array => use circle swapping.
  
  such as i == row[i] where you sort an (0:i) array, or ptn(pos(ptn(row[i]))) which means the correct position row[i] should be, e.g. row[i] = 5, then it should be whereever next to 6(only one position), so by circling swapping, eventually i = 0 gets its correct element then we move to i = 1 and more. There are m distinct no overlap circling rounds and can be proved optimality.
  
  Note: why circles ? because every swap fix 1 pixel, and doing in circle do not affect other elements beside the circle. 如果有一个圈的话，每一次修好一个元素，一个圈的元素数又是固定的，且对圈外无影响，所以必定会修好且最优。图像化来想的话，一个圈的就是m个cuples，每对cuples之间在i,i+1有从两对cuples中各出一个元素。

3.25.5. 995. Minimum Number of K Consecutive Bit Flips

key
- greedy: always fix the current node. Before and after any flip, any bit in the sequence of 1 starting from the left-most bit should not be flipped anymore.
  
  Proof: The greedy claim gives a solution S. Without loss of generosity, let the i-th bit be the first 0 bit. Suppose the greedy claim above is false, then there must be a better (better means less flips) solution S' in which bits in range [J , J + K - 1] are flipped and J < i. There could be multiple J. Let j be the smallest possible J. Since A[j] now is 1 (why? because j), if we flip it,A[j]becomes 0.A[j]finally should be 1, soS'must flipsA[j]again sometime later. Asjis the smallest ofJ,S'can't flip anything left toA[j], which means only flipping the range[j , j + K - 1]can flipA[j]back to 1. See? we flipped[j , j + K - 1], then again[j , j + K - 1].S'wasts flips. IfS'exists, we can find a third solutionS''that is strictly even better thanS'. And we can do this induction infinitely and find a solution needs only 0 or even negative number of flips. -- That is of course impossible. Actually, the induction of finding even better solutions will eventually give youS.Sis strictly better thanS`? Of course not! -- So the greedy claim above is NOT false. So, the greedy claim is true.
  
  Proof2: 首先确定每一个点最多flip一次，然后对每个点排序，找到最左的点，它的左边一定全是1，然后这个点到第二个点中间一定全是1。就证完了其实不是greedy，因为只有一个解。

3.25.6. 927. Three Equal Parts

key

observation: easy problem

class Solution {
public:
    vector<int> threeEqualParts(vector<int>& A) {
        int sz = A.size(); vector<int>index; for(int i=0; i<=sz-1; i++) if(A[i]==1) index.push_back(i);
        if(index.empty()) return {0, sz-1};
        if(index.size()%3) return {-1, -1};
        int m = sz -1 - index.back(); int start = index[index.size()/3-1], start_n = index[index.size()/3], end = index[index.size()/3*2-1], end_n = index[index.size()/3*2];
        if(start_n-start-1 >= m && end_n-end-1 >= m){
            int cur_s = start, cur_n = end, cur_f = index.back();
            while(cur_s!=index[0] && cur_n!=start_n && cur_f!=end_n){
                if(A[cur_s]!=A[cur_n] || A[cur_n]!=A[cur_f]) {break;}
                cur_s--, cur_n--, cur_f--;
            }
            if(cur_s==index[0] && cur_n==start_n && cur_f==end_n) return {start+m, end+m+1};
        }
            
        return {-1, -1};
    }
};

3.25.7. 135. Candy

key
- observation: left recursion will set all + left to m, right recursion set m and + right to m.
  
  IMG_9352

3.25.8. 710. Random Pick with Blacklist

key
- observation: math sampling problem => how to sample from set(N - blacklist) ? since we want prob = 1/len(set(N-blacklist)) = 1/(N-B), so we choose from 0->N-B to make sure whitelist prob is correct then we remap the blacklist to whitelist that>N-B, the reason we do so is because randint can only choose from continuous numbers.

3.25.9. Sum of Subsequence Widths

key
- observation: sort first then, set each pixel as first / second
  1
  count += -A[i] * (1<<i -1) + A[i] * (1<<n-i-1 - 1)
- optimization: to avoid overflow use * constant & + constant, we compute count in iterative manner :
  1
  count = (A[i]%int(1e9+7)+(count*2)%int(1e9+7))%int(1e9+7);

### 1074. Number of Submatrices That Sum to Target

key
- $O(n^3)$ observation: first choose 2 rows, reduce the problem to find subarray if we know the sum of all rows in between, so we sum prefix of matrix. basically this is $O(n^2)$ row choosing * $O(n)$ find target.

3.25.10. 363. Max Sum of Rectangle No Larger Than K

key
- $O(n^3 logn)$ observation: same idea as above, use insert & sort technique.

3.25.11. Transform to Chessboard

key
- $O(n)$ observation: this is a easy problem actually, see if sz is odd/even and it's done.

3.25.12. 843. Guess the Word

key
- observation: basic idea is test a word & eliminate, so the choice of words is important, we want to choose a more common word, which means each letter on position 1->6 are more common. So that if it fails (guess=5/6, we can eliminate more)

3.25.13. 398. Random Pick Index(Reservoir Sampling)

key
- observation:

3.25.14. on line

note: compare have to be static?

3.25.15. 963. Minimum Area Rectangle II

key
- $O(n^3)$ observation: do loop x 3 and map. Note that for rectangle , the sequence of accessing it is irrelevant , (all rectangles are accessed 3 times) so we can assume a way.

### 519. Random Flip Matrix

key
- observation: swapping algorithm=> swap when

3.26. brutal

3.26.1. 401. Binary Watch

key: ez

3.26.2. 1239. Maximum Length of a Concatenated String with Unique Characters

trick: a great way to do exhaustion for all 0/1 pairs (01010101).

for(n bits)

  for (i = all stored size){

  	stored.push_back(a | b)  // every time push back same size of stored(size x 2) and stored are the all permutations of example.

  }

3.27. tricks

comparison 1 to n, saving possible combinations of 1 and n and do comparing with the saved sets instead of comparing n times.
- 952 Largest Component Size by Common Factor
- 1178 Number of Valid Words for Each Puzzle
- 128 Longest Consecutive Sequence
- 839 Similar String Groupsth
sorting, if get stuck
- 1042 Flower Planting With No Adjacent
- 3sum
hash map(bucket), used to reduce possible results
- 1074 Number of Submatrices That Sum to Target
- 421 Maximum XOR of Two Numbers in an Array
- 336 Palindrome Pairs
other
- %2 => &1 ==1
moore-voting for
- 169
- 1157
discretion
- 850 Rectangle Area II
prefix array (when dealing with times of product/ sum of array )
- 1352

Title:Data structure & Algorithm & Leetcode

Author:Benson

PTime:2019/11/19 - 12:11

LUpdate:2020/04/03 - 21:04

Link:https://steinsgate9.github.io/2019/11/19/datastructure-algorithm/

Protocal: Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) Please keep the original link and author.

1. data structures

1.1. linear ADT

1.1.1. vector

1.1.2. map

1.1.3. stack

1.1.4. heap

1.1.5. bitset

1.2. tree ADT

1.2.1. binary tree

1.2.1.1. binary special tree

1.2.1.1.1. segment tree

1.2.1.2. binary search tree

1.2.1.2.1. vanila search tree

1.2.1.2.2. red-black tree

1.2.1.2.3. avl tree

1.2.1.2.4. splay tree

1.2.1.3. heap

1.2.1.3.1. skew heap

1.2.1.3.2. leftiest heap

1.2.1.3.3. bionomial queue

1.2.1.4. huffman tree

1.2.1.5. binary index tree

1.2.2. general tree

1.2.2.1. B tree

1.2.2.2. B+tree

1.2.2.3. Trie

1.3. hashtable ADT

1.3.1. hash function

1.3.1.1. 直接定址法

1.3.1.2. 除留余数法

1.3.1.3. 平方取中法

1.3.2. hash collapse

1.3.2.1. 开放定址

1.3.2.2. 链地址法

2. algorithms

2.1. optimal search

2.1.1. depth first search

2.1.1.1. tail recursive

2.1.2. breadth first search

2.1.3. dynamic programming

2.1.4. binary search

2.1.5. greedy search

2.1.6. branch & brand

2.1.7. random search

2.1.7.1. local search

2.1.7.2. metropolis search

2.1.7.3. genetic search

2.1.7.4. randomize search

2.1.7.5. greedy search

2.1.8. heuristic search

2.1.8.1. greedy best first search

2.1.8.2. A*

2.2. adversarial search

2.2.1. max min search

2.2.2. \(\alpha \& \beta\) trim

2.2.3. Monte Carlo search

2.3. sort

2.3.1. insertion sort （从左边开始固定）

2.3.2. bubble sort （从右边开始固定）

2.3.3. selection sort （从左边开始固定）

2.3.4. merge sort

2.3.5. heap sort

2.3.6. count sort

2.3.7. bucket sort (improved count sort)

2.3.8. radix sort

2.4. graph

2.4.1. topological sorting

2.4.2. union find

2.5. string

2.5.1. rolling-hash

2.5.2. largest suffix

2.6. stats

2.6.1. moore-voting

2.6.2. Random Generator

2.6.3. Fisher–Yates shuffle

2.6.4. Reservoir Sampling

2.6.5. random number

2.6.5.1. add mod

2.6.5.2. linear mod

2.6.5.3. non-linear mod