Combinational Optimization Course Slides Notes
1. linear programming
1.1. linear problem types
Def: linear programming


Def: standard form of linear programming

Def: totally unimodular

Qua: => relaxation=integer

1.1.1. integer programming
Def: Integer programming

Qua: NP-hard
Proof:
idea:
partition <=p integer
partition: given $ { a1,a2...an }$, let some of the instances = half of sum
integer programming: $ {n = 1}^{}aixi=1/2 {n = 1}^{}ai$
prove that integer is np
if the programming have a solution, then O(solution) = poly(input)
Def: mixed integer programming
some of ... is integer
Def: o/1 programming
all x is 0/1
1.1.2. relaxation
Def: relaxation
Qua: => constraint have to be met in optimal solution
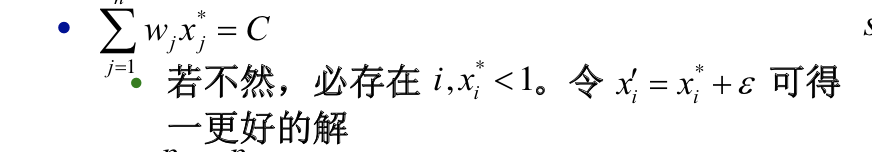
Qua: domainI(IP) <= domain(LP)
Qua: solu(IP) < solu(LP)
Qua: best(IP) <= best(LP)
Qua: if the A = totally unimodular, then best(IP) = best(LP) (totally unimodular quality)
1.2. solution to linear programming
1.2.1. general procedure for solving
Def: general procedure for solving linear programming
1.2.2. linear programming method
1.2.2.1. simplex method
Def:
- problem:
Qua: exponential some times but faster in general
1.2.2.2. graphics method
Def:
- problem:
Qua: multi-linear, but almost always slower
1.2.2.3. cutting plane method
1.2.3. search-based method
1.2.3.1. computer theory
- divide and conquer (make a tree and search it)
- pruning(backtracking )
1.2.3.2. implementing techs
- recursive
- incursive
1.2.3.3. method
1.2.3.3.1. bfs
Def:
intro: one of basic search algorithms( way to be more specific)
problem: search(opt) / tranverse(decision)
1.2.3.3.2. dfs
- Def:
- intro: one of basic search algorithms( way to be more specific)
- problem: search(opt) / tranverse(decision)
1.2.3.3.3. backtracking
Def:
intro: dfs + pruning
problem: search(opt) / tranverse(decision)
1.2.3.3.4. dynamic programming
Def:
intro: dfs + saving ( turn into bottom-up algorithm instead of top-down search or a smaller structure of the dfs tree)
problem: opt
Theorm: principle of optimality

Note: This therom gives the function below and give the propagation function,
the propagation function iff exists the principle of optimality holds + subproblem overlap
And it derives the (top-down / bottom-up optimization of DP) \[ best(s1,n) = best(best(s1;s2,n)) \]
Note: how to choose subproblem

Def: subproblem map
Usage: can be used to visualize the overall propogation equation

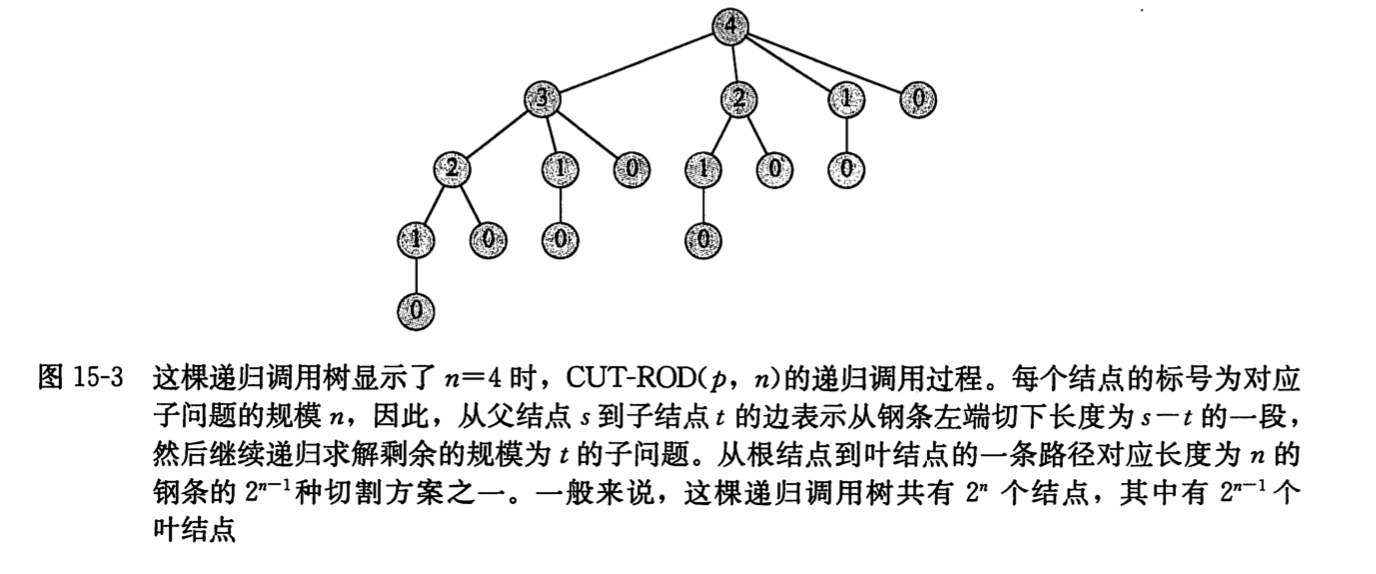
Note: we can use this map, compute the edges of this map, and get the complexity.

Def: 2 ways of implementation

1.2.3.3.5. branch & bound
Def: for maximum problem
intro: bfs/dfs + trimming
problem: opt
Qua: exp algorithm
Algo: for max problem
Usage: for each branch we have upper bound (possible largest result), if upper bound < lower bound (alread results), we trim。


for min problem

Note:
lower bound=existing solutions, upper bound is for every branch
if upper bound < lower bound, then prune the branch
for 0-1 variable, 分支 is trivial since you always 分 0/1
1.2.3.3.6. greedy search
- Def:
- intro: bfs/dfs + greedy choose
- problem: opt
1.2.3.3.7. A*
- Def:
- intro: bfs + inspire
- problem: opt
1.2.3.3.8. B*
Def:
intro: bfs
problem: opt
1.2.3.3.9. D*
1.2.3.3.10. IDA*
- Def:
- intro: dfs + inspire
- problem: opt
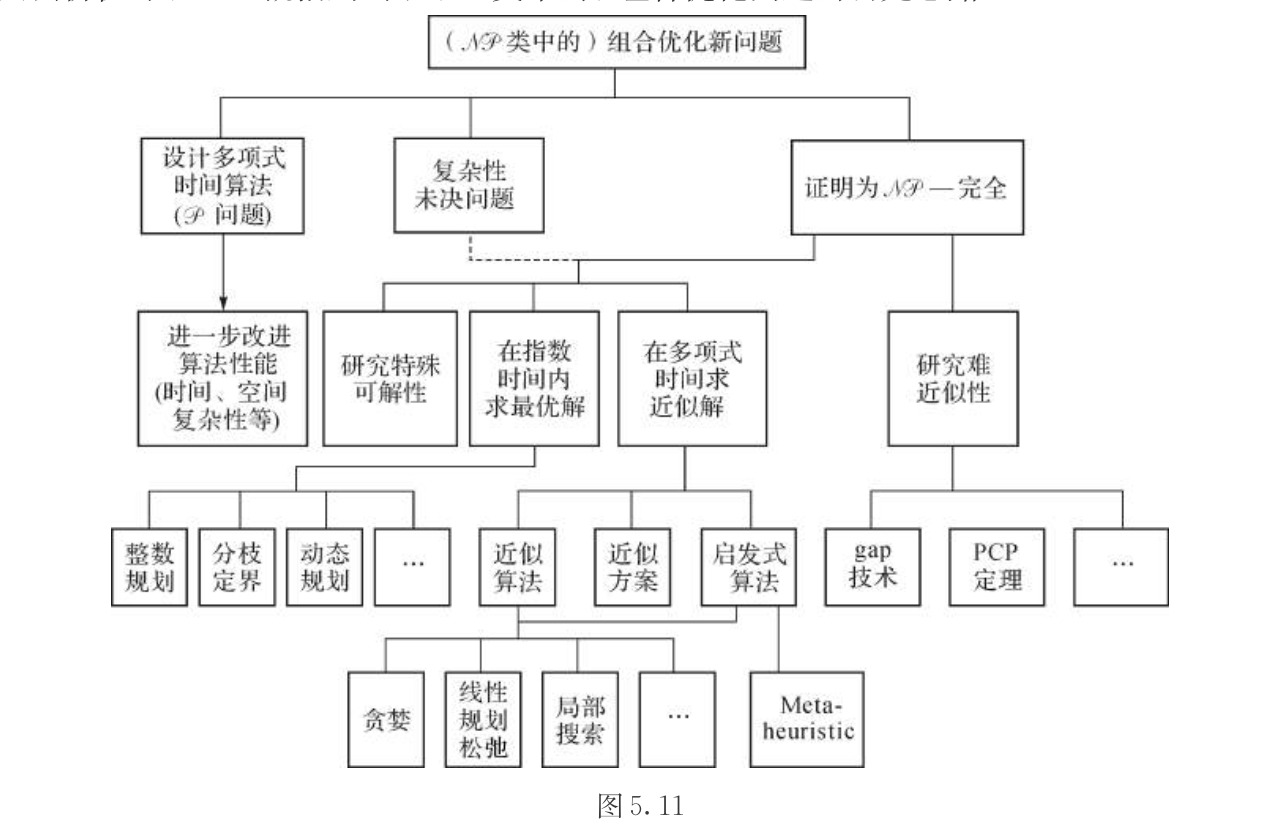
1.2.4. approximation method
1.2.4.1. computer theory
local search
greedy
relaxation
1.3. specific question
1.3.1. subset sum
Def: decistion form

Note: opt form, is a subproblem of backpack
maximum

minimum
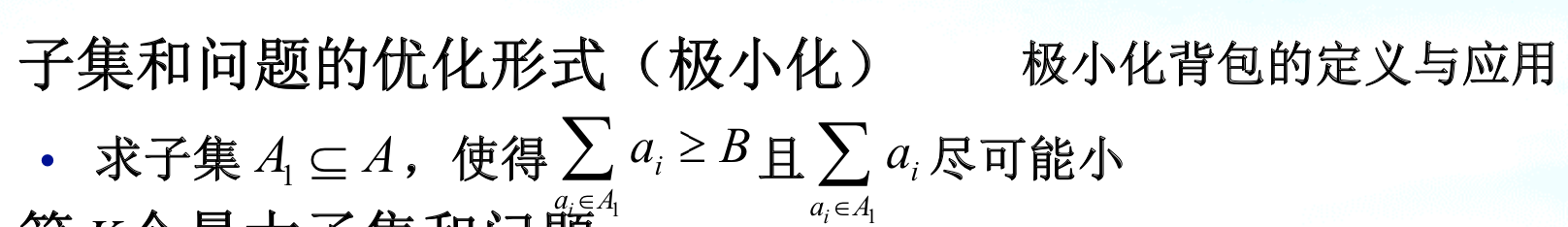
k-subsum

1.3.2. backpack problem
Def: 0-1 backpack problem

1.3.2.1. dp1
Algo: dynamic programming


Qua: O(nC), pseudo-poly algorithm( if max number C is bounded by O(2^n), then the DP is polynomial, this is the definition of pseudo-poly)
the input is n+logL, L = max(max pj, max wj, C)
1.3.2.2. dp2
Algo: dynamic programming 2


- Qua: O(nP), same as above
1.3.2.3. branch & bound
Algorithm: relaxation linear programming ( branch & bound method )
properties for relaxation problem

UB1: we use relation problem tp compute upper bound for non-relaxation, a fixed one, not optimal since we want it to be small.

UB2: we optimize the UB1
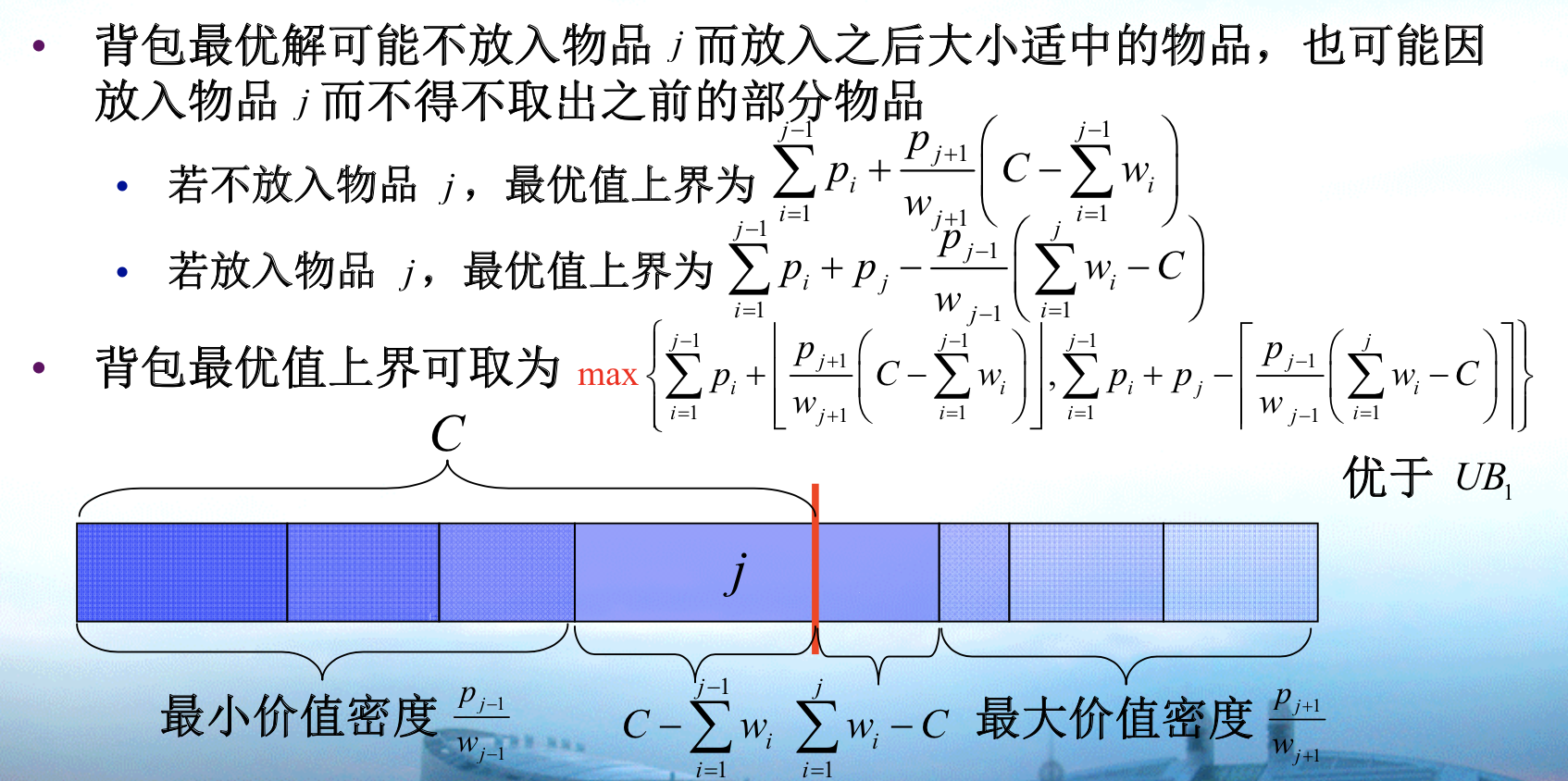
LB1:
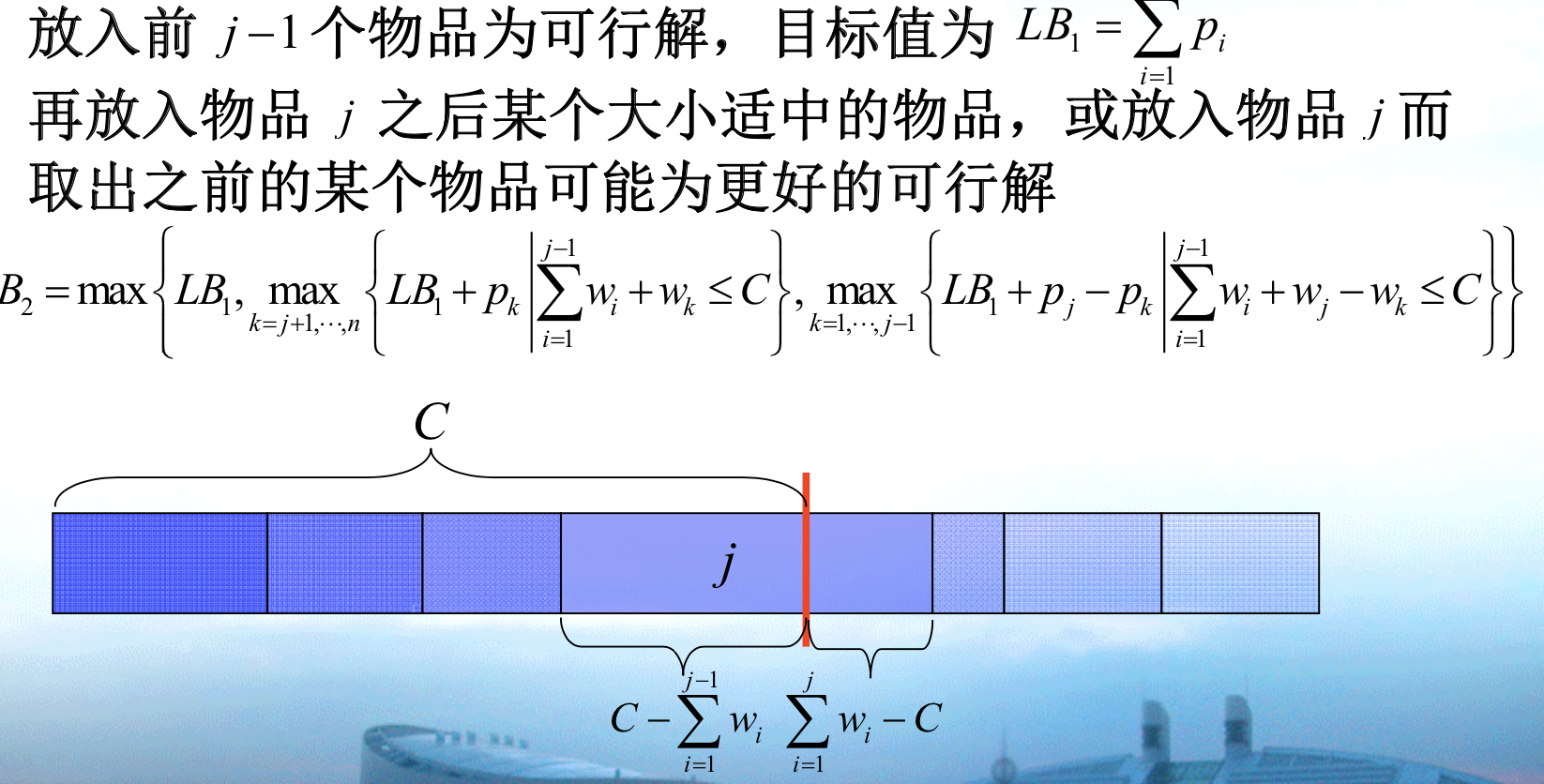
Qua: => some constraint relaxation programming have to obey

1.3.2.4. greedy
Algorithm: greedy

Note: the approximate ratio is \(\infty\), so we have to improve it
1.3.2.5. improving greedy
Algorithm: improving greedy method

Qua: the approximate ratio is 2
Proof: using a upper bound (UB1)

1.3.2.6. PTAS
Algorithm : PTAS
Usage: ensembling \(2^k\) possible solution together and output the best of them. 1) design a feasible bu t not optimal greedy solution 2) k is used to bound time & maximize capability of greedy solution.

Proof: separate the JK into 2 part by i0. the first part consist only intersection & jk itself, because no samples exists only in J* before i0. the second part consist of 3 part. This construction is done by introducing i0, have nothing to do with Jk algorithm(only Jk indicate that Ja+beta is not empty since i0 can't be the largest )

Note: this is a greedy solution. Key point of proof is Jkf have lower bound \(\alpha + \beta\), and use that lower bound with conditions provided by \(i_0\)(密度&重量), we can finally prove the point.

Note: fig
IMG_4922
1.3.2.7. FPTAS
Algorithm: FPTAS
Note: how to design a FPTAS => 1) design a unfeasible solution and make constraints 2) t is used to bound poly run time & reduce MAX of instance(maximize the capability of DP in another way by making it feasible).

Proof:

Note: 从一个伪多项式算法出发,设计一个P缩微的实例。(之所以不放C,是因为可行性有可能改变)从这个实例出发,从左上到右上到右下到左下,右上右下都是天然下界。
1.3.3. assignment problem & TSP
Def:assignment problem


Note: standard form
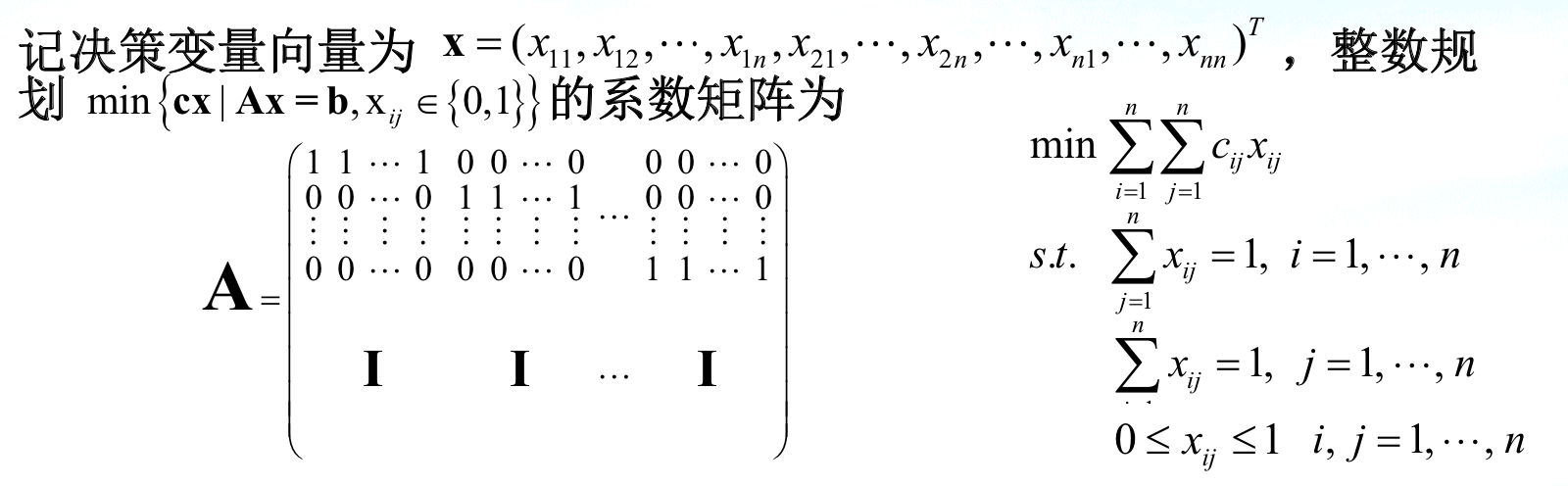
Qua: P( special kind of integer programming is poly solvable, NP-hard is defined when n->inf)
Qua: equivalent to Bipartite Matching

Qua: standardization, A is shown above, A is totally unimodular matrix
1.3.4. tsp problem
Def: tsp problem (same as assignment ) (this is not the final version)

Note: sub-tsp have to be mentioned. sub-tsp have to be mentioned, the problem can be separated into several small problems if the constraint is not mentioned.
Qua: first solution
Proof: since the only 2 conditions are: from 1 -> 1 / 1-> 1 + j -> j, we eliminate the second condition.

Qua: second solution
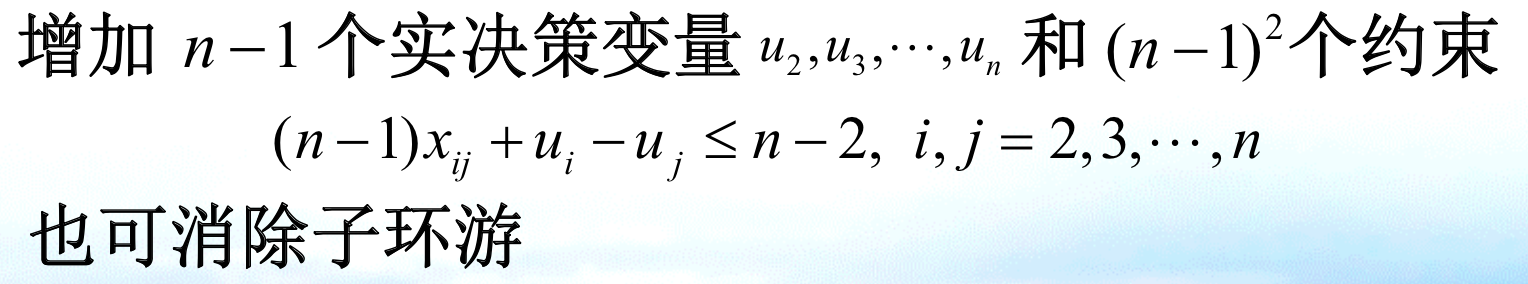
Proof: note that the given condition makes that every
=>

<=

Qua: NP-C
Qua: no constant - ratio

Proof: using reduction to HC, which is a NPC problem, (gap technique)

Qua: no FPTAS
1.3.5. metric TSP
Def: metric tsp

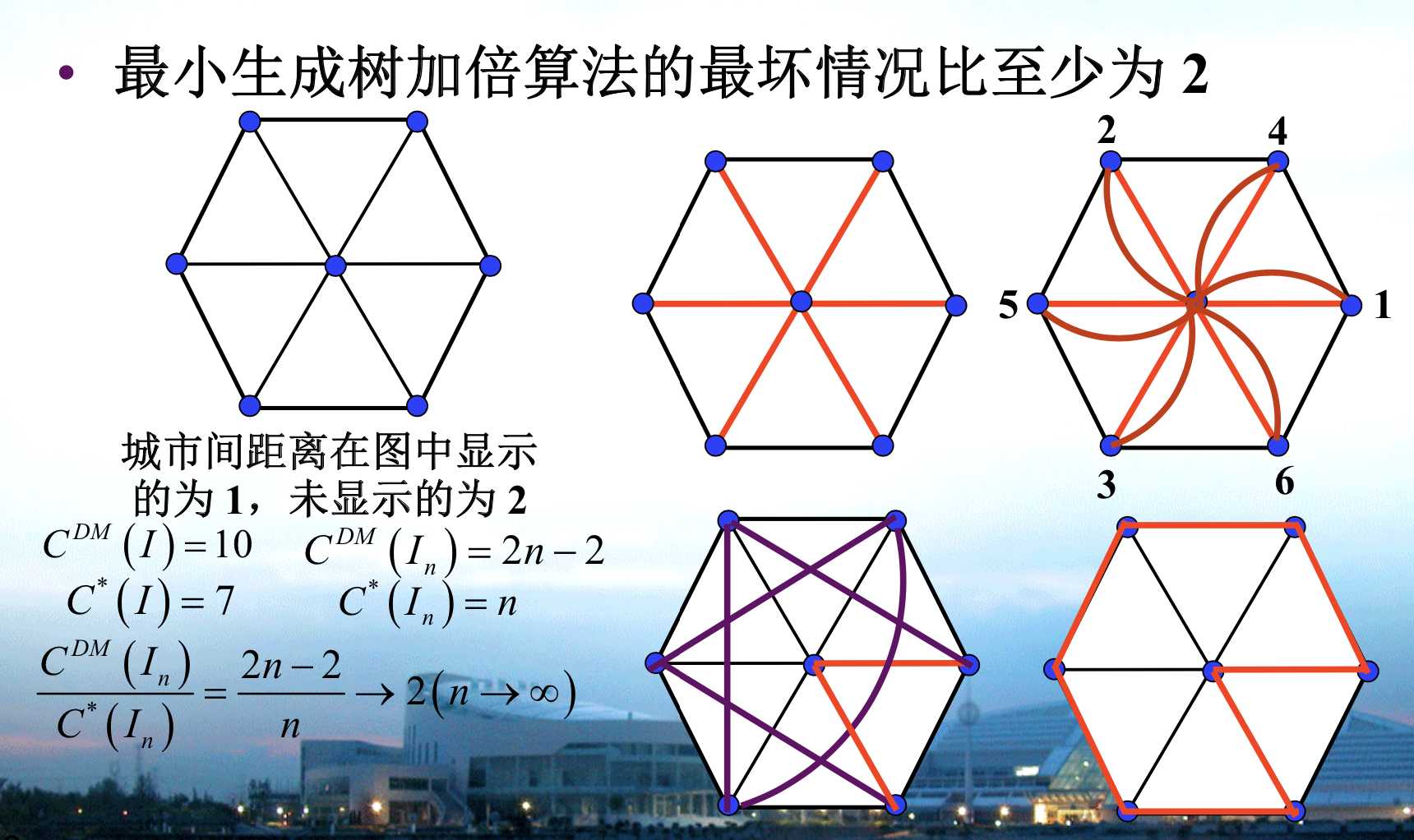
1.3.5.1. spanning tree
Algorithm: weighed smallest spanning tree method

Qua: => appximate ratio = 2

Proof: we need to prove that 2xtree will always suffice to make it larger than Cdm. By that I mean the edges will always be enough to eliminate edges in Cdm. since the degree of nodes can't be three, we proved the point.
Note: Lt act like a LB for C*.

Qua: => the best approximate ratio = 2
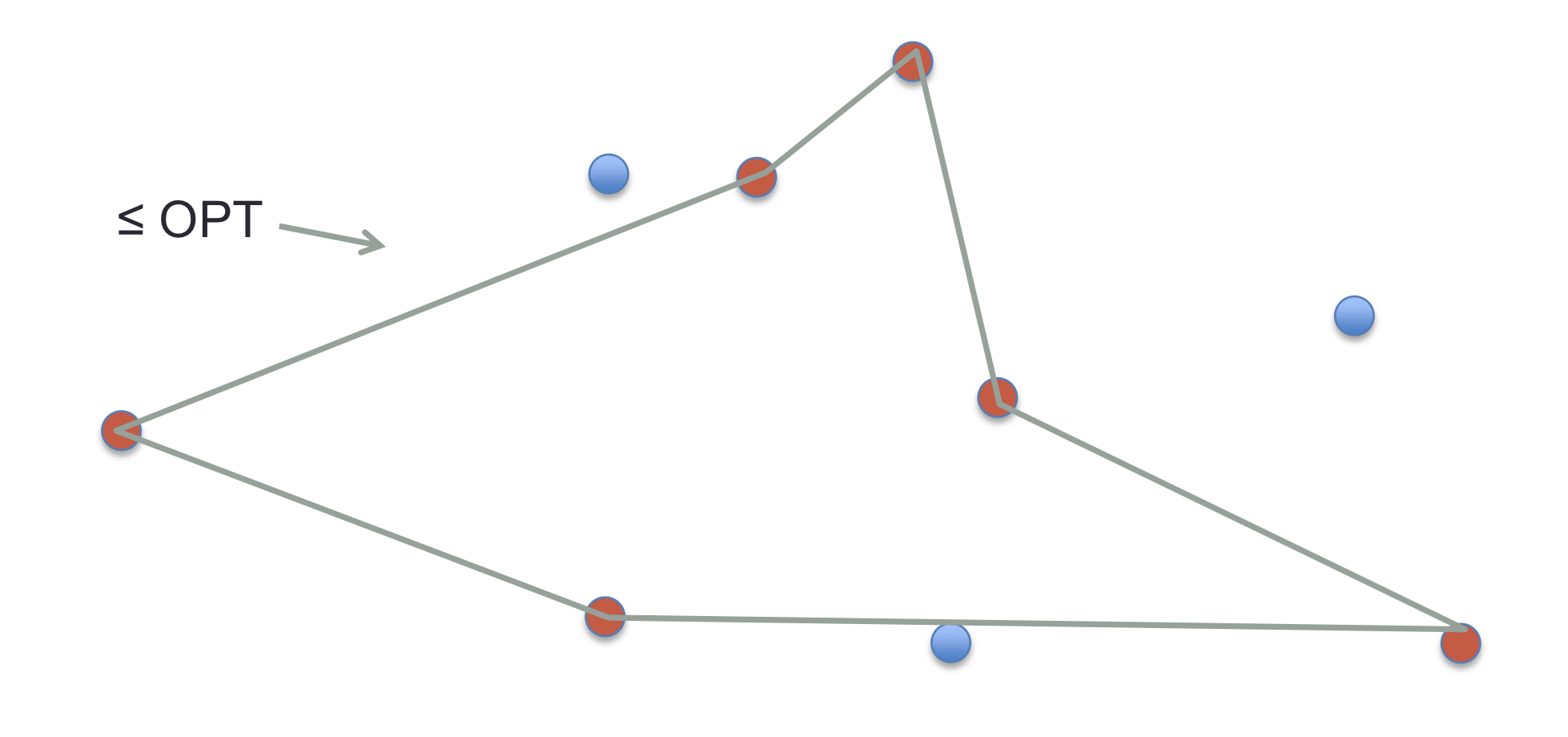
Proof: given an example of worst ratio
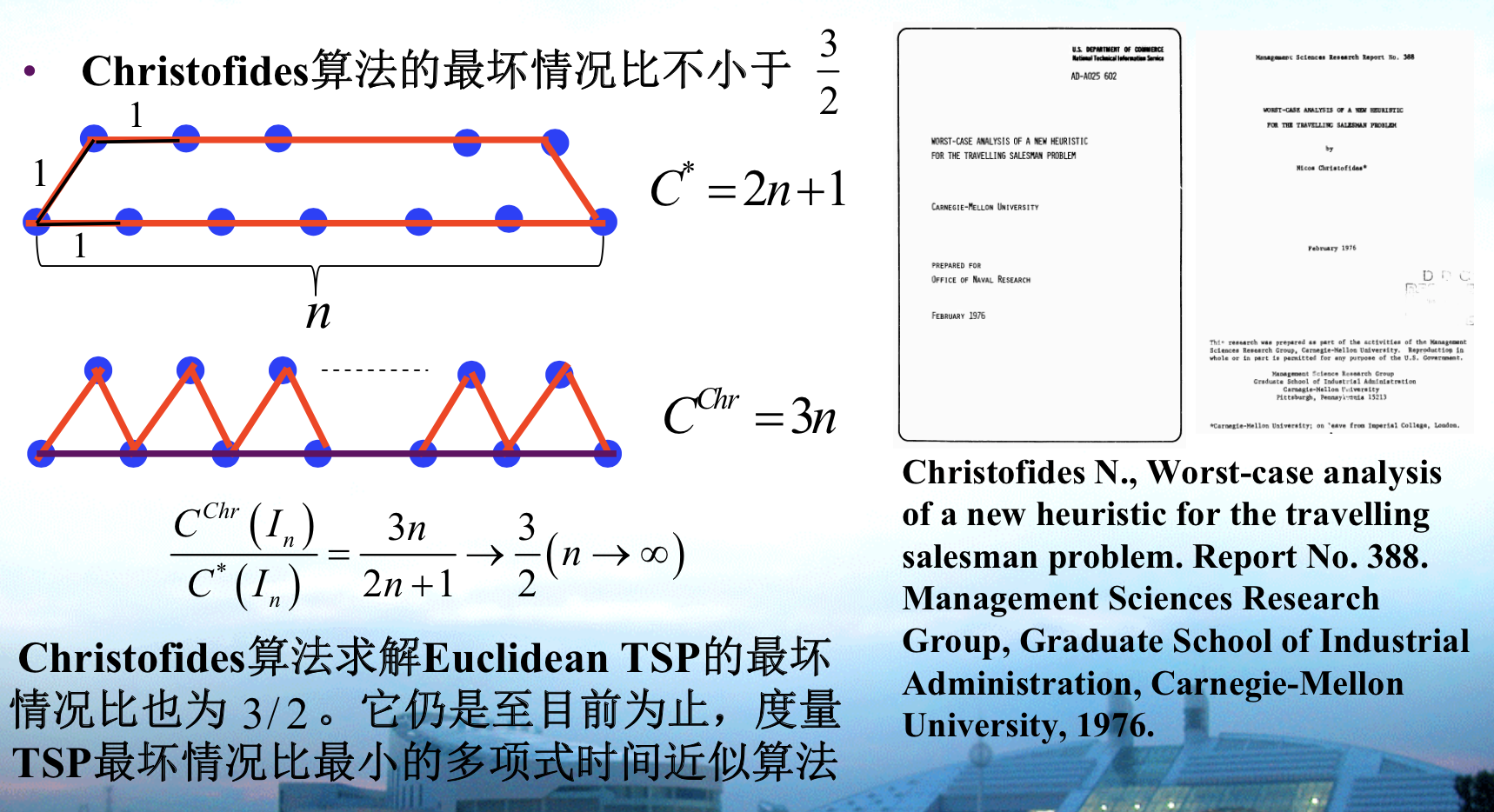
1.3.5.2. christofides
Algorithm: christofides
Usage: note that euler tour can be redundunt on edges as long as you past every edge in the M+T

Qua: => ratio \(\leq\) 3/2

Proof: first we prove that T< C, this is easy since we can erase edge from C and T<C-edge<C. Then we can see that Chr = M+T - Euler overlap < M+T < M + C. And C > C - evenpoint >= 2 * M . So M<=C/2, Chr< 3/2 C.
Note: C- evenpoint, and this is the lower bound of C which is very important.
Qua:worst ratio \(\geq 3/2\)
1.3.6. shortest path
Def: given

1.3.6.1. Dijkstra
Algorithm: 3 classic basic algorithms

Algorithm: Dijkstra, no negative weight, from 1 point to other point
1) choose a point with the smallest dis
2) choose the nearest neighbor ( smallest cj)
3) update all point cj
4) set the point as updated()
Proof: proof is easy, but note the proof involves in trimming those larger than local smallest, this can not be used in longest path. You can see that the trimming actually trimmed other edges from updating other than the 'fixed' set. The conditions are \(c_ {ij} > 0\). However in longest path, if and only if pj is non-increasing, or \(c_{ij} <0\), this algorithm can be used. \[ p_j = min(p_{smaller set}+cij) \\ p_j \text{ is non-decreasing} \]
Note: actually a top-down implementation of bfs, using the feature of principle of optimality, 感觉像是DP算法的进一步优化版本,DP算法尽管有重叠子问题可以消除,但是dij算法还去掉了一些重叠子问题减少计算量(比如在第二个点固定的过程中就只考虑了第一个点的update,其他点都去掉了)
Note: we can generalize the DP algorithm by fixing node by node.
1.3.6.2. Floyd
Algorithm: Floyd,
D[i][j][k] means the the smallest distance between i and j considering only [1:k] nodes in bewteen 1) go from k = 1 -> n
2) update i & j (at kth level )
Proof: when k = m, you can prove that with m nodes in between, the update is valid. If not, after the update, there exists some node gg $$ [1, m], and \(i^*\to gg + gg \to j^* < i \to gg + gg \to j\) , so that either i->gg or gg->n is not the smallest path.
Note: intuition is if left is shortest path and right is shortest path then the middle is shortest path. we can generalize the DP algorithm by fixing layer by layer such that the update path only concerns k nodes.
Qua: note that shortest path satisfy DP \[ r_i = \min \limits_{j \in N(i)} (P _{ij} + rj) \]
Proof: 1) when u->w->v and p'(u->w) is a shorter path than u->w, if p' have no overlap with w->v ,we simply replace u->w with p'
2) when u->w have overlap with w->v, we replace with u->x & x->v where x is the overlapping point.
Note: that longest path can't prove by this procedure since u->x & x-> v is shorter not longer.
1.3.7. take-out problem (specific shortest path)
Def: a special form of shortest path,


1.3.7.1. dp
Algo: dynamic programming


implementation( here min should be max and wjt = max里面的内容 )

Note: use special form of Dij algorithm to solve it. You can see that rj is non-increasing/ 直接加两个负号,-ri = min(-ri+l1)变成最短路问题(最短路问题l1验证必须为正)
1.3.8. minimum matching
Def: minimum matching
Usage: matching 问题简而言之就是找一个边集,使得任意顶点只有一条边。

1.3.9. vertex cover
- Def: vertex cover


Qua: NPC
Proof: 3SAT \(\leq p\) VC
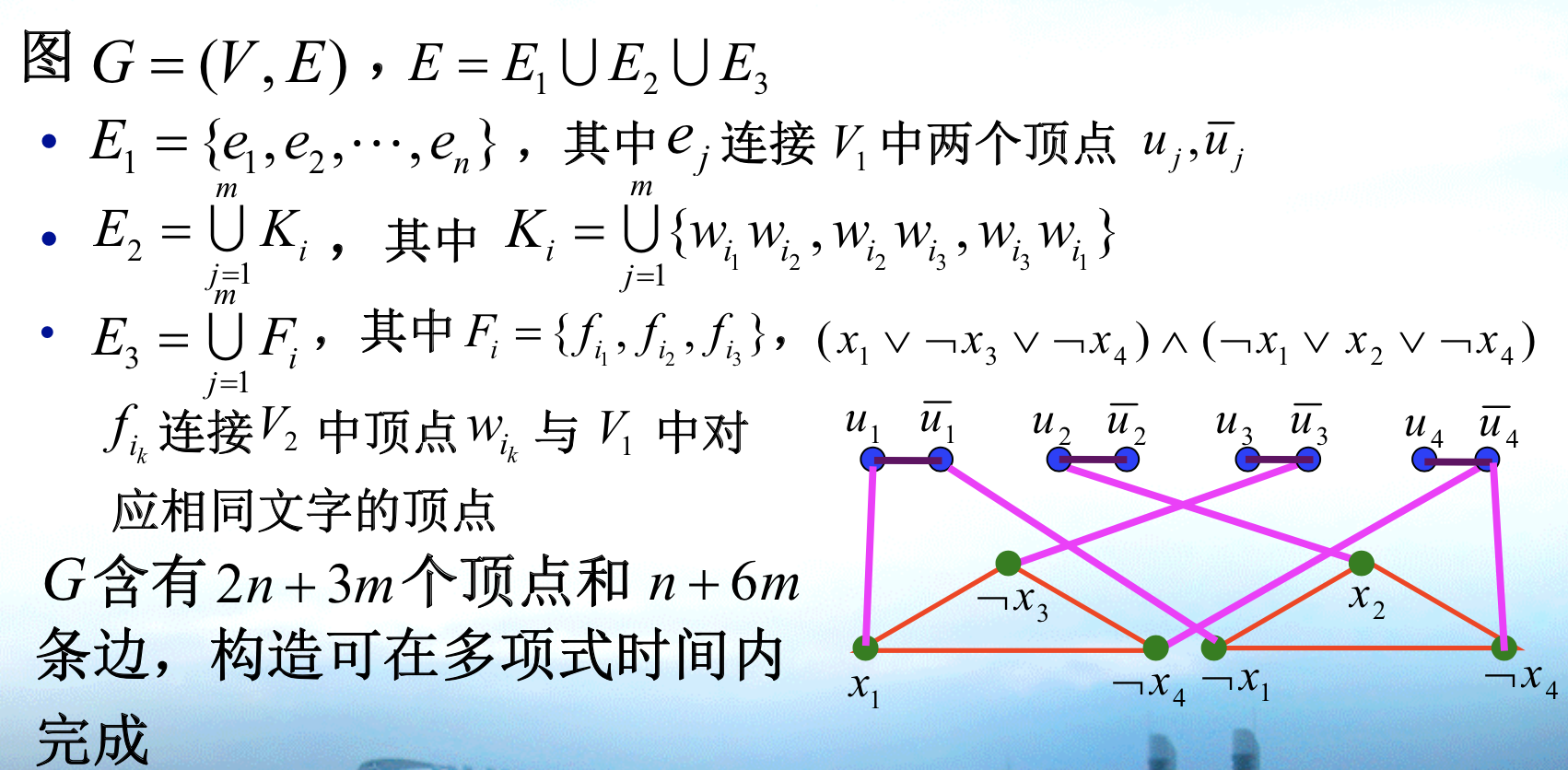
=> 通过给=1的顶点染色,然后给剩下三角形的两个染色,证明是VC
<= 先证明如果是VC上面必须有n个,下面也必须有2m个,又因为条件里有《n+2m,所以=n+2m个,然后就证完了。
1.3.9.1. relaxation algorithm
Algo: relaxation algorithms
Qua: => ratio \(\leq\) 2
Proof: LP is natural lower bound.

1.3.10. partition problem
1.3.10.1. subset partition
Def: partition problem
desicion version

opt version
1.3.10.2. product partition
Def: product partition problem

Qua: NPC, have FPTAS

1.3.11. scheduling
Def: scheduling problem
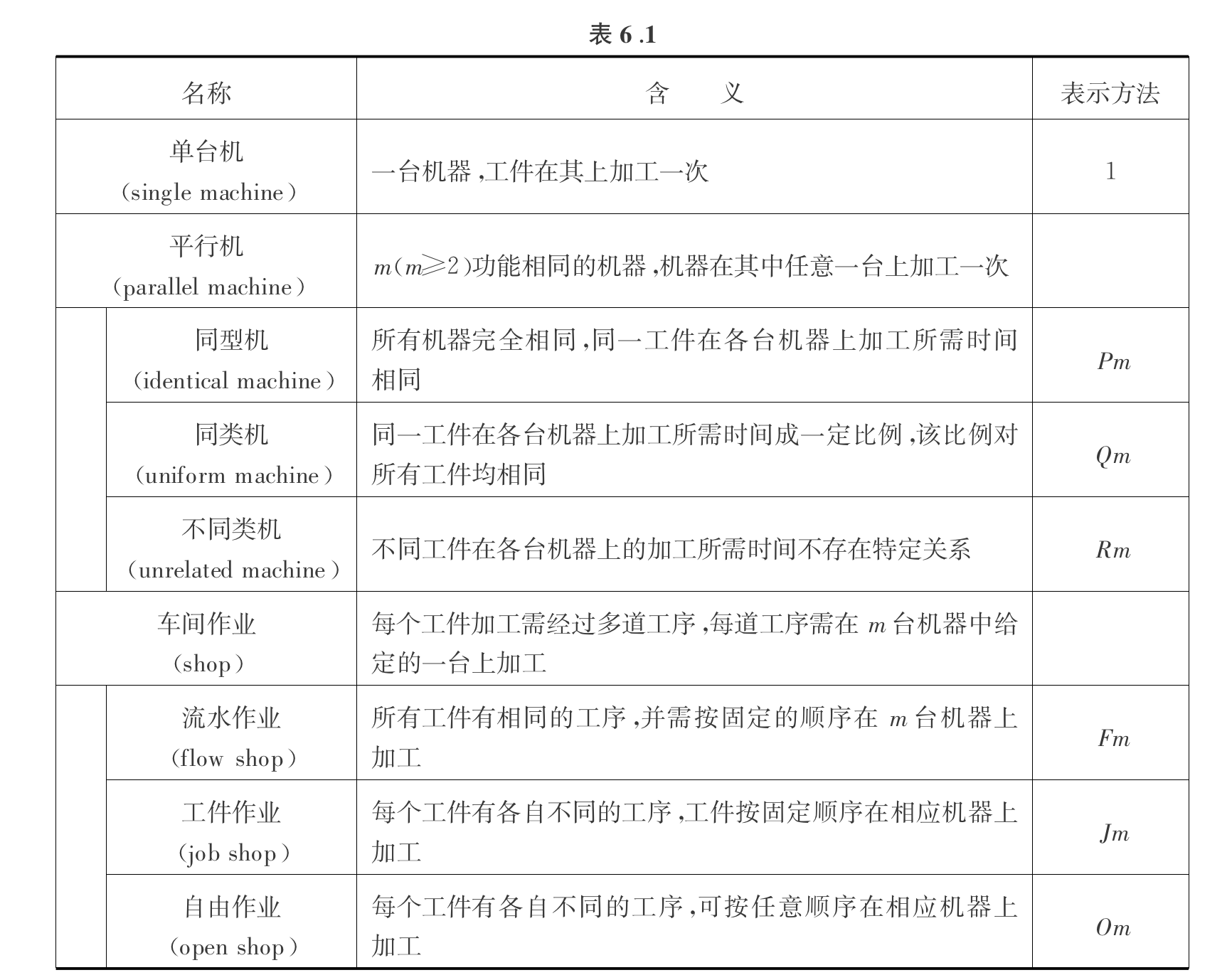
Usage: representing scheduling problem in 3 elements



Def: machine env ( \(\alpha\) )

Example: possible example of machine environment, note that parallel have no bounds on machine sequence, it's more like to make things more equal. And shop have bounds on sequences and shit have to be on multiple machines, it's more complicated.
Note: mixed & hybrid
Def: job characteristic ( \(\beta\) )

Note: more constraint

Def: loss function ( \(\gamma\) )


Def: gatt diagram
Usage: representing a possible solution
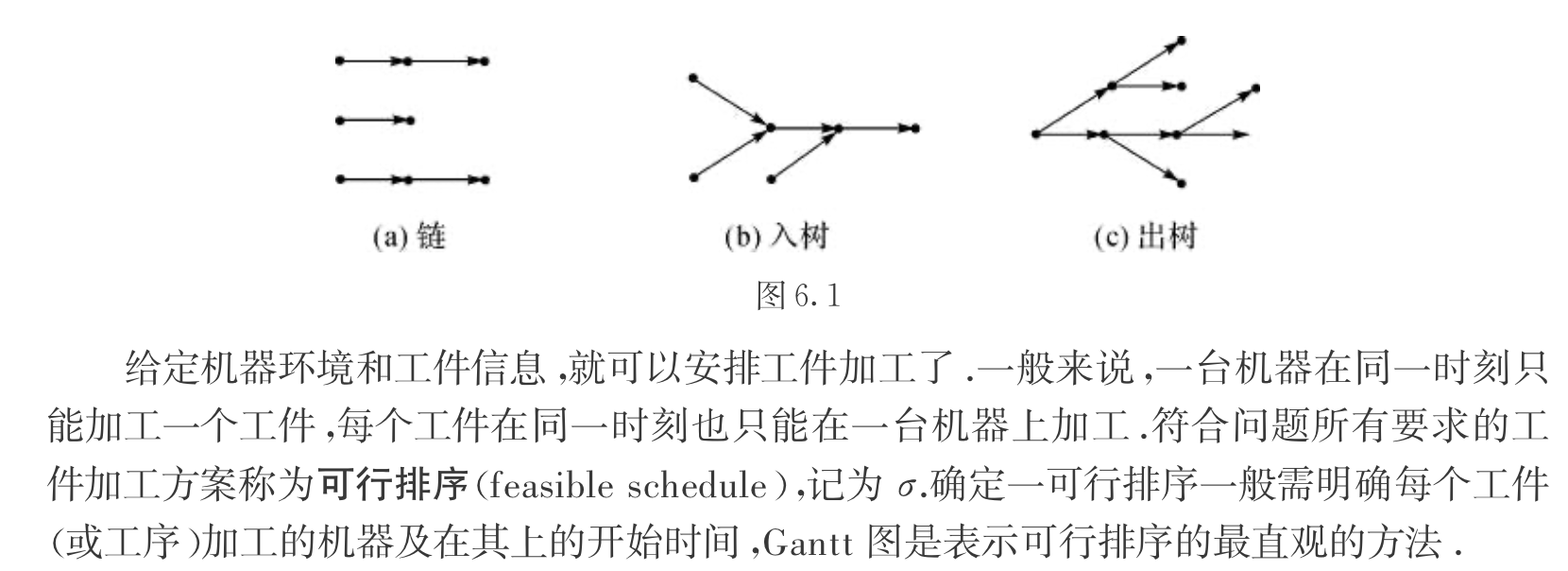
Example: Santa problem
Usage: the simpliest scheduling problem ( without precedence )

Example: parodox of scheduling problem
Usage: the cons for greedy algorithms: decrease job time & increase machine number will not necessarily yield better result.
P175
1.3.11.1. P1 Cj, Cmax, L1max, Tj, Uj
1.3.11.1.1. \(C_{max}\) or \(\sum_{n=1}^{\infty} C_j\)
Def: \(C_{max}\) or \(\sum_{n=1}^{\infty} C_j\)
Algorithm: for \(\sum_{n=1}^{\infty} C_j\): SPT

Algorithm: weighed sum cj \(\sum_{j=1}^{n} w_jc_j\)
Note:
0.0) \(\sum_{n=1}^{\infty} wjcj = (w_1+...w_n)p1 + ...\)
1.0) when n = 2, get solution \(w_2p_1\) vs \(w_1p_2\)
2.0) when n > 2, insights from n =2, sort \(\frac{pj}{wj}\)
Proof:
1.0) swapping 2 element i,j => contradiction,
1.1) set i - j =-1 to make it easier.( this step is important since we only get information from i and j)
Algorithm: weighed functional sum of cj : \(\sum_{n=1}^{\infty} w_jg(c_j)\)
Qua; when g is convex: worst ratio = sup ...
Qua: when g is 分段linear: NPC
Qua: when g is \(x ^{\beta}\) => i <g j & i <l j
1.3.11.1.2. L1max, Tj, Uj
Def: one machine problem: \(L_{max}\) is the maximum of delay time. \(\sum_{n=1}^{\infty} U_j\) is the total delayed objects. $ _{n=1}^{} T_j$ is the added delayed time.

Algorithm: for \(L_{max}\): EDD
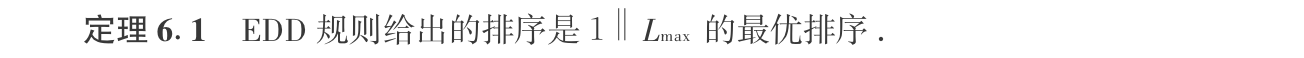
Proof: By contradiction. Note that we only need to prove \(L_{max}\) is not increasing, and only k, j, i changes in the \(\sigma'\) solution and everyone of them are bounded by the max($$) of the original.


Algorithm: for \(\sum_{n=1}^{\infty} U_j\) : Moore-Hodgeson(EDD improve)

Note: example of Moore-Hodgeson
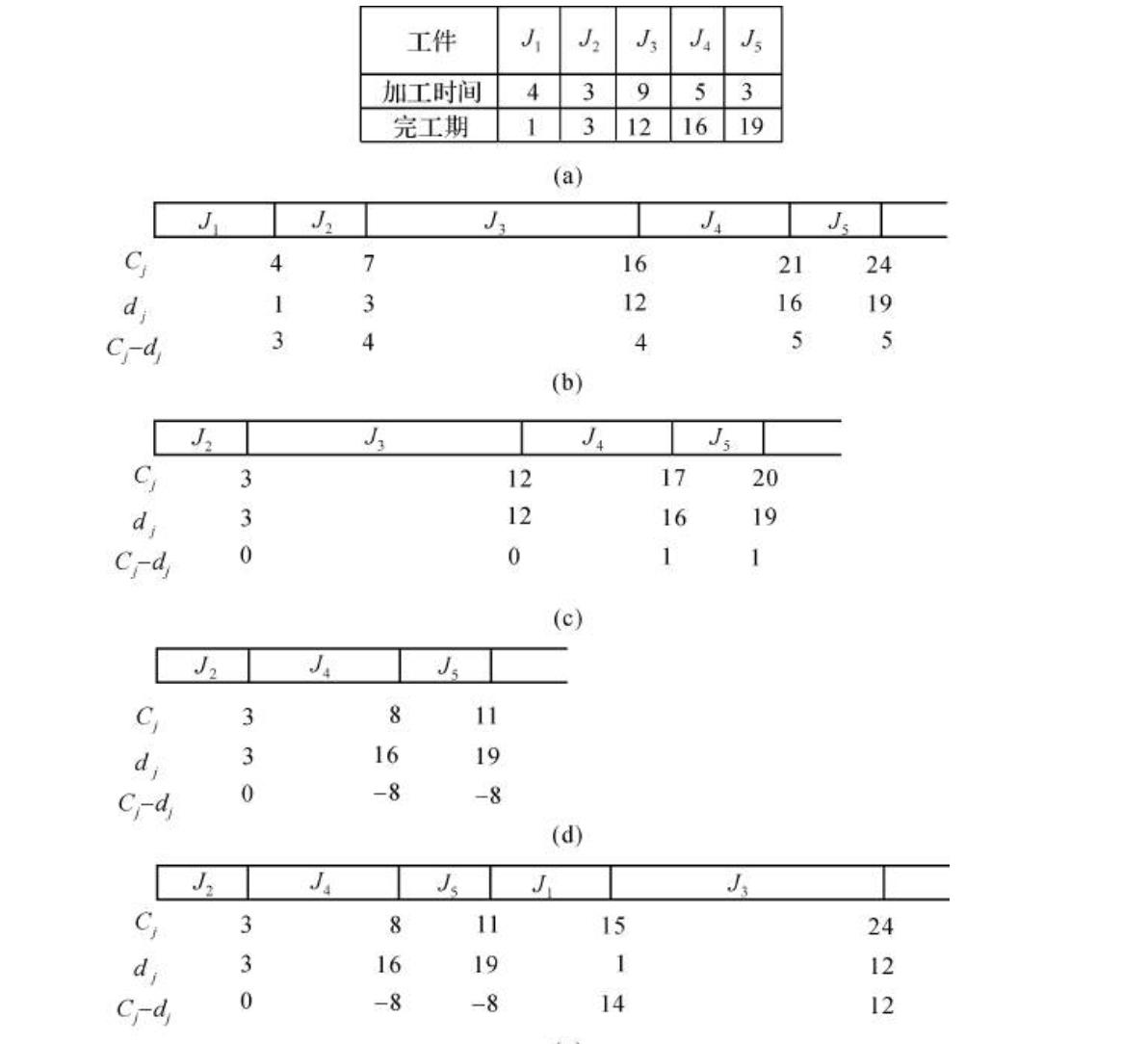
Algorithm: for \(\sum_{n=1}^{\infty} T_j\)

Note: no resting time
Qua: => exist pseudo - p algo
Qua: => exist FPTAS
Qua: => NP-C
Algorithm: another loss function where we want "JUST IN TIME" : \(\sum_{n=1}^{\infty} T_j +E_j\) where \(Ej= max(d_j-c_j, 0)\)
1.3.11.2. Pm Cmax, Cmin
Def: multi-machine problem Pm
Note: Pm and P difference: whether m is a given input(P) or constant(Pm), the consequence of this is that when Pseudo-P algorithm in Pm is O(P^m), it is exponential in P since m is input.

Qua: lower bound for \(C_{max}\) \[ C_{max}\geq \sum_{i=1}^{n}p_i /m \\ C_{max} \geq \max \limits_{i=[1,n]} pi \]
Qua: => NP-hard
Proof: obvious

from 2 to Pm|| ..: adding p-2 dummy node with cj = C
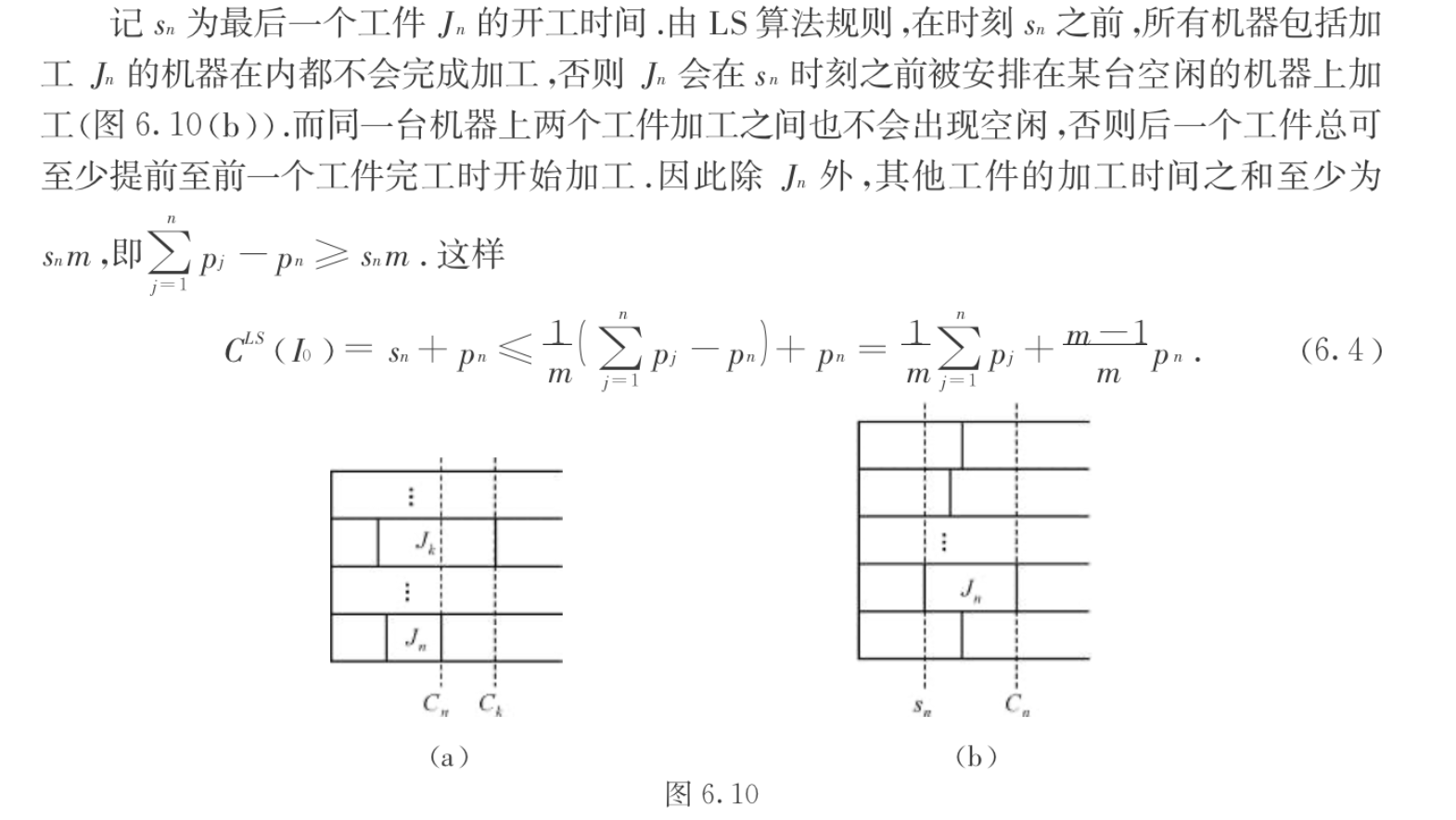
Algorithm: LS
Note: the most important thing is when \(j_i\) is placed on m machine, then other machines are not ready. \(\sum_{i=1}^{n-1} p_i \geq s_nm\)

Qua: worst ratio \(=\) 2- 1/m

Proof: By contrast & minimal conter example: extra information by introducing minimal counterexample instead of counterexample.
1)first prove that Jn determine max span: exactly why we introduce minimal conterexample, this is intuitive since you can always cut the final element if the final element does not decide max span.
which means \(Cls(I0) = s_n + p_n\)

2)then prove by lower bound of C*
3)tightness prove: find an example that have 2 - 1/m: consider LS's con, LS can fill in small items to small which makes things worse.

Note:

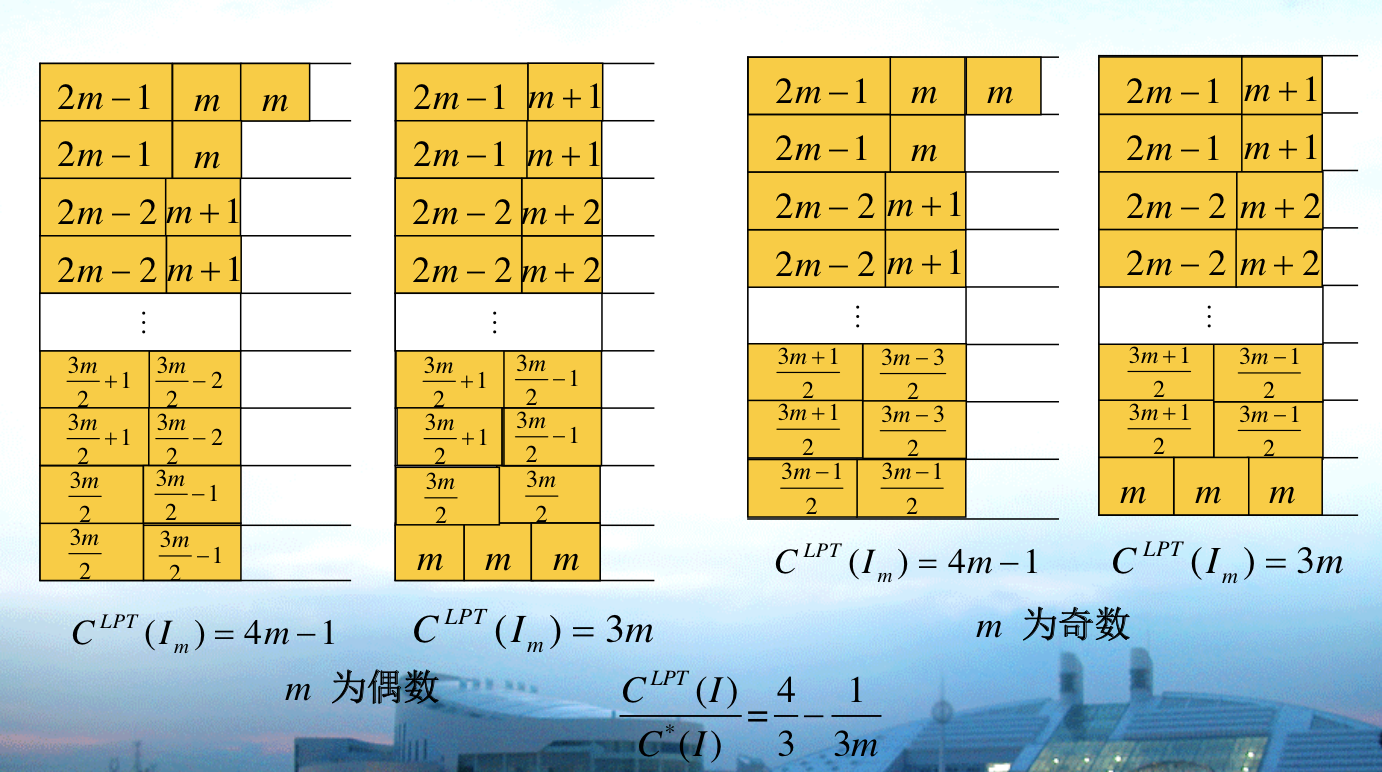
Algorithm: LPT(sorted LS)
Insight: from the worst case of above, that we do from large -> small this time.
Note: note that the additional information is \(C^*(I) <3p_n\) => each lane has at most 2 items, since \(p_n\) is the smallest item

Qua: worst ratio

Proof:
1)LPT can exclude \(C^*(I) < 3 p_n\), that if it suffice, at most 2 items is on each lane in optimal solution. So that leaves us \(C^*(I) \geq 3 p_n\)


2)By construct, construct a LPT solution by transforming a optimal solution( one on one relationship between LPT with some optimal).

3)tightness proof
Def: Pm||Cmin (maximization problem)
Algorithm: LS
Note: LS gives us \(L_i- p_{j_i} \leq L_m\)
Qua: worst ratio = m

Proof:
1)prove ratio $ $ m
1.1) By provided condition: first prove lower bound for Cls: Lm

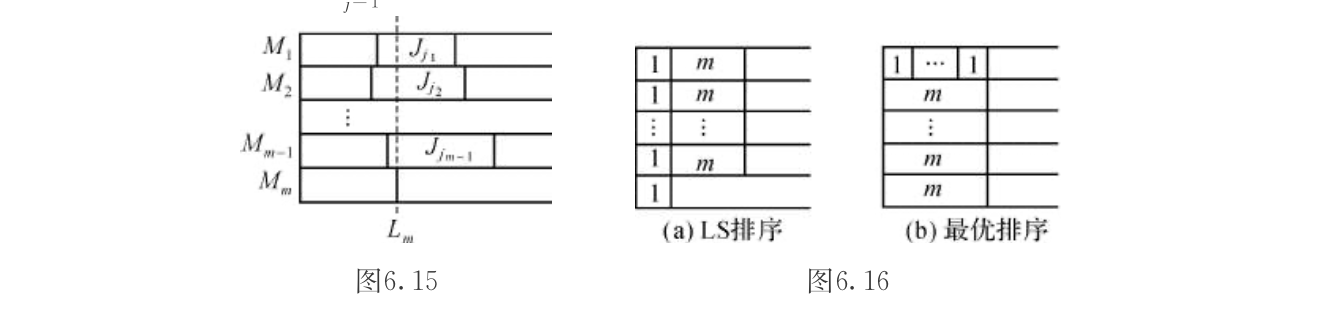
1.2) By contradiction, second prove upper bound for C*

2)ratio \(\geq\) m, same as LS Cmax, but swap 1 & m
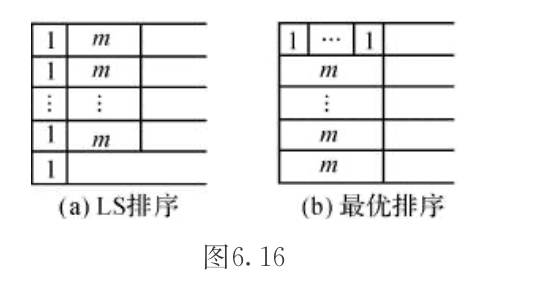
Algorithm: LST
- Qua: worst ratio = \(\frac{4m-2}{3m-1}\)
Qua: for every instance, there's not always a scheduling that satisty both optimal for Cmax & Cmin. But is there an algorithm such that ratio_min < \(\alpha\) and ratio_max < \(\beta\) ?

1.3.11.3. P Cmax
Def: P||Cmax
Qua: strong NP-hard
Proof: 3-partition $ _p $ P||Cmax
Note: Pm||Cmax can not use this reduction since m in Pm is a constant .
1.3.11.4. F2 Cmax
Def: F2 Cmax

Algorithm: Johnson
Note: why sort the second array?

Note: fig
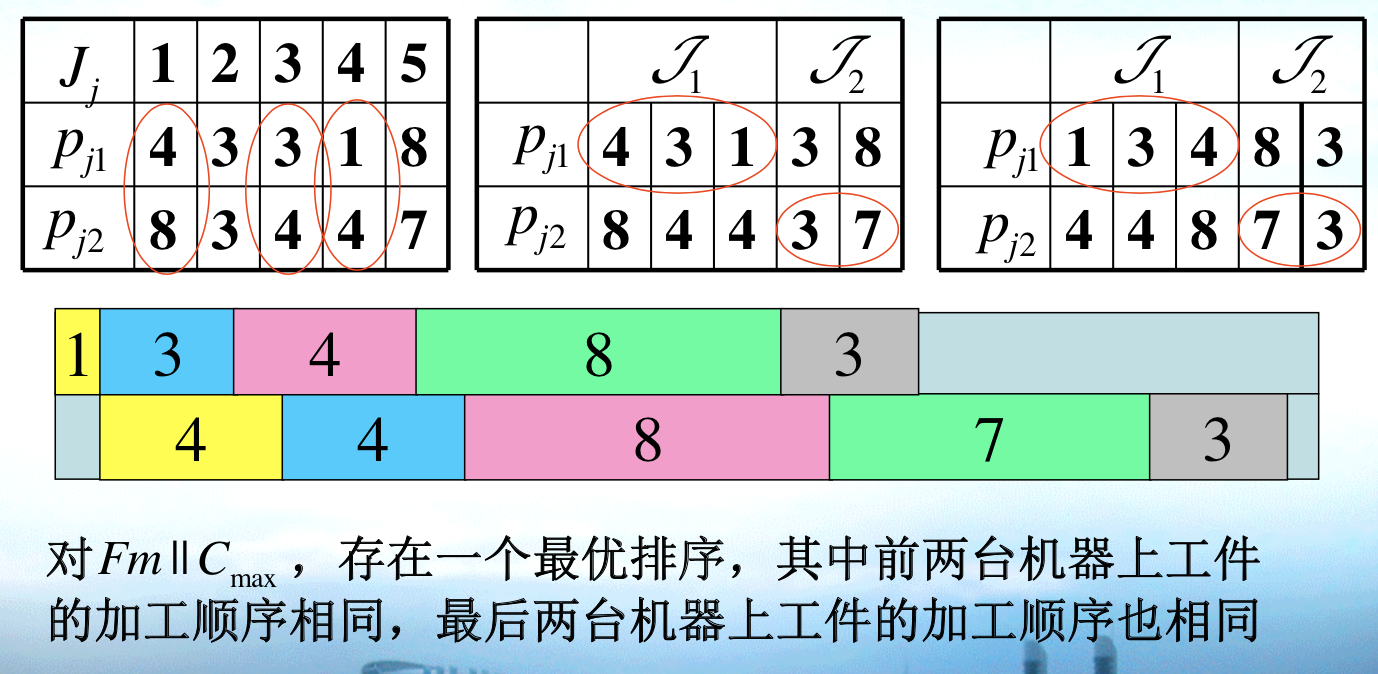
1.3.11.5. F3 Cmax
Def:
Qua: worst ratio <= 5/3 or 3/2

1.3.11.6. Fm Cmax
Def:
Qua: possible lower / upper bound
Note: LB = max{dilation, congestion}. dilation = $max {j=1}^{n}pji $ , congestion = $max {i=1}^{m} pji $
dilation is the max sum of item since every item have to finish all routine, congestion is the max sum of machine since machine have to finish given work.

Qua: exists PTAS

Qua: worst ratio > 5/4

Qua: worst ratio <=2 / log....
1.3.11.7. O2 Cmax
Def: O2 Cmax

Algorithm: johnson

Qua: this is a feasible & optimal solution
Proof:
1)first prove that separatly they are feasible


2)then we combine those 2 and prove that they are still feasible

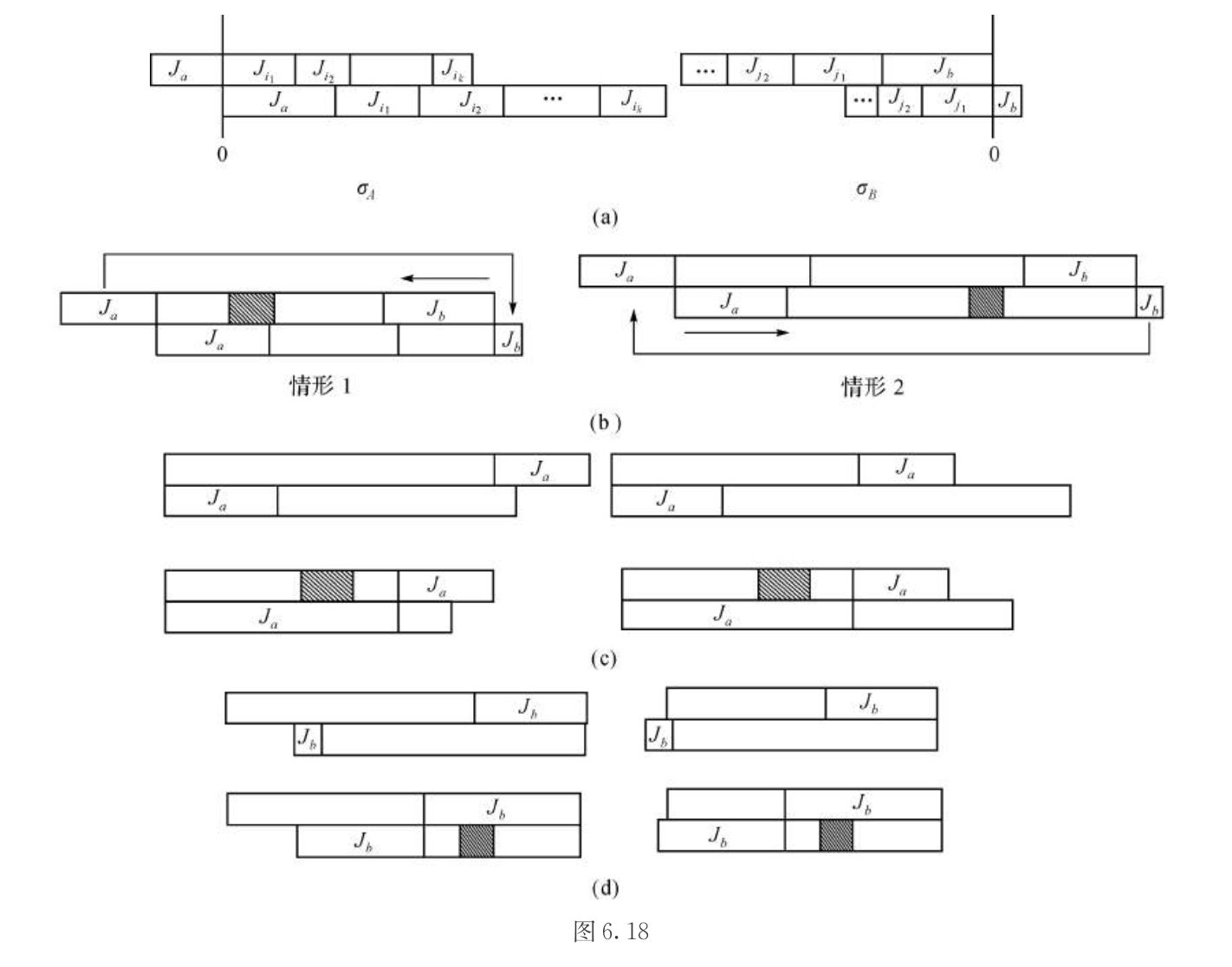
3)By equals lower bound(for min): prove optimal
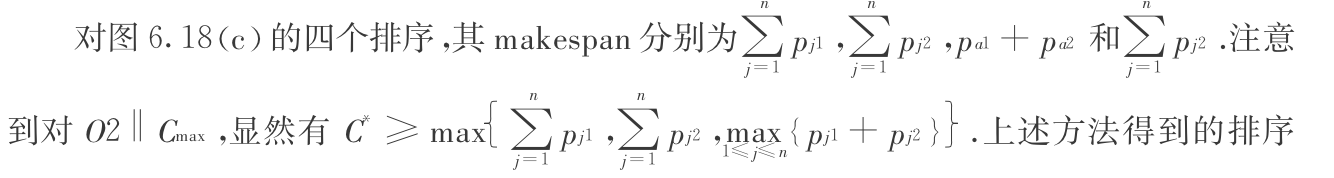
traverse through all possible solutions and get solution = lowerbound.
1.3.11.8. O3 Cmax
Def:
Qua:

1.3.11.9. Om Cmax
Def:
Qua: exist FPTAS

Qua: worst ratio

1.3.11.10. Jm Cmax
Def:
Qua: worst ratio >= ....

1.3.11.11. Rm Cmax(hw)
Def: ...
Qua: lb for some algo = m
Proof: \(\leq m\) => ...
\(\geq m\) => 1 and 1 + \(\epsilon\)
Qua: online lb
Proof: (1,1) => (1,2) & (2,1)
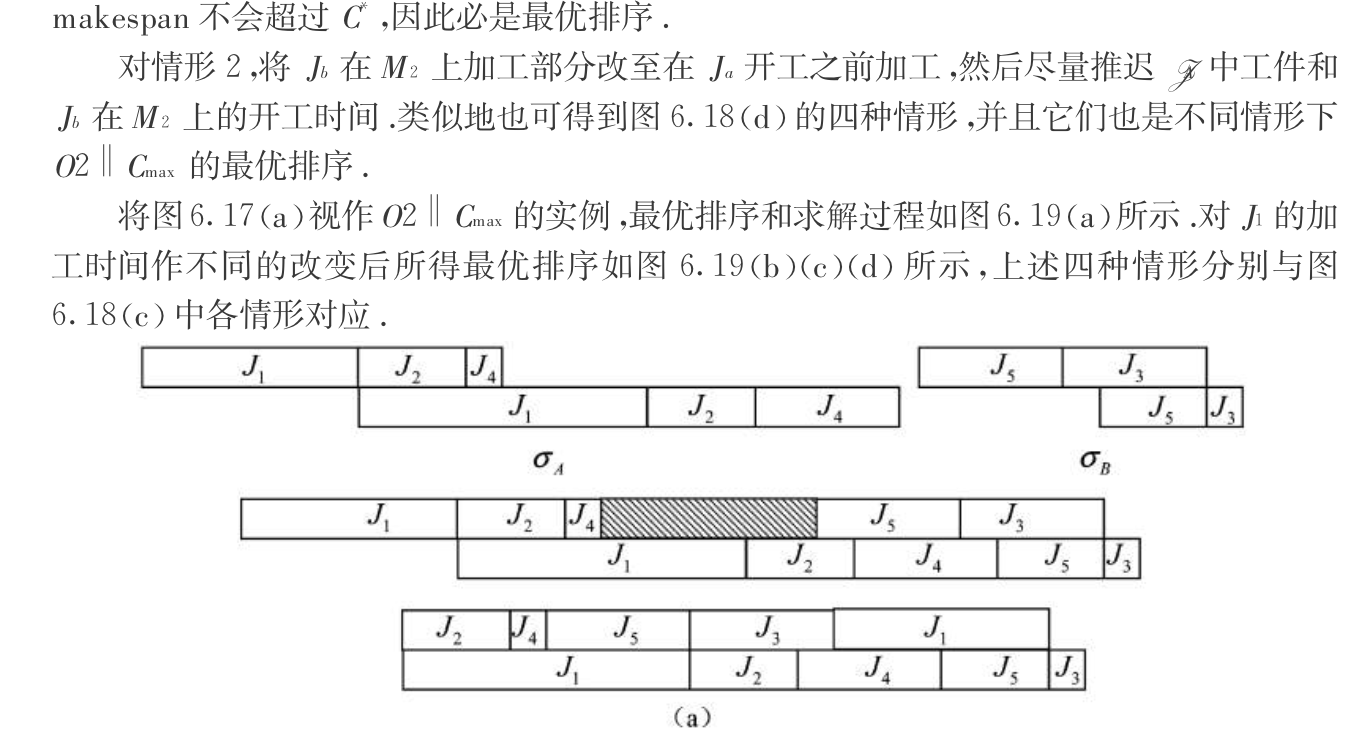
1.3.12. bin-packing
Def: bin-packing problem

Qua: worst ratio \(\geq\) 1.5

Proof: By gap tech, bin\(\leq p\) partition

1.3.12.1. next fit
Algorithm: next fit ( influenced by sequence )
Note: fit => fill; not fit => new box

Qua: worst ratio = 2
Proof:
1)By constrast, ratio \(\leq\) 2 ( from local => global )

2)ratio \(\geq\) 2, consider to let every box as empty as possible(at least C/2)
1.3.12.2. first fit
Algorithm: first fit
Note: 1 => j, fill the first fit or new bin


Qua: worst ratio = 1.7
Proof: proof is crazy, same idea: make boxes as empty as possible.

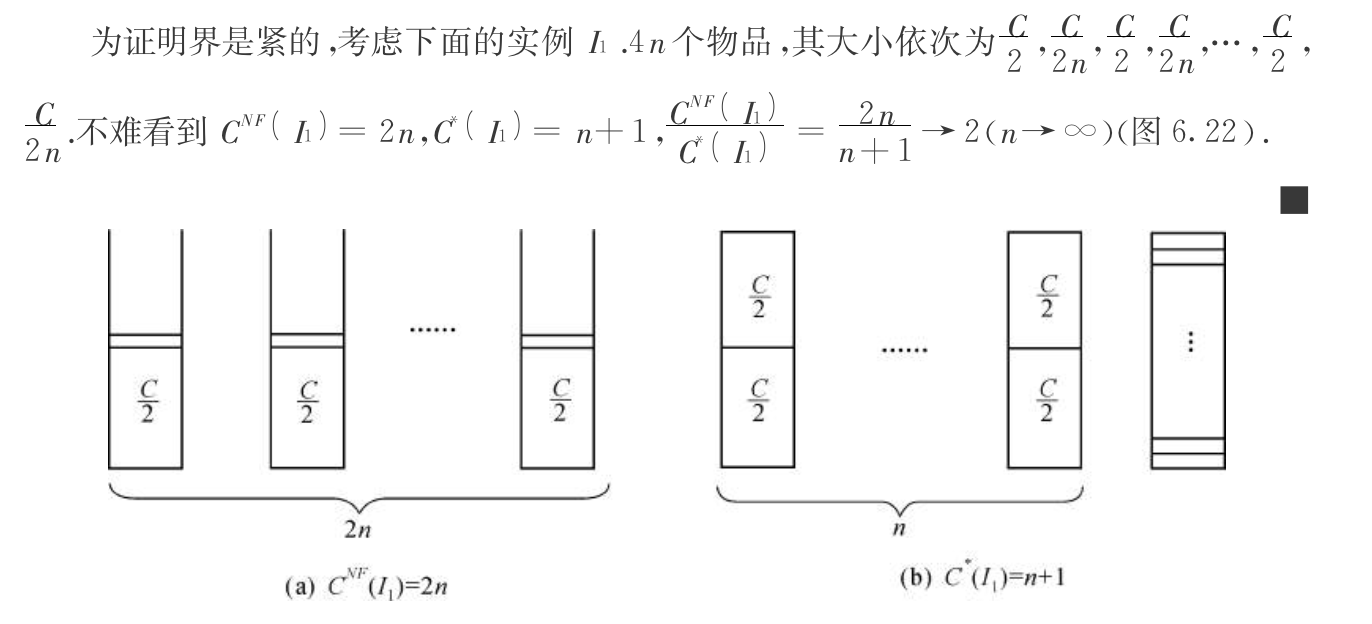
1.3.12.3. first fit decreasing
Algorithm: first fit decreasing (FFD)
Note: sort non-increasing + first fit, FFD provide sorting sequence which is very important.

Qua: worst ratio = 1.5
Proof: want to get upperbound for l => upperbound for pj and j
1)prove ratio \(\leq\) 1.5
1.1) By given FFD, prove upperbound for \(w_j\)

1.2) By given FF, prove upperbound for j

1.3) By, upperbound: finally prove it.
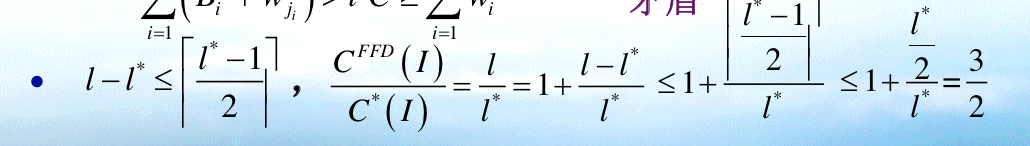
2)By l-l* lowerbound, which means trying hard to make them close: prove ratio \(\geq\) 1.5

Note: relaxation can be made => \(p_j \leq C/2\) will suffice ( see slides )
1.3.13. online ski-rental
Def: ski-rental problem

1.3.13.1. strat-N
Algorithm: strat-N

Qua: lb \(\leq\) 2

Qua: strat-N is the best of strat-K

Note: draw a diagram with ratio on instance level
1.3.14. bin-covering
Def: bin-covering problem

1.3.14.1. next fit
Algorithm: NF
Proof: By contraction.

Qua: ratio \(\geq\) 2

1.3.15. online searching
Def: online searching 1D
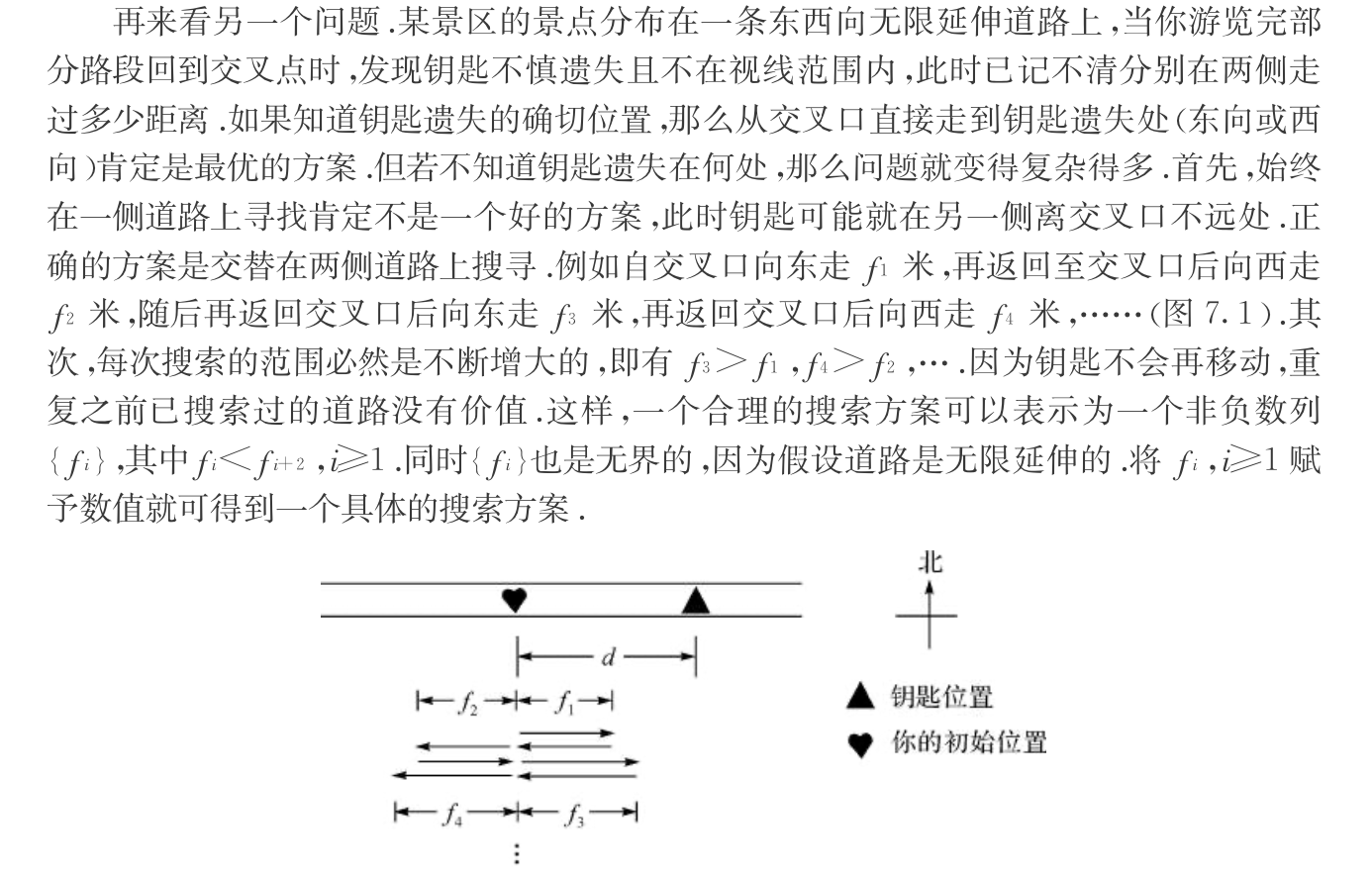
1.3.15.1. linear space
Algorithm: linear pace


Note: linear pace 2


1.3.15.2. exp space
Algorithm: exp pace

Qua: ratio \(\geq\) 9

Proof: By construction & contradiction

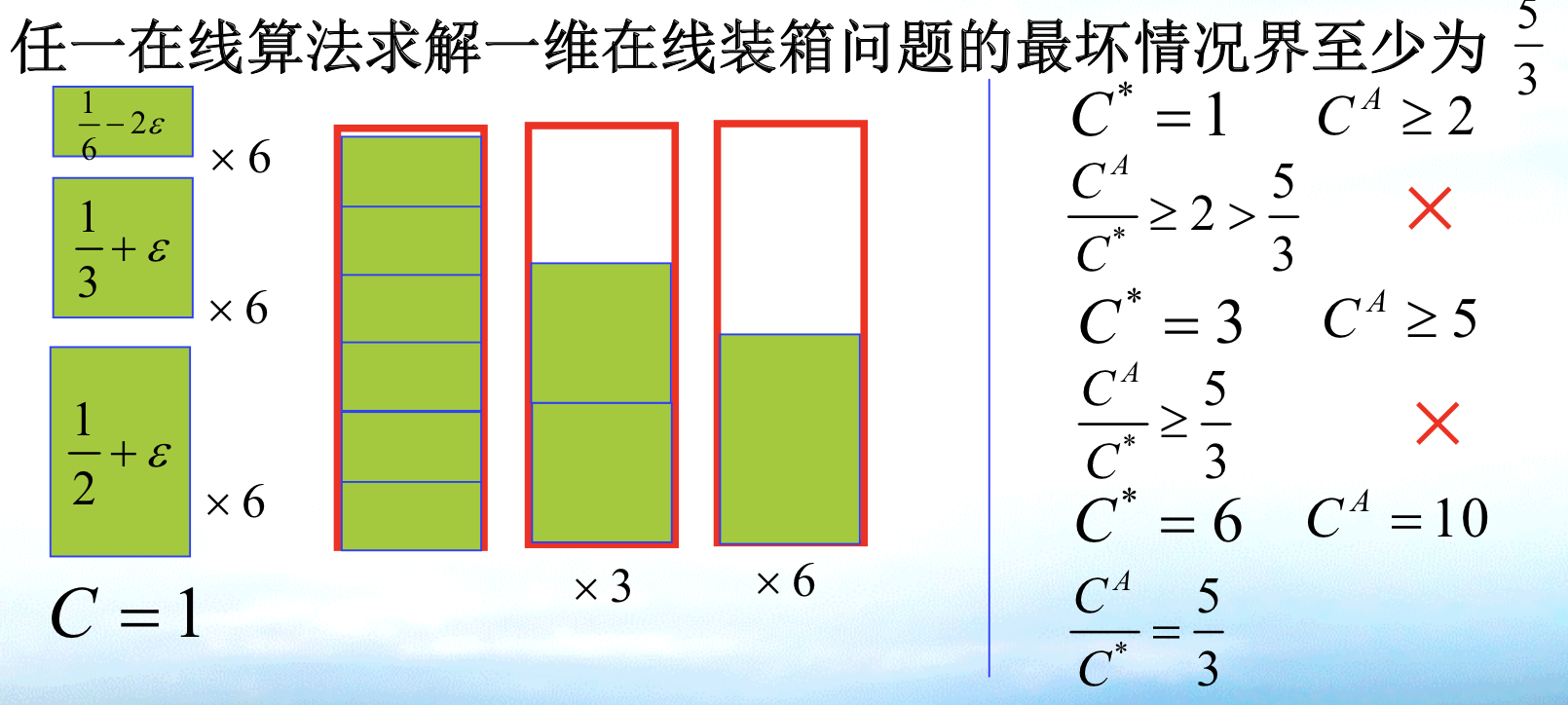
1.3.16. online bin-packing
Def:
Qua: ratio $$ 5/3
Note: note that we first give 6 1/6 -.., and it'll have to fit in 1. then give 6 1/3, it 'll have to fit in 4. then give 6 1/2, the optimal is 10, we get 5/3. 1)The whole process is about making local greedy optimal worse: 1/6 can be used in optimality but it is used to suffice local optimal. 2)The result is that we make ratio worse: First we get 1/1 => 4/3 => 10/6.
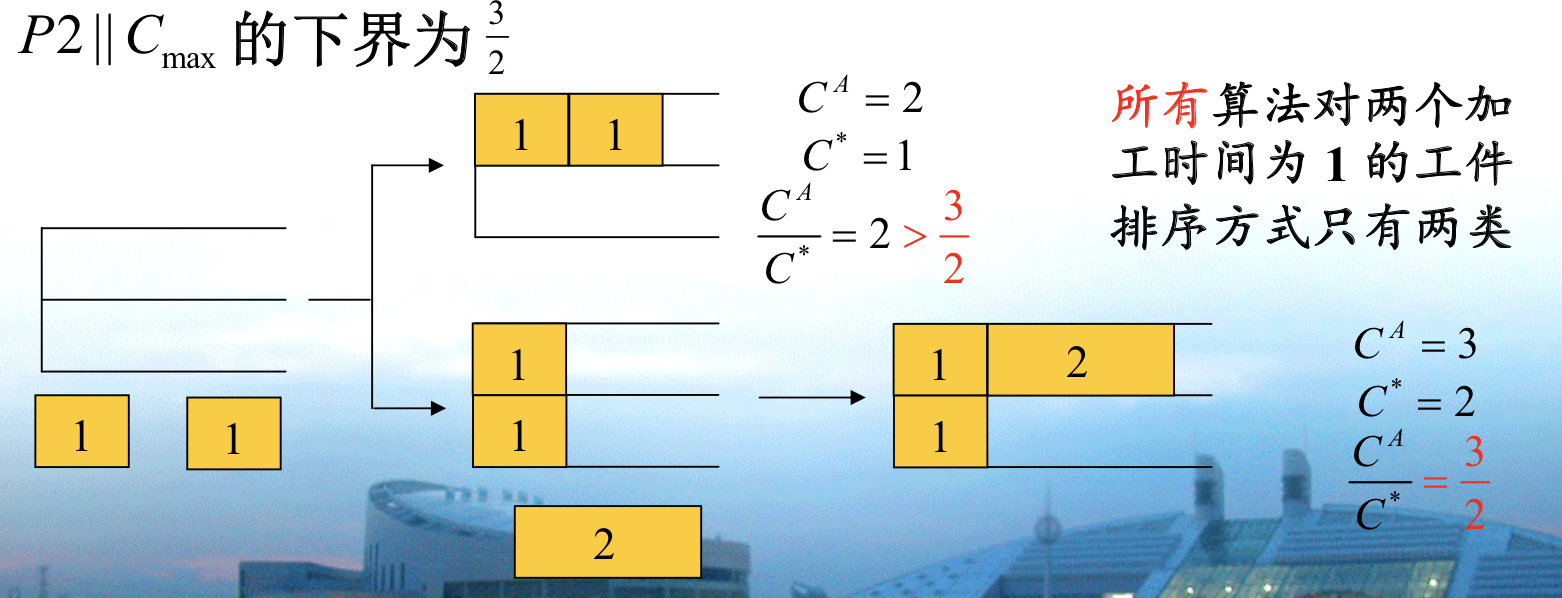
1.3.17. online scheduling
Def: P2||Cmax
Qua: ratio \(\geq\) 3/2
Note: the proof follows the same routine, since 1 can be used in 1 1 / 2, so we have to make it in local optimal solution and make it worse in global optimal solution.
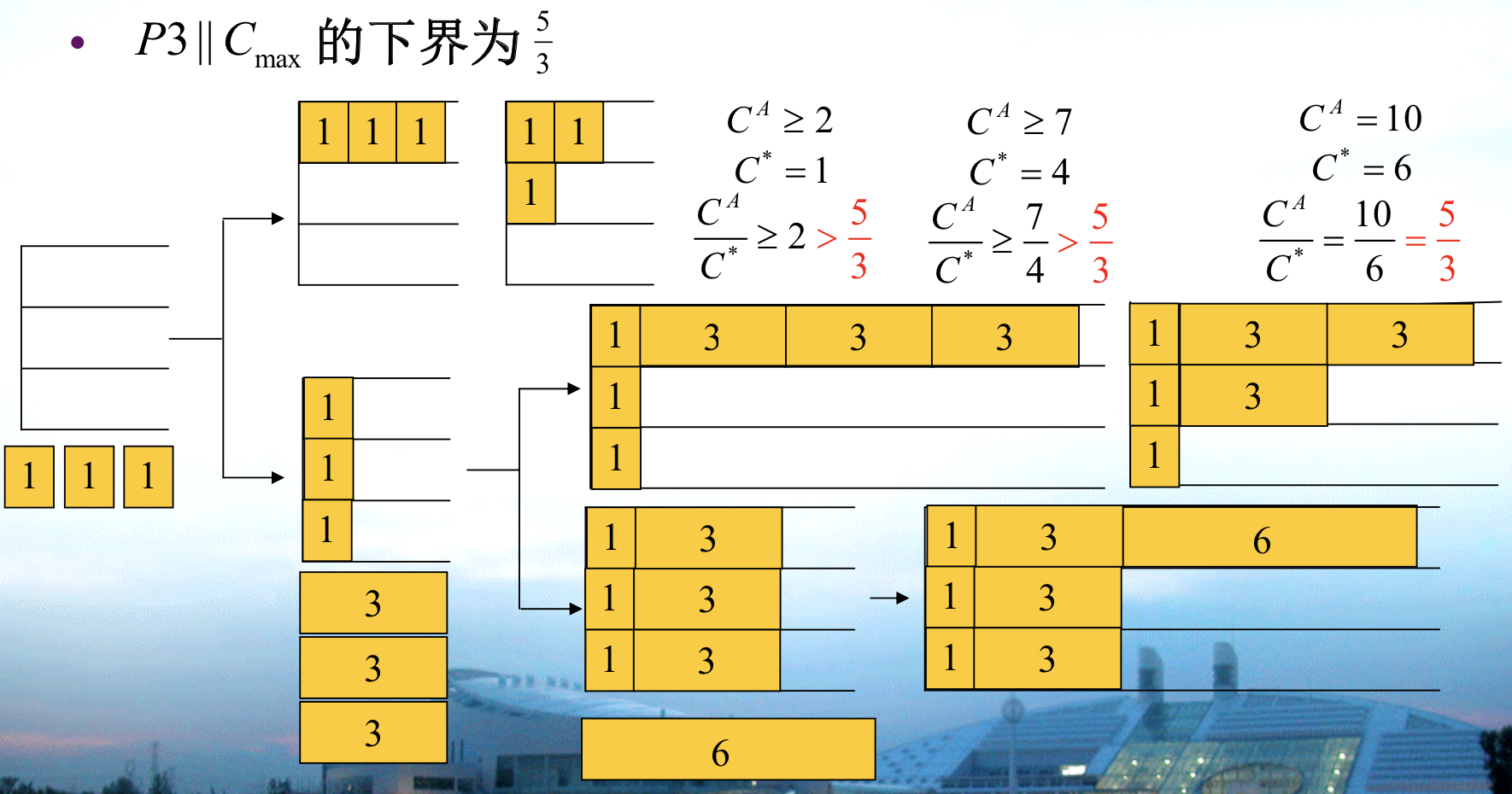
Def: P3 ||Cmax
Qua: ratio \(\geq\) 5/3
2. course homework
2.1. specific TSP problem
Def: tsp issue

2.1.1. 1) prove
Def: prove the following statment

- solution:
- y-x =1
- say born in {1,...X}, have to go at least one time back&forth to {X+1 ...n}
- y-x =2
- say born in {1...X}, can go to X+1-> {X+2...n} -> X, avoid 1 cost .
- y-x =1
- solution:
2.1.2. 2) prove TSP
Def: prove TSP

- solution:
- draw the symmetric matrix
- 画图题:
- 从对角线出发,y-x是距离对角线的距离,然后环游是两条y-x=1的对角线,画个图就ok。
- 而且该环游刚好是下届,证完。
- solution:
2.1.3. 3) prove
Def: prove

- solution:
- = min<= sum min =
- T(S) = constant
- solution:
2.2. specific sequencing problem
Def :

2.2.1. 1) prove \(\in\) NP
Def: prove

- solution:
- 从np定义出发,计算input size
- solution:
2.2.2. 2) prove
Def: prove

- solution:
- 从hamilton实例出发,构建作业:把顶点转为车子型号,无边则冲突,有边则不冲突
当hamilton有解,则车子顺序有解ux
当车子顺序有解,hamilton有解
- 从hamilton实例出发,构建作业:把顶点转为车子型号,无边则冲突,有边则不冲突
- solution:
2.2.3. 3) write in linear programming
Def: 改写为数学规划
- solution:
- xjt = 1 当第t辆车形为j
- solution:
- \(\sum_n xjt = nj j =1..k\)
- ${q=t}^{t+s_j} {i=1}^{k} x_{qi}a_{ij} r_j t=...,j=... $
## MAX-SAT
Def:

2.2.4. 1) write in linear programming
Def: write in linear programming

Solution:
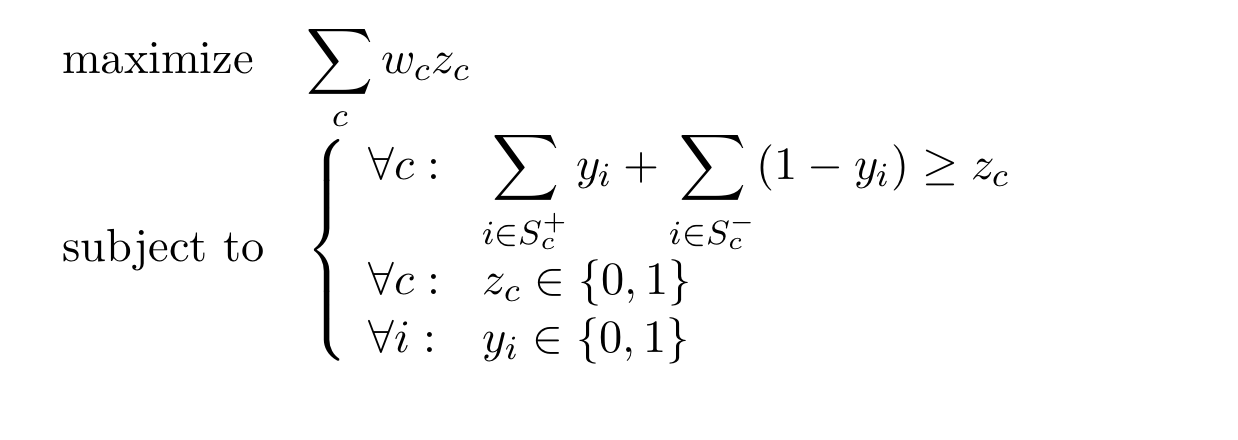
2.2.5. 2) write in
Def:

2.2.6. 3)
Def:

2.3. specific assign problem
- Def:
2.3.1. 1) write in integeral programming
Def: write in integeral programming
- Solution: \[ max P*X \\ s.t. x_{ij} =0/1 \\ \sum_{i,j=1}^{n} X _{ij}*j \leq T \]
Note: loss function have to be linear
2.3.2. 2) write in DP
Def: write in DP
- Solution: say DP[i][t] = maximum outcome for [i: end] with a budge of t . \[ \begin{equation} DP[i][t] = \left\{ \begin{array}{**lr**} max_j(DP[i-1][t-j]+p_{ij}) &j=1...t \\ p _{it}, & \text{if (i == n)} \\ \end{array} \right. \end{equation} \]
2.4. specific clique problem
- Def:
2.4.1. 1) prove trivial
2.4.2. 2) prove NP-hard
2.4.3. 3) give a algorithm of ratio = 2
Def: given a matching algorithm derive an algorithm for min vertex cover ratio = 2
Solution: add all max matching vertex \(M_v\) to result.
Proof: valid algorithm && ratio = 2
prove by contradiction that if matching vectexs do not necessarily cover all edges, it's not a max matching.
$= = 2 $
2.4.4. 4) prove trivial
- Def: prove ratio bounds, proof is trivial
2.5. specific subset sum
- Def: ...
2.5.1. 1) give an algorithm
- Def: trivial
2.5.2. 2) prove statement
Def: prove...
Solution: prove by contradiction
Note: 凑条件 \[ l(T_1)/l(T_2) > a + l(T_3)/l(T_1) > a => \\ l(T_3)/l(T_2) > a^2 => \\ S_k > (a^2 -1 )S_{k+1} \geq (a^3-a)S_k =>contradiction \]
2.5.3. 3) give an \(\alpha\)- algorithm
Def: ...
Solution:
if a => select Sk and Sk+1
if b => use 2.6.1
if !(a || b) => use 2.6.2, since \(C^* \geq 1\) and we can always find \(C_A \leq a\) , so worst ratio \(\leq a\)
2.6. p2 || Cmax
Def: ...
IMG_0485 Note: special case for p2 || cmax where c* = C
Qua: lb \(\geq\) 4/3
Proof: note that c* = C so only "final shot" matters.
since we want to prove 4/3, give intuition for 1/3
1/3 + 1/3 + 2/3 + 2/3 / 1/3 + 1/3 + 1/3 1
Algorithm: give an algorithm of 4/3
Proof: 4/3 * 2 > 2
## specific backpacking
Def:

### 1)
- Def:
- Solution: ez
2.6.1. 2)
Def:

- Solution: ez
2.6.2. 3)
Def:
- Solution: ez
2.6.3. 4)
Def:
- Solution: ez
3. exam
3.1. 概念
3.1.1. 问题
3.1.1.1. 时间复杂度
3.1.1.2. 复杂类
3.1.1.3. 实例
3.1.1.3.1. 规模
3.1.1.3.2. 最大数
3.1.1.4. 近似
3.1.1.4.1. 在线问题...
3.1.2. 算法
3.1.2.1. 近似
3.2. 问题
3.2.1. 背包
3.2.2. tsp
3.2.3. sat
3.2.4. 排序
3.2.5. 划分
3.2.6. 装箱
3.2.7. 子集合
3.2.8. 定点覆盖
3.2.9. 匹配
3.2.10. 在线。。
3.3. 算法
3.4. 方法
npc证明方法=>规约/子问题
多项式时间算法
最优算法=>规划,动态规划,分枝丁界
近似算法=>贪婪

