Probability Theory Notes
1. frequency & probability
1.1. probability space
1.1.1. Kolmogorov’s probability model
Def1.7: probability space (\(\Omega\), \(\mathscr{F}\), P) ,
Usage: is a special kind of measure space, see for more details. https://blog.csdn.net/tankloverainbow/article/details/102872112
Example: finite sample spaces

Example: infinite sample space


Def1.8: \(P=F ( \mathscr{F} -> R )\), is a finitely additive set function, a measure.
Qua1.9: => Non zero
Qua2.0: => P(must) =1
Qua2.1: => linear
s.t AB does not overlap:
P(A+B) =P(A)+P(B)
1.1.2. special probability spaces
1.1.2.1. frequency norm
Def1.1: frequency of A (A is a 0-1 variable), frequency is a way to depict clasiical probability \[ F _{N}(X) = \frac{n}{N} \]
- Qua1.2: => non-negative:
\[ F _{N}(X) \geq 0 \]
Qua1.3: => regularity:
s.t. X must happen
Qua1.4: => addable:
s.t. A B doesnot happen at once ( A B does not equal 1 at once)
\[ F _{N}(A+B) = F _{N}(A) + F _{N}(B) \]
1.1.2.2. classic norm
Def1.5: classic norm is a special probability space
We set eventspace to be finite, then we define P: where P(event) is \(1/|eventspace|\) regardless of their differences.
1.1.2.3. geometry norm
Def1.6: geometry norm is a special probability space
We set eventspace to be infinite, the rest is same as classic norm.
1.1.2.4. n-Bernoulli norm
Def1.7: is a special probability space
sample = {w1~n} (n bernoulli 0/1)
samplespace = {\(2 ^{n}个sample\)}
P({X=k}) = \(C(n,k)p^k(1-p)^{n-k}\)
1.2. conditional probability
1.2.1. conditional prob
Def1.7: conditional prob
s.t $P(B) 0 $ \[ P(A|B) = \frac{P(AB)}{P(B)} \]
1.2.2. all prob equation & bayes equation
Def1.8: complete event group \(\left\{ A1, A2,...An \right\}\) \[ (1) Ai \; not \; overlap \\ (2) P(Ai) >0 \\ (3) \sum_{n = 1}^{\infty}Ai = ALL \]
Theorm1.8: all prob equation
s.t. \(\left\{ A1, A2,...An \right\}\) is complete event group \[ P(B) = \sum_{n = 1}^{\infty}P(A_i)P(B|A_i) \]
Theorm1.9: bayes equation
s.t. \(\left\{ A1, A2,...An \right\}\) is complete event group \[ P(A_i|B) = \frac{P(A_i).P(B|A_i)}{\sum_{k = 1}^{\infty}P(A_k).P(B|A_k)} \]
Def1.10: priori prob \[ P(A_i) \]
Def1.11: posteriori prob \[ P(A_i|B) \]
1.2.3. independence (of event)
Def1.12: dependence of collection of event

Def: dependence of collection of event

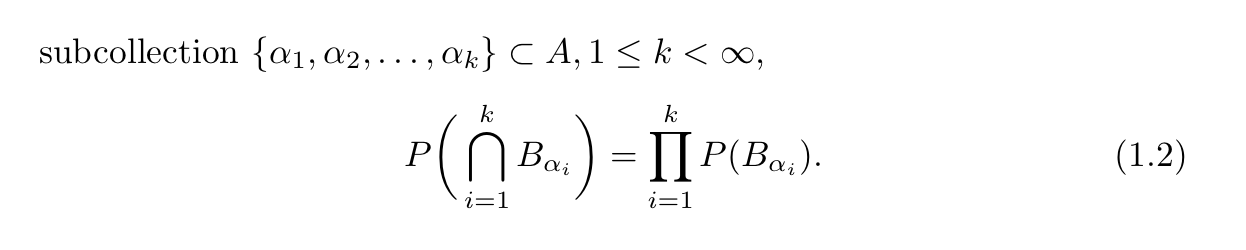
Def: dependence of collection of event

1.3. L2 space
Def:l2 space
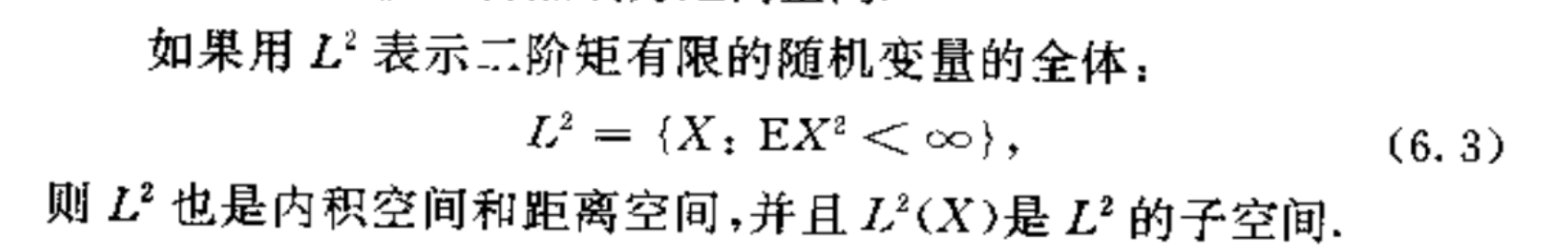
Qua: => hilbert

Proof:

2. random variables
2.1. distributions
Def: random variable X is a measurable function, F(samplespace to R)
Usage: distributions are determined by 2 factors: X and P, since we do not know P, so we do not accutually care if random variable is defined on the same Probabilty space or not, they can be or they can not.
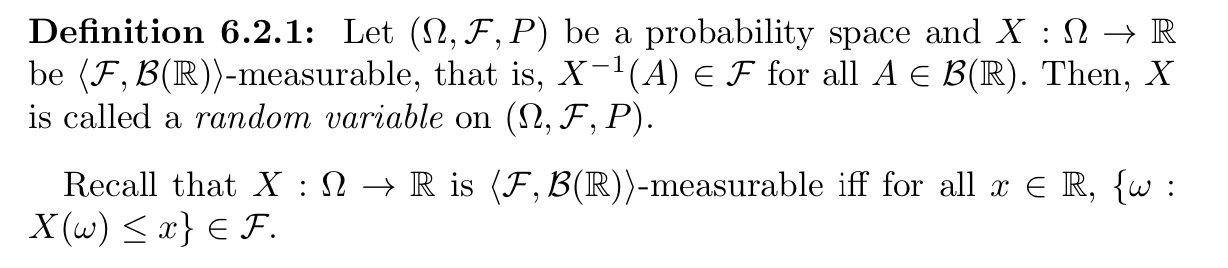
Def: discrete / continuous random variables
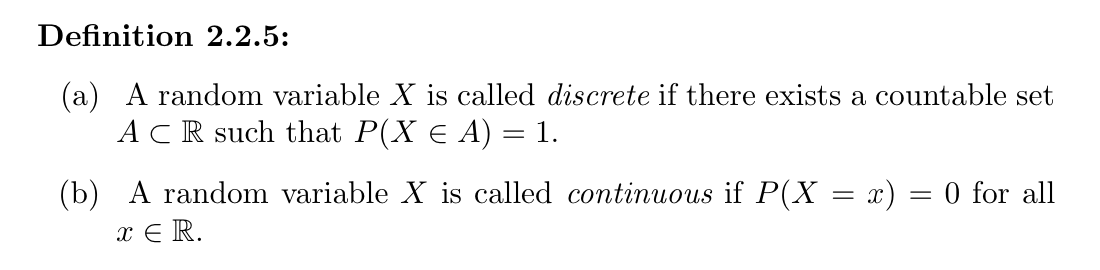
Note: other definitions
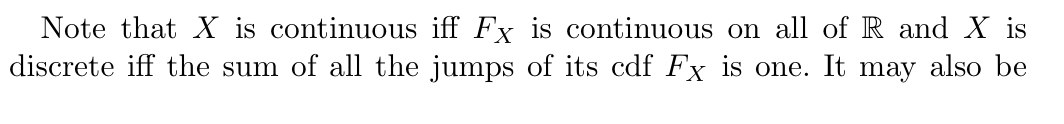
Note: decomposition of F(x) if X is neither continuous nor discrete

2.1.1. pdf
Def: Probability Distribution of X(w)
Usage: a induced measure from R to $ $


Def2.6: Probability Density Function of X(w) \[ p _{X}(k) = F _{X}'(k) \]
Qua2.7: => single point $$ \[\begin{align} P(X=k) &= F(k)-F(k-0) \\ &= \lim_{h \to 0+} \int_{k-h}^{k}p(y)dy \\ \end{align}\] $$
Qua2.8: => non-negative \[ p _{X}(k) \geq 0 \]
Qua2.9: => regularity \[ \int_{n = - \infty}^{\infty}p_{X}(y)dy =1 \]
2.1.2. cdf
Def2.2: Cumulative Distribution Function of X(w) (cdf)
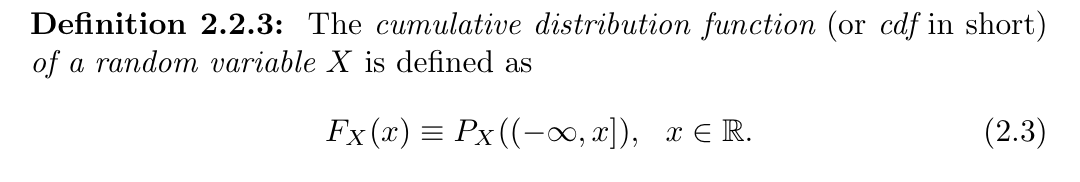
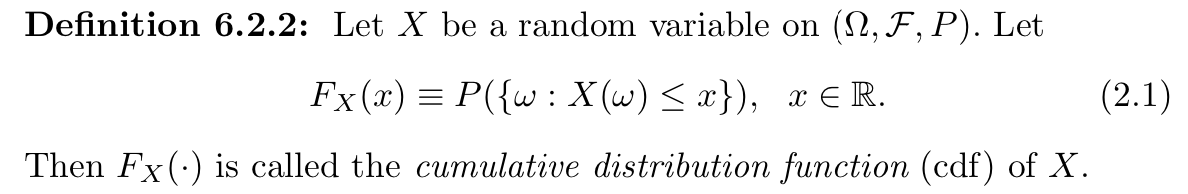 \[
F _{X} (k) = P(X \leq k) = \int_{- \infty}^{k}p_{X} (y)dy
\]
\[
F _{X} (k) = P(X \leq k) = \int_{- \infty}^{k}p_{X} (y)dy
\]Qua: necc & suff
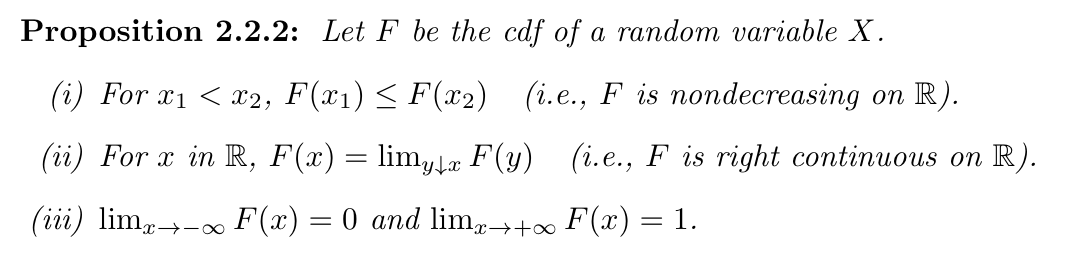
2.2. special functions
2.2.1. expectation
Def1.1: expectation of random variable

s.t. (1) \[\sum_{k}^{} |k|*P_(X=k) < \infty\] \[ Func(X)=E(X)=\sum_{k}^{} k*P_(X=k) \\ Func(X)=E(X)=\int_{k} k*p_X(k) dk \\ Func(X)=E(X) =\int_{\Omega}X(w)dP(w) \]
Qua1.2: some useful expectations

Qua1.3: => monotonicity
s.t. $ a X b $ \[ (1) E(X) \exists \\ (2) a \leq E(X) \leq b \]
Qua: => monotonicity
s.t. (1) \(|X| \leq Y\)
(2) $E(Y) $
\[ E(|X|) \exists \]
Qua1.4: => linearity (E into sumation)
s.t.$Ex1, Ex2...Exn $ \[ E( \sum_{n = 1}^{\infty}ciXi+b) =ci \sum_{n = 1}^{\infty}E(Xi)+b \]
Qua1.6: => limitation (bound and convergence)
s.t. (1) \(\lim_{n \to \infty}X _{n}(w)=X(w)\)
(2) for all \(n \geq 1\), \(|X _{ n}| \leq M\) \[ \lim_{n \to \infty}E(X _{n}) = E(X) \]
Qua1.11: operation
s.t. (1) g(x) is borel function
\[ Eg(X) = \int_{- \infty}^{\infty} g(k)p_X(k)dk \]
Qua1.12: => steins theroy
s.t. (1) X~N(0,1)
(2) g is continuous & derivable
(3) \(E|g(X)X|< \infty\)
(4)\(E|g'(X)|< \infty\) \[ E|g(X)X|=Eg'(X) \]
2.2.2. variance
Def: Bias ( is a metric of approximation X to a ) \[ Bias( \hat{X},a )= E( \hat{X})- a=number(\hat{X}) \]
Def: MSE ( is a metrics of approximation) \[ MSE(\hat{X} ) =E(\hat{ X} - a) ^{2} = V(\hat{X})+Bias^{2}(\hat{X},X ) =number(\hat{X}) \]
Def: length \[ Length(\hat{X}) = E||\hat{X}||^2 \overset{when E(\hat{X})=a}{=} MSE(\hat{X})+||a||^2=number(\hat{X}) \]
Def1.13: deviation \[ D(X) = X-E(X)=randonvariable(X) \]
Def1.14: variance
s.t. abs < inf
\[ V(X) = E(D(X)^{2})=E(X-E(X)) ^{2}= E||X||^2-E(X)^TE(X)=number(X) \]
- Qua1.16: => var = 0 means degenerate
- Qua1.17: => quadratic
\[ V(cX+b) = c ^{2}V(X) \]
Qua1.18: => sup
s.t. \(c \ne E(X)\) \[ V(X) < E(X-c)^{2} \]
Qua1.19: => double linearity
\[ V( \sum_{n = 1}^{\infty}Xi)= \sum_{n = 1}^{\infty}V(Xi)+2\sum_{1 \leq i<j \leq n}^{}E(Xi-EXi)E(Xj-E(Xj)) \]
2.2.3. moment
Def2.27: moment, 原点/中心 \[ m_k = EX ^{k}\\ c_k = E(X-EX) ^{k} \]
Qua2.27: => relationship between different moments

Qua2.27: => equatiom

Qua2.27: => moment & cmf

2.2.4. characteristic function
Def2.28: cf
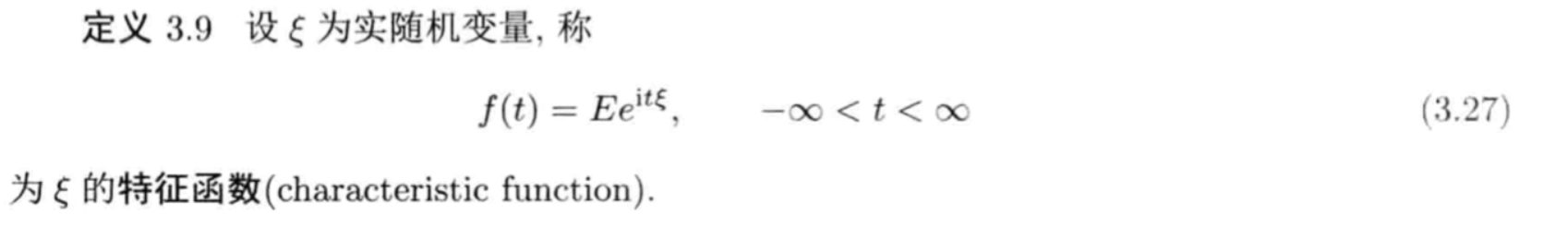
Qua2.29: => 1 on 1

Proof
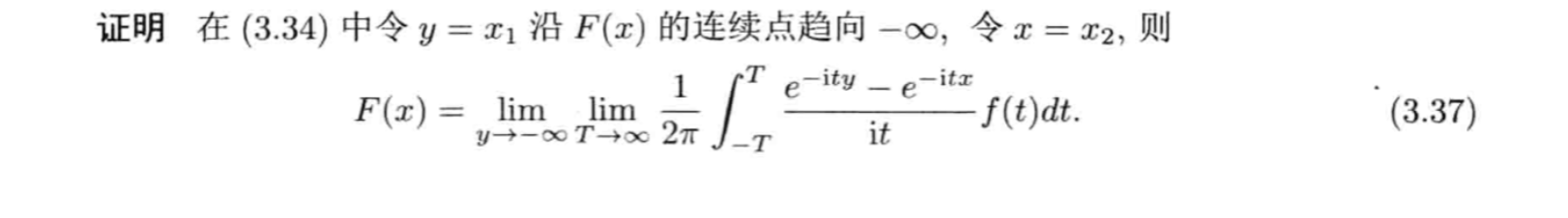
Qua2.30: => 0 is the largest
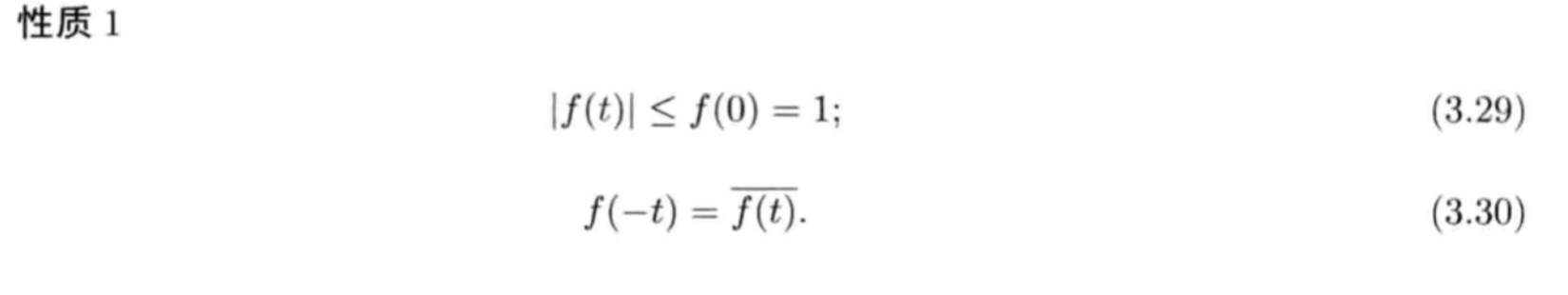
Proof:
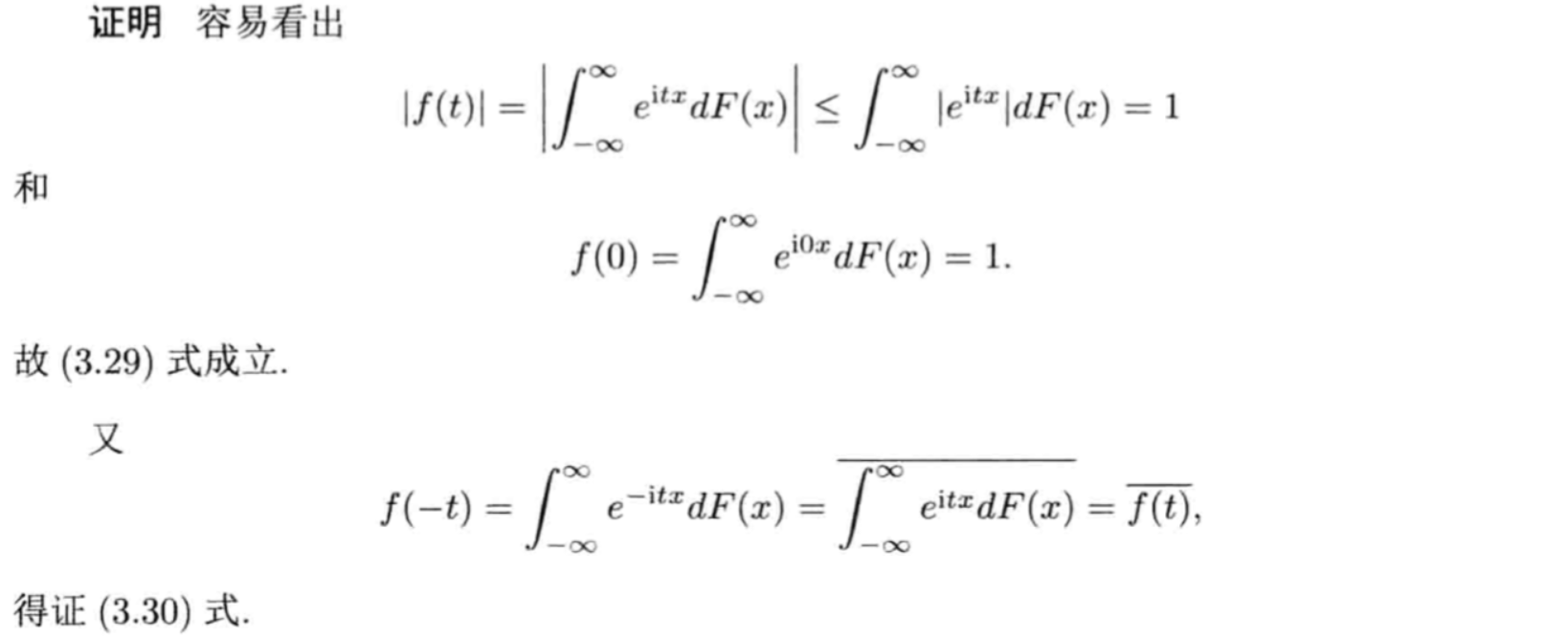
Qua2.31: => 一致continuous \[ f(t) \to -\infty\ , \infty)一致 continuous \] Proof: too long
Qua2.32: => 非负定

Proof:

Theorm2.33: Bochner-K, necessary and sufficient condition;

Qua2.34: => Cf & moment

Proof: too long
Qua2.35: => linearity
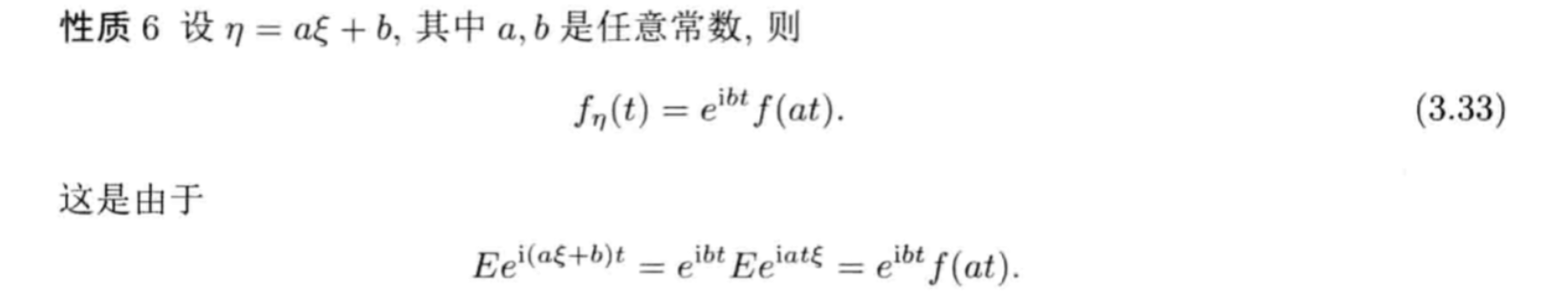
Qua2.36: => cf & cmf

Proof:
Qua2.37: => cf & cmf

2.2.5. generating function
Def2.38: generating function

Qua2.39~2.42: =>

Qua2.43: => gf & cf

2.2.6. martingale
Def:

Qua: =>

3. relationships of random variables
3.1. conditional & joint
3.1.1. joint distribution
Def: joint cdf
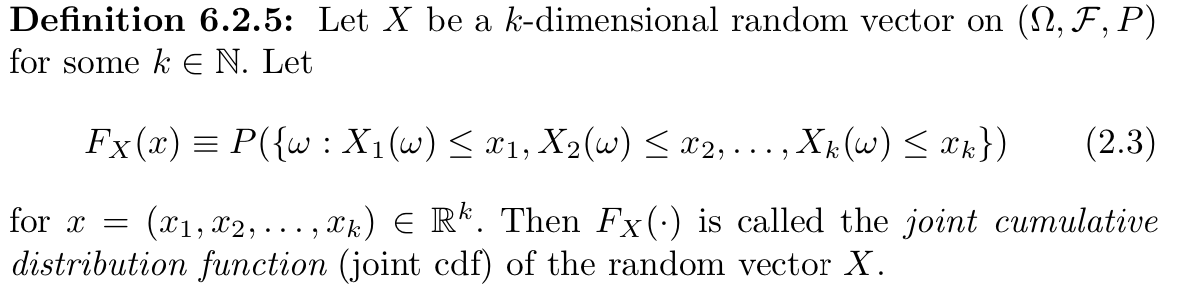
Def: joint pdf

3.1.2. conditional distribution
Def: conditional cumulative function \[ F _{X|Y}(c|b)=P(X \leq c|Y=b) = \sum_{x_i \leq c}^{}p _{X|Y}(x_i|b)=number(c,b,X,Y) \\ F _{X|Y}(c|b)==P(X \leq c|Y=b) = \int_{- \infty}^{c} \frac{p_{X,Y}(v,b)}{p _{Y}(b)}dv=number(c,b,X,Y) \]
Def: conditional density function \[ P _{X|Y}(c|b) = \frac{P(X=c, Y=b)}{P(Y=b)}=number(c,b,X,Y) \\ P _{X|Y}(c|b) = \frac{p_{X,Y}(c,b)}{p _{Y}(b)} =number(c,b,X,Y) \]
Def conditional probability of a event A given random variable X \[ not important \]
3.1.3. conditional expectation (projection)
3.1.3.1. conditional expectation
Def: conditional expectation of Y given X
 Note: other definition
Note: other definition
Note: other definition: also called projection

Example:
case of discrete random variable
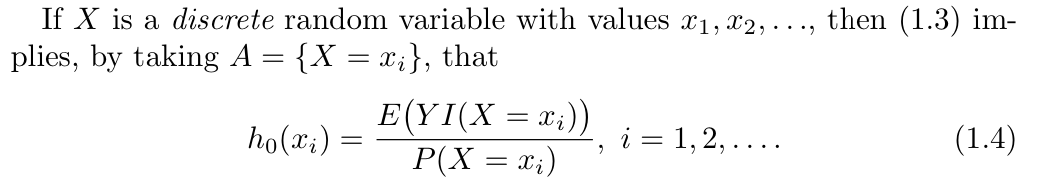
case of continuous random variable
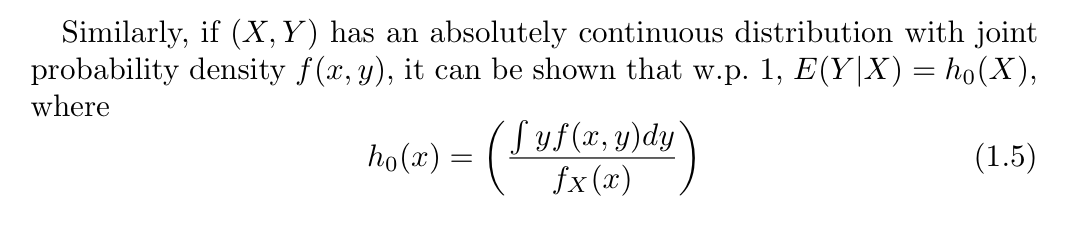
Qua: => basic quality

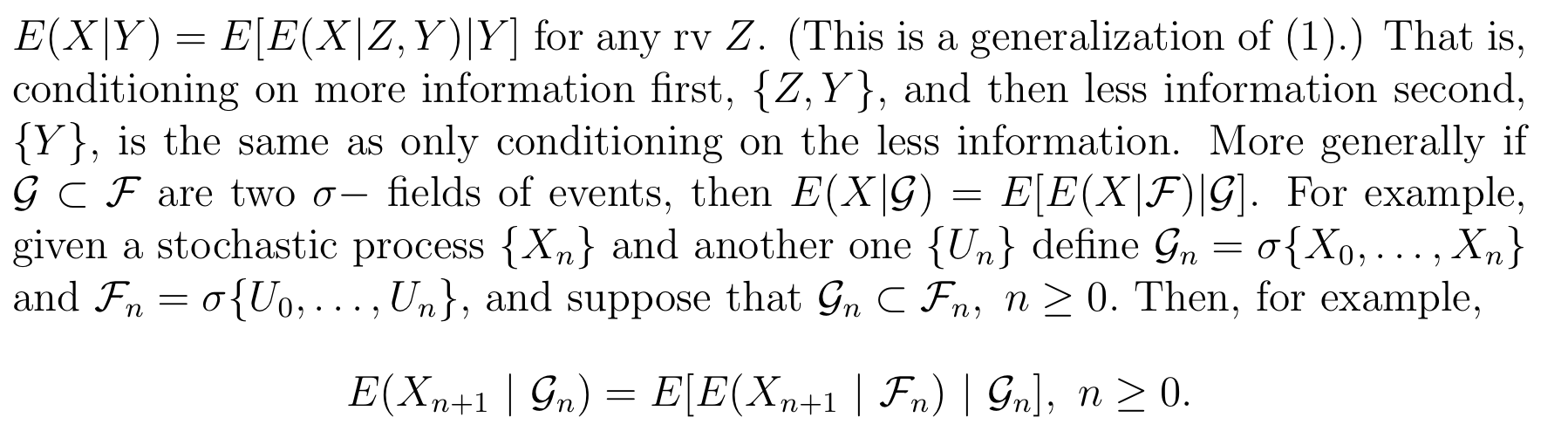


Qua: => some equality (2-4)

Theorem: => existence
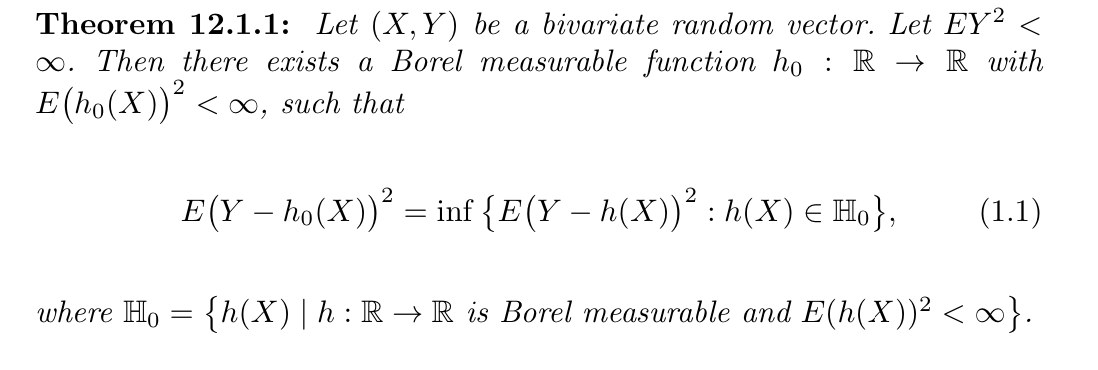
Theorem: (2-4) => equation

Theorem: (2-4) => equation

Lemma: ? (2-4) => equation

3.1.3.2. conditional expectation of Y given \(\mathscr{G}\)
Def: conditional expectation of Y given \(\mathscr{G}\)
Usage: a more general situation

Note: other definition


Qua: => existence

Qua: => some qualities
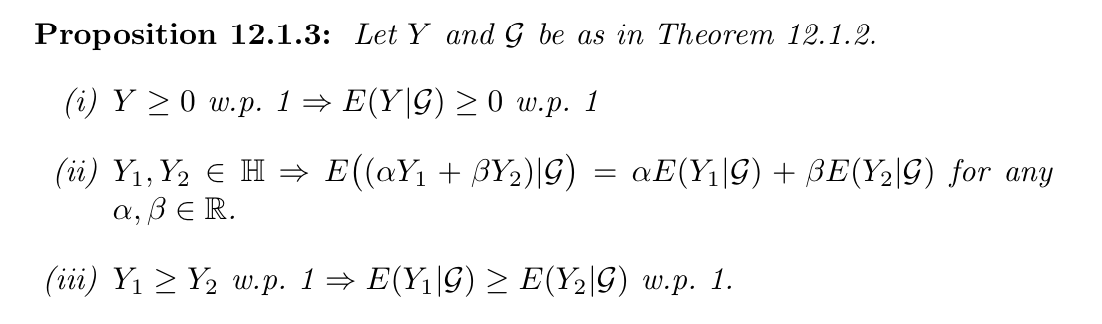
Qua: => some more qualities (all expectation equation)

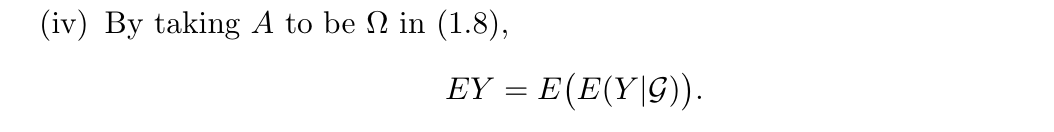
Qua: => the more general version of computation

3.2. special functions
3.2.1. covariance
Def1.20: co-variance
s.t. abs < inf \[ Cov(X,Y)=E _{X,Y}(X-E(X))(Y-E(Y)) = number(X,Y) \]
- Qua1.21: => \(Cov(X,Y) = EXY -EXEY\)
- Qua1.22: => \(Cov(aX,bY)=abConv(X,Y)\)
- Qua1.23: => \(Cov( \sum_{n = 1}^{\infty}Xi,Y)= \sum_{n = 1}^{\infty}Cov(Xi,Y)\)
3.2.2. correlation coefficient
Def2.24: correlation coefficient
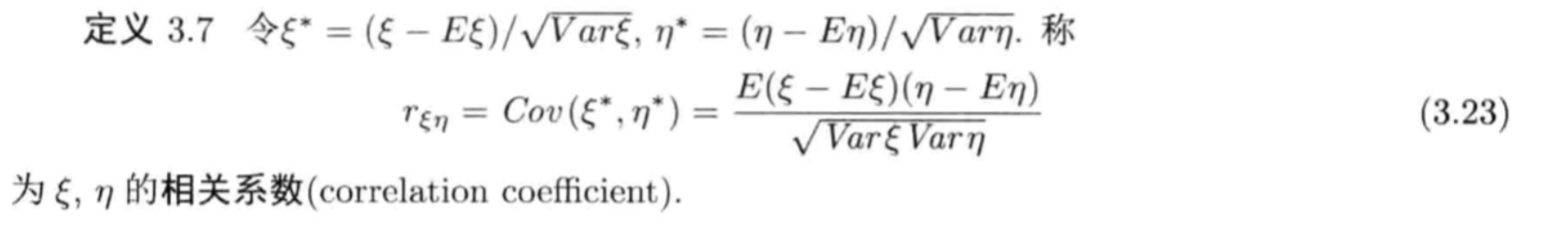
Qua2.25: => when r = 1 or -1
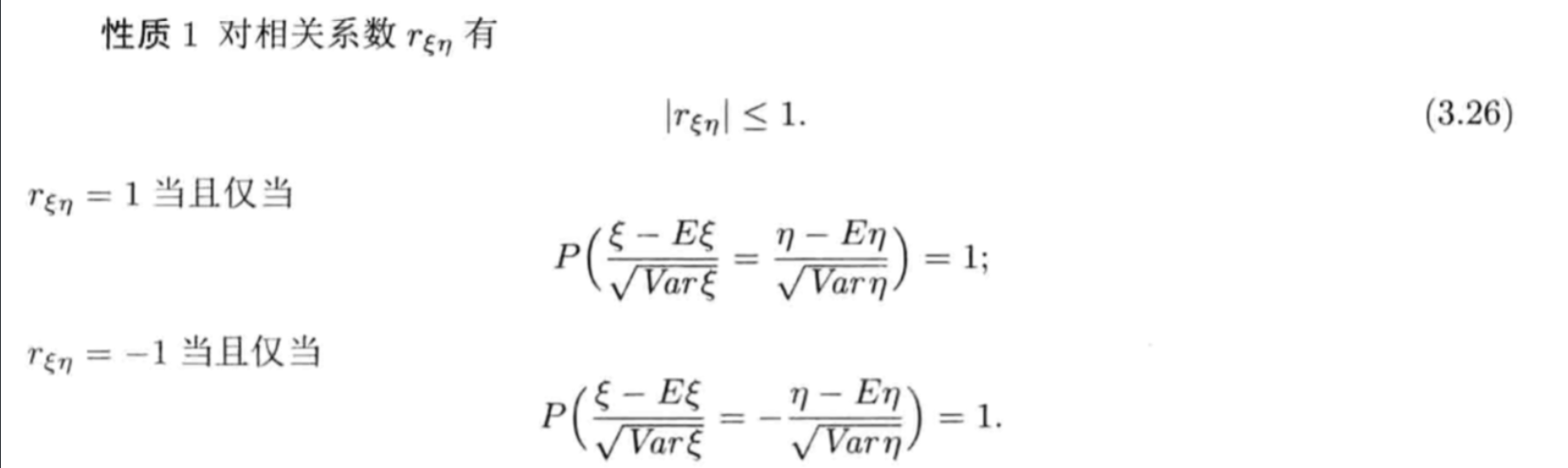
Proof:

Qua2.26: => relationship with E & Cov

3.2.3. conditional expectation
Def1.7: conditional expectation
$$ \begin{aligned} & E(X|H) = = _{x }x \ & E(X|H) =
\end{aligned} $$
\[ \begin{aligned} &E(X|Y=k)= \sum_{v}^{} v*p _{X|Y}(v|k)=number(k,X,Y) \\ & E(X|Y=k)= \int_{- \infty}^{\infty} v*p _{X|Y}(v|k)dv =number(k,X,Y)\\ & E(X|Y) = randomvariable(Y) \end{aligned} \]

Example:

Qua1.8: => total expectation fomula \[ E(E(X|Y)) = E(X)\\E _{Y}(E(X|Y)) = \sum_{k}^{}E(X|Y=k)P(Y=k)= E(X) \]
Qua1.9: => take out the known \[ E (g(X)Y|X)=g(X)E (Y|X) \]
Qua1.10: => Caughty \[ |E(XY|Z)| \leq \sqrt{E(X ^{2}|Z)} \sqrt{E(Y ^{2}|Z)} \\ |EXY|^{2} \leq E X ^{2} EY ^{2} \] Proof:

3.2.4. KL divergence (2-9)
Def: a group of function
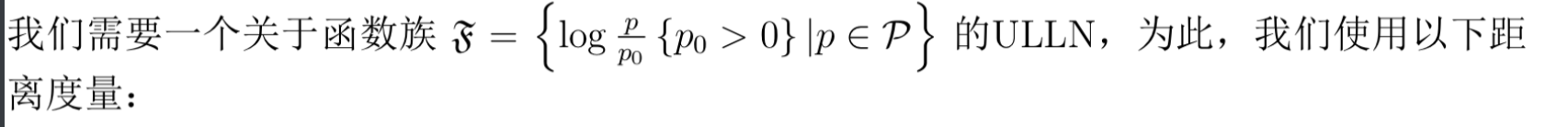
Def:

Qua: accutually not a formal distance, but can be used to metric the distance between distributions.
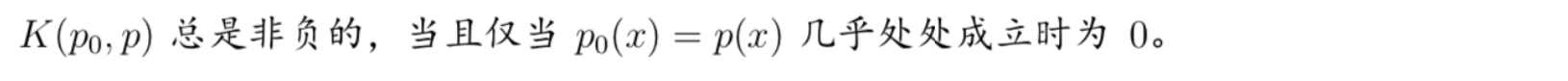
3.2.5. Hellinger distance (2-9)
Def: a group of function

- Def: Hellinger distance

- Qua: => KL distance
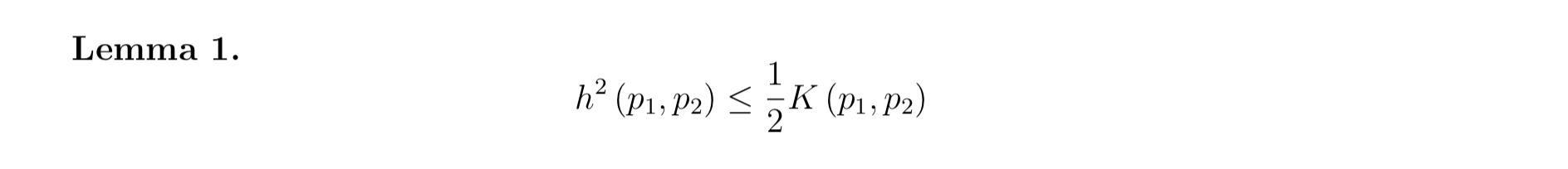
proof:

Qua: => upper bound
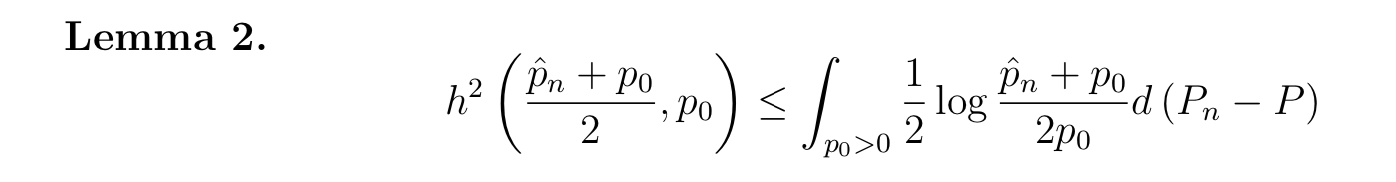
proof:
 acctually from MLE definition and KL and He relationship
acctually from MLE definition and KL and He relationship
Theorm: relation ship between above two group of function

- example:

t this distribution satisfy the Theorm, thus the empirical is very useful.

3.3. indepence & correlation
3.3.1. indepence
Def3.1: independence of random variable

\[ F_{XY} () =F _{X }()F _{Y}() \\p _{XY} = p _{X} p _{Y} \]
Qua3.1: Gaussian => ind
s.t. X1, X2 is variable gaussian \[ X1,X2 \text{ is uncorrelated = X1,X2 is independent} \]
Qua3.2: ind => E
s.t. X1, X2 independence \[ E(X1X2) = E(X1)E(X2) \]
Qua3.3: ind => uncorrelation
s.t. (1)X1, X2 independence
(2)X1 X2 var not inf \[ X1,X2 \text{ is uncorrelated} \]
Qua3.5: ind => character function

Qua3.6: ind => conditional expectation
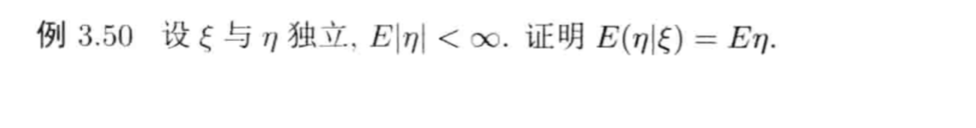
Proof:
3.3.2. correlation
- Def3.2: correlated \[ r _{XY} = \pm 1 \Rightarrow XY\text{ is probability 1 linear} \\ r _{XY} = 0 \Rightarrow XY \text{ is uncorrelated} \]
3.4. transformation
Theorm2.: transformation of continuous to continuous
s.t. (1) \(g(x)\) strictly mono
(2) \(g ^{-1}(y)\) has continuous derivation \[ (1) Y=g(X) \text{ is continuous random variable}\\ (2) g _{Y}(k) = \begin{cases} p(f ^{-1}(y))|f ^{-1}(y)'| & k \in f(x)值域\\ 0& otherwise \end{cases} \]
Theorm2.: transformation of continuous to continuous +
s.t. (1) \(g(x)\) strictly mono in non-overlap areas. And areas add up to \(\infty\)
(2) $ g ^{-1}(y)$ has continuous derivation in non-overlap areas. \[ same \]
Therom: transformation of continuous vector(x1,x2..xn is continuous) to continuous \[ (1) Y=f(x1,x2,...,xn)\\ (2)F _{Y}(k) = \int \limits_{Y \leq k}p_{X1...Xn}(x1,...xn)dx1...dxn \]
Theorm: transformation of continuous vector(x1,x2..xn is continuous) to continuos vector
s.t. (1) m = n
(2) ... \[ ... \]
Theorm2.1x**: convolution equation \[ P(X+Y=c) = \sum_{k = 0}^{r}P(X=k)P(Y=c-k)\\ P_{X+Y}(c) = \int_{- \infty}^{\infty}p _{X}(k)p _{Y}(c-k)dk \\ \]
3.5. classic bounds
3.5.1. jensen inequality
Def:
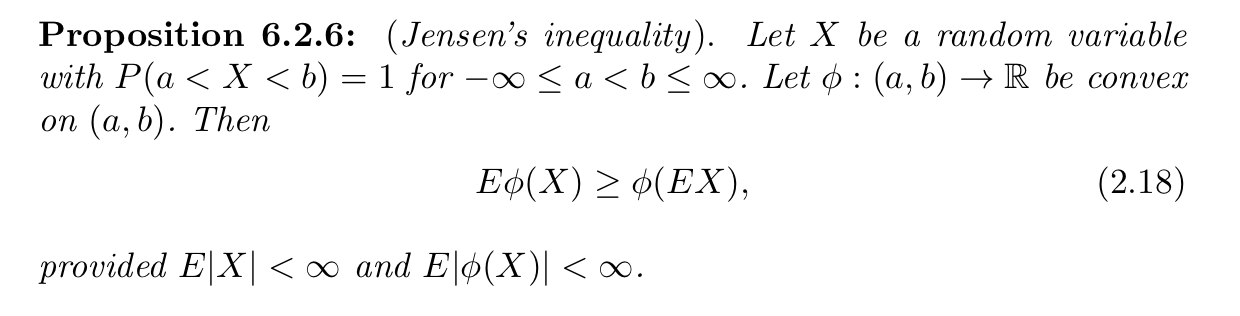
another

3.5.1.1. geometric inequality
Def:

3.5.1.2. Holder's inequality
Def:
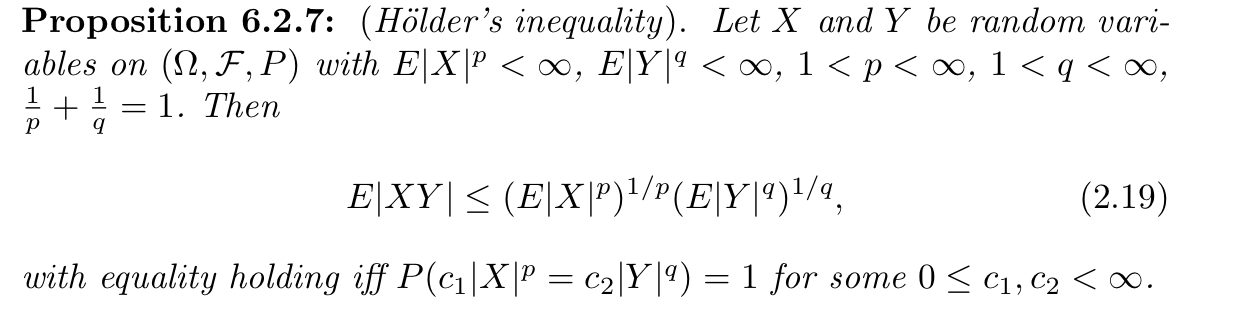
Note:

3.5.2. Cauchy-Schwarz inequality
Def:
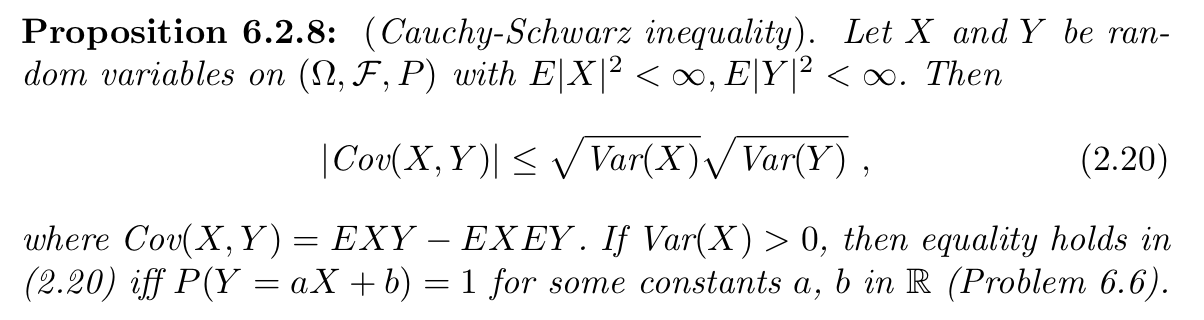
3.5.3. Minkowski's inequality
Def:
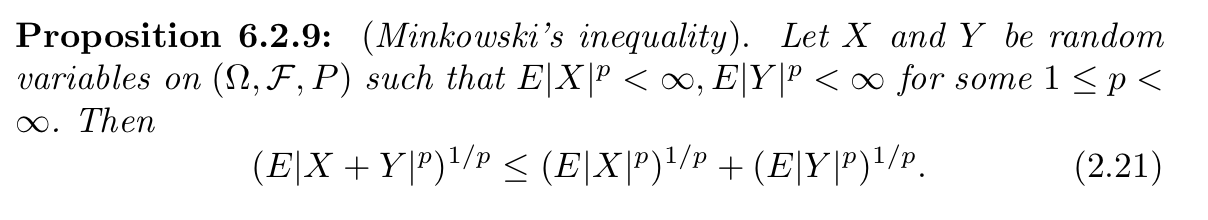
3.5.4. markov bound
Theorm: markov bound
Usage: measure the prob that of deviation will larger than e
s.t. V(X) \[ P(|X-E(X)| \geq e) \leq \frac{V(X)}{e ^{2}} \]

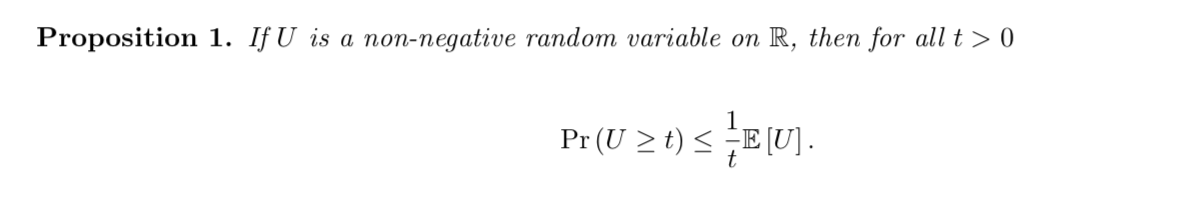
1-14

Example: that markov's only a very weak bound (1-14)

3.5.5. chebshev bound
Corollary : => chebshev bound

1-14

3.5.6. chernoff bound
Corollary: => chernoff bound
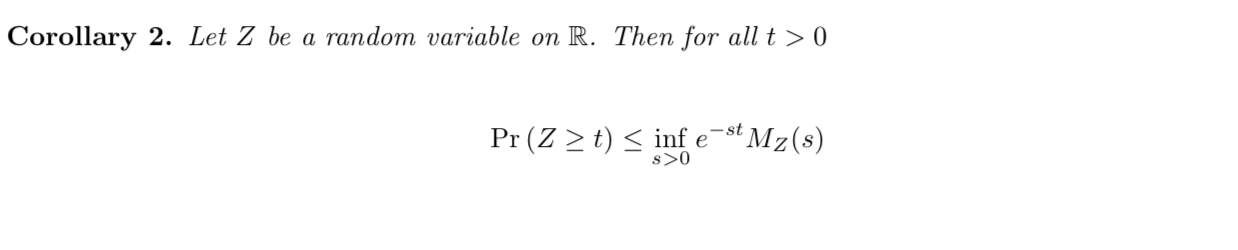
3.5.7. hoeffding bound
3.5.7.1. heffding bound
Intro: insights of hoeffding bound

Lemma: => bounds (used to prove hoeffding) (1-14)

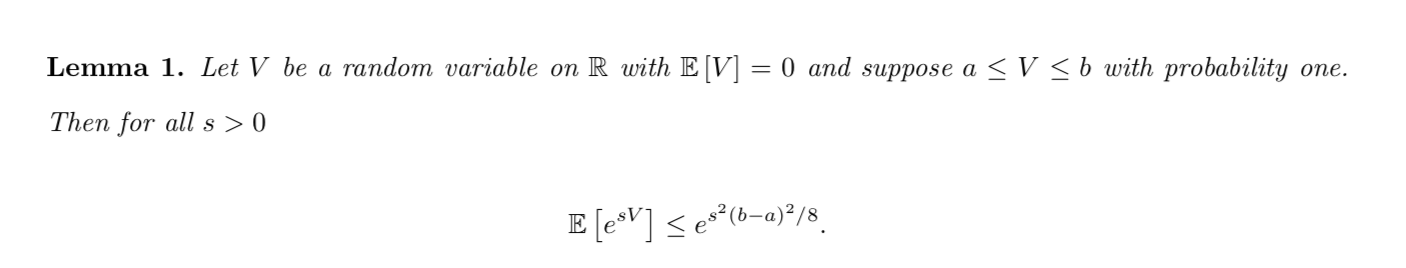
Proof:

Theorm:: => hoeffding's inequality (1-14)


(2-5)

Proof:

Example:

Corollary: => more bounds
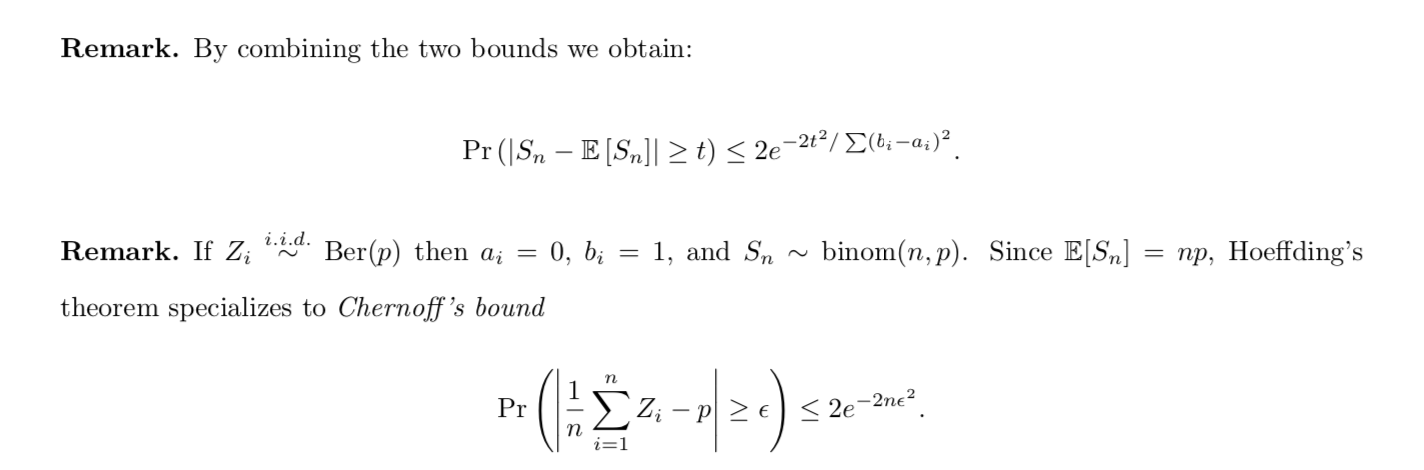
3.5.7.2. bound differences in equlity (1-15, 1-16)
Theorem: bound differences inequality (1-15)
Usage: adding a mapping on hoeffding bound

(1-16)

Proof:



Example: (1-16)

Example 2 : (1-16)
Usage: in this example we use sup(Eg-E^g) as a random variable.

Example 3 : (1-16) the loss function


3.6. limit theory
Def: tight & uniformly tight

Qua: suff & neck
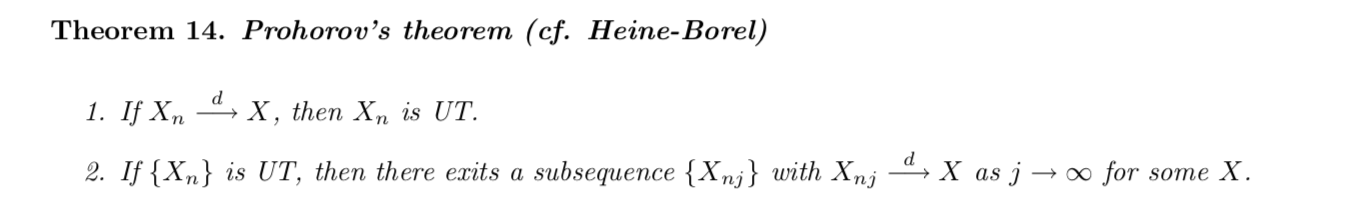
Theorm:: mono limit

Theorm: control limit

Theorm: different converges

Theorm: BC(3-6)

3.6.1. converges in distribution
Def: convergence in d
(2-1)

(2-10)

(2-10)

(book)

Note:


Qua: suff & necc

(2-1)

(2-1)

Qua: pn converge =>

Qua: operation
(book)

(2-1)

(2-1)

(2-2)

3.6.1.1. Helly theorem
Theorm: Helly, existence (book)

Proof: long
Theorm: Helly2, whether function still converge (book)

3.6.1.2. Levy theorem
Theorm: Levy, converge and cf (book)
Usage: special function & density one on one


Theorm: Levy backwards (book)

3.6.1.3. centrol limit theorem
Def: centrol limit theorem (sum of x --d--> gaussian) (book)

Theorm: sum of iid gaussain --d--> gaussian (book)

Note :

Theorm: sum of iid --d--> Gaussian (book)


Proof:

Theorm: sum of independent --d--> Gaussian (less strict condition) (book)


Theorm: sum of independent --d--> gaussian (less strict condition) (book)

3.6.2. converges in probabilty
Def: converges in probability
(2-1)

(3-6)
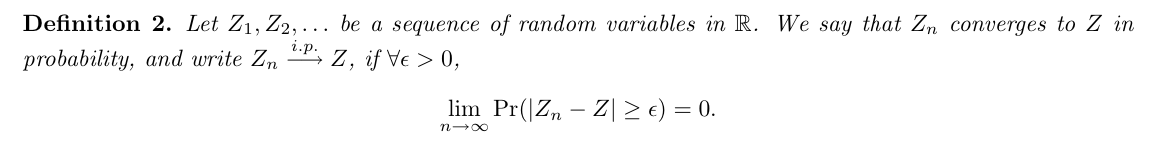
(book)


Note: why distribution not enough so include probability is nemeses

Qua: necc & suff (book)

Qua: E(zn-z) =>
(3-6)
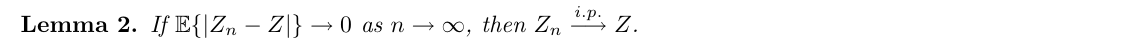
Proof: markov inequality
Qua: => d
(2-1)


(book)

Qua: operation
(2-1)

(2-2)

(book)

3.6.2.1. tight variables
Def: tight variables (2-1)

3.6.2.2. oh-pee
Def: Op,op (2-1)

Qua: operation

3.6.2.3. weak law of large numbers
Def; law of large numbers (book)

Theorm: sum of iid Bernoulli --p--> E (book)

(2-2)
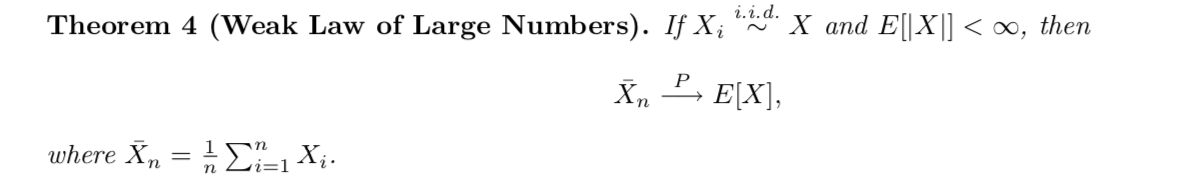
Theorm: sum --p--> E (less strict)

Proof:

Theorm: sum of invariant --p--> number (less strict ) (book)

Theorm: sum of iid --p--> number( more strict )(book)

3.6.3. converges in probabilty 1 / almost
Def:converge in probability.1
(2-1)

(3-6)
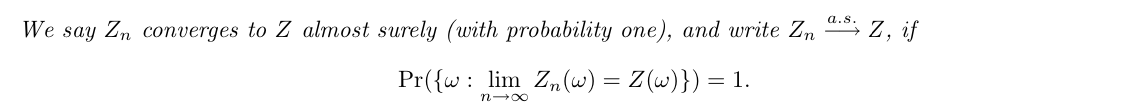
(book)

Note:

Qua: necc & suff (book)


Qua: P => (3-6)
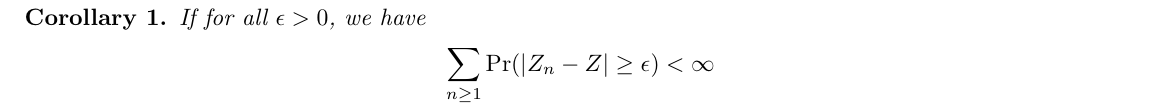
Proof: from Borel-Cantelli Lemma
Qua:P(a-b) => (book)

Qua: => P (2-1)

Qua: => lim(E|Xn-X|) (2-1)

Qua: => lowerbound(lim inf E|Xn|) (2-2)

Qua: => lim(E|Xn|) (2-2)

Qua =>lim(EXn) (2-2)

Qua: operation (2-1)

3.6.3.1. strong law of large numbers
Def: strong law of large numebrs (book)

Theorm:sum of bernolli --as--> number (book)

Proof: too long
Therom : sum of iid --as--> E. (book)

(2-2)

3.6.3.2. uniform law of large numbers
Def: sum of f(bernoll) --as--> number

3.6.4. convergence in r th mean
Def: converge in rth means
(2-1)

(book)

Qua: => p

3.6.5. continuous mapping theorem
Since weak convergence does not hold for all probability measures, we need conditions on the set C on which
the limiting random element concentrates.
Def: < (web)

Def: separable & regular
(2-10)

(web)

Theorem: continuous mapping theorem
(2-10)
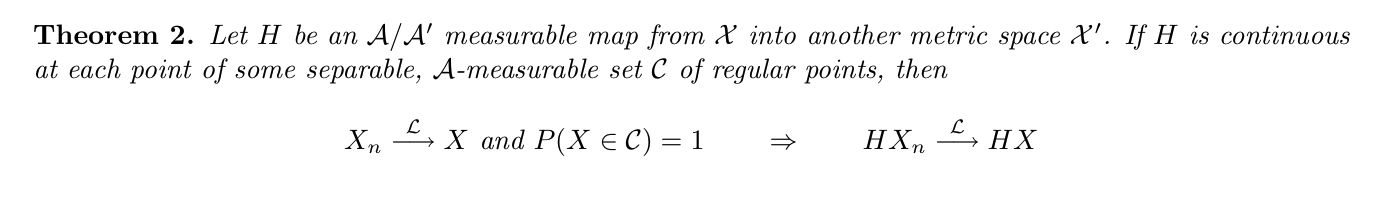
(web)

Theorem: stochastic equicontinuity
(2-10)
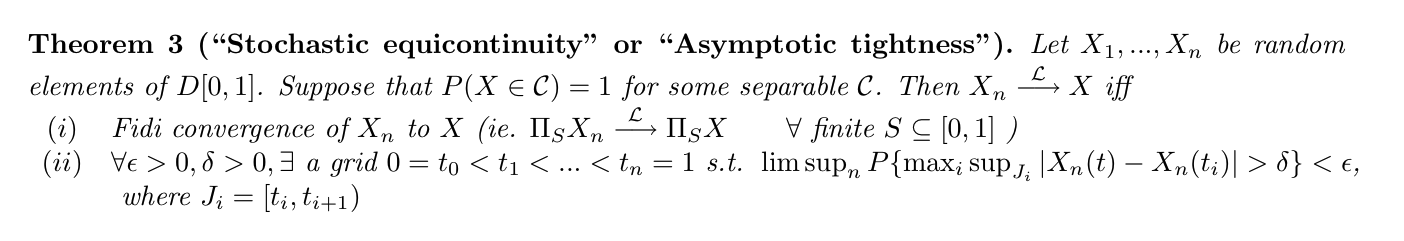
(web)

3.6.6. Donsker's Theorem(2-10,11)
Intro: why we need donsker's theorem (2-10)

Theorem:Donsker's Theorem v1(2-10)

Lemma: (web)

Theorem: Donsker's Theorem v2(2-11)

Proof: see archive
Theorem: Donsker's Theorem v3(2-11)
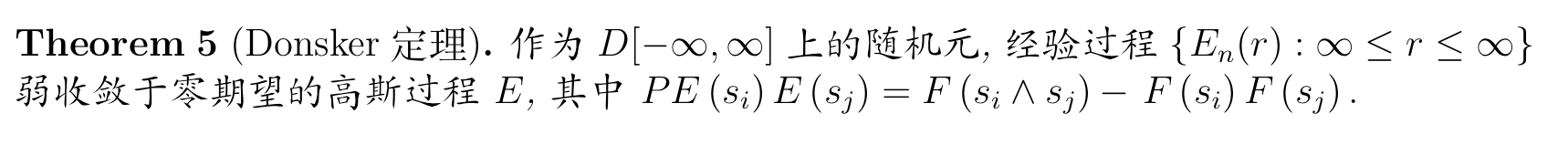
Proof: see archive
4. random vector
4.1. distribution
4.1.1. joint pdf
Def: joint pdf

4.1.2. margin pdf
Def:
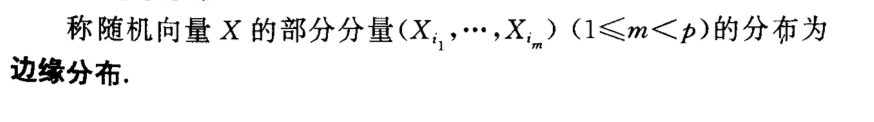

4.2. special functions
4.2.1. expectation
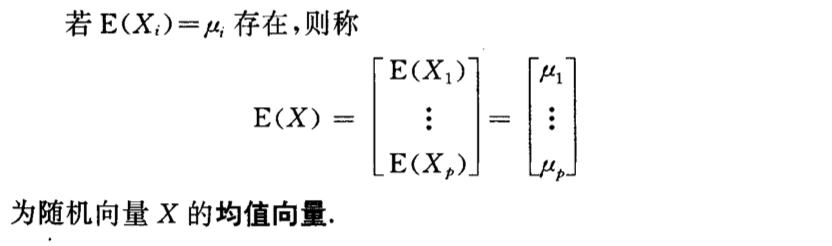
Def: E
- Qua: => basic
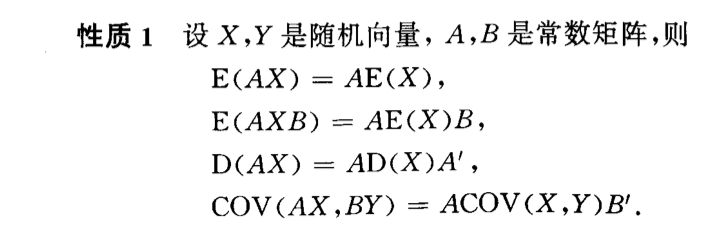
- Qua: => basic
4.2.2. covariance matrix
Def: covariance of X
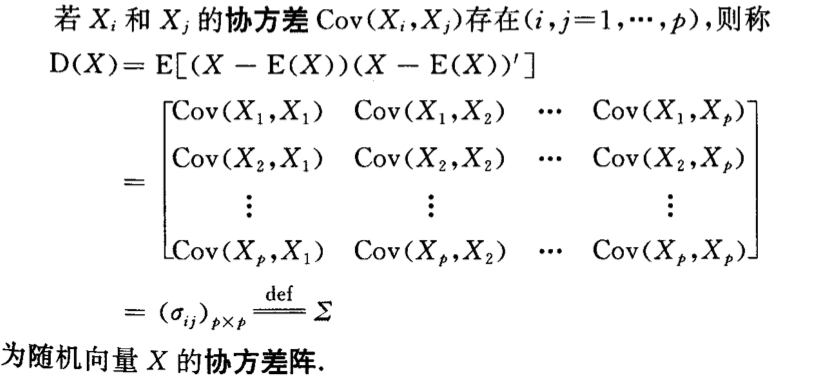
Qua: => non-negative
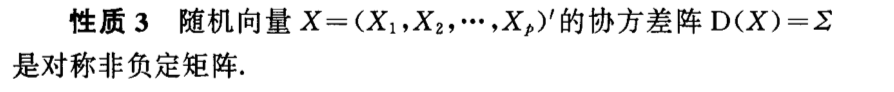

5. relationship between vectors
5.1. special functions
5.1.1. covariance matrix
Def: covariance

5.1.2. coefficient matrix
Def: coefficient matrix
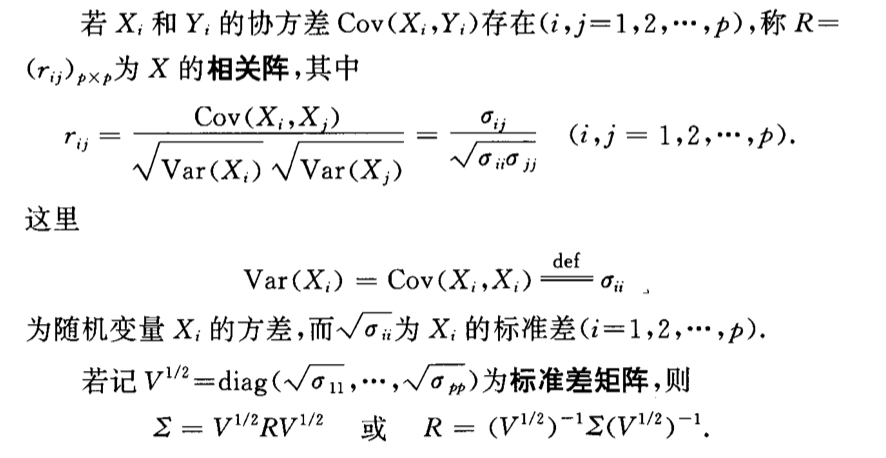
5.1.3. correlation coefficient
Def: correlation coefficient
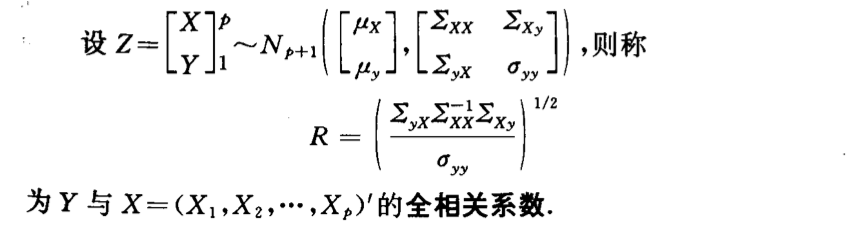
Def: skewed correlation coefficient
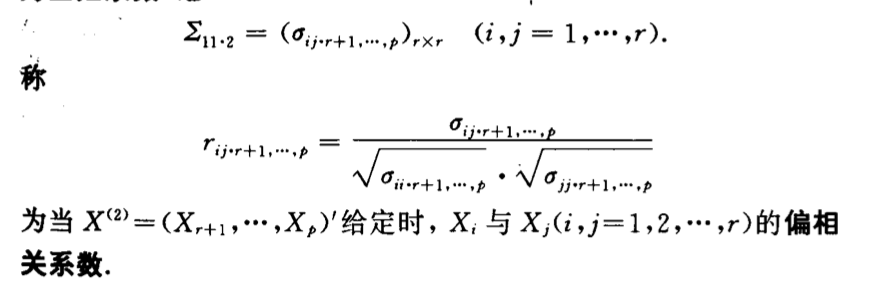
5.2. independence & correlation
5.2.1. conditional of itself
5.2.1.1. conditional pdf
Def: conditional pdf

5.2.1.2. conditional expectation
Def: con-E
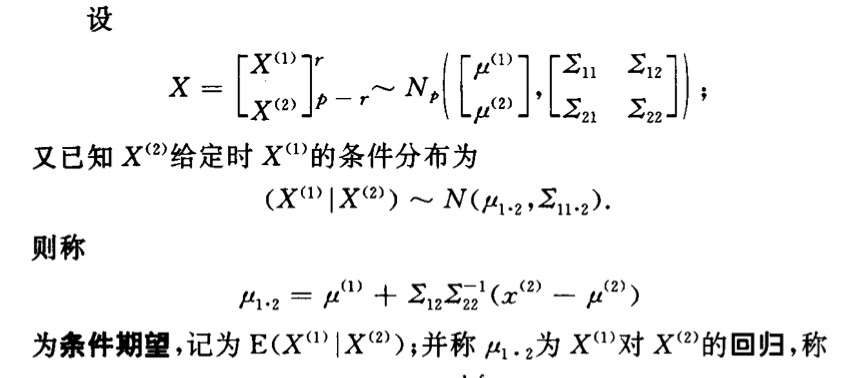
5.2.2. independence
- Def: independence
- Qua: => COV = 0
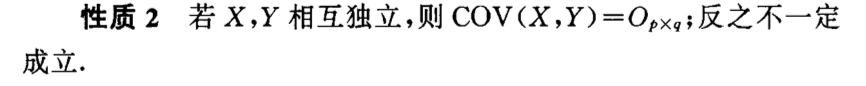
5.2.3. correlation
Def: correlation


