Mathematical Analysis Course Slides Notes
1. real number set
1.1. real number
Def: real number

Qua: real number basic quality

Qua: => real number absolute quality

Def:complex number

Qua: =>


Def: complex conjugate
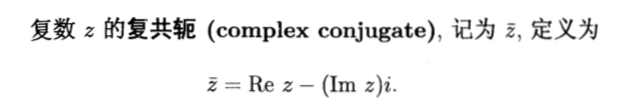
Def: absolute value
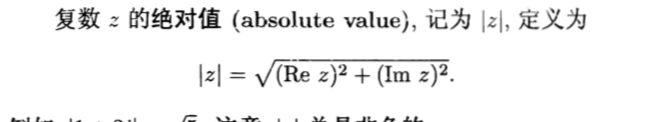
Qua: operation

1.2. range & neibor & bound of set
Def: range & neibor of set

Def: exact bound of set


Qua: => exact bound

2. function
2.1. one variable function
Def: function

Note:

Def: bound & function

Def: mono function

- Theorm: mono => inverse mono
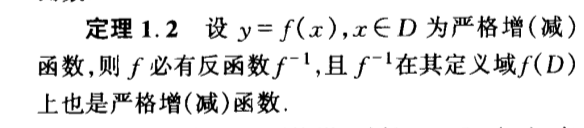
- Theorm: mono => inverse mono
Def: odd & function

Def: periodic & function

2.1.1. limit
2.1.1.1. limit
Def: limit of function to inf

Fig:

Def: limit of function to number

Fig:

Qua: 2 other functions larger & smaller => liim
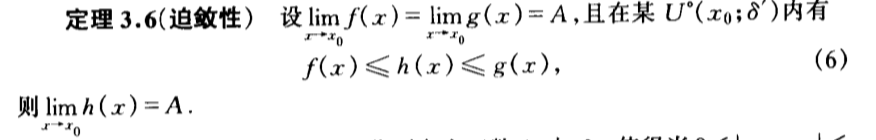
Qua: ~ => liim
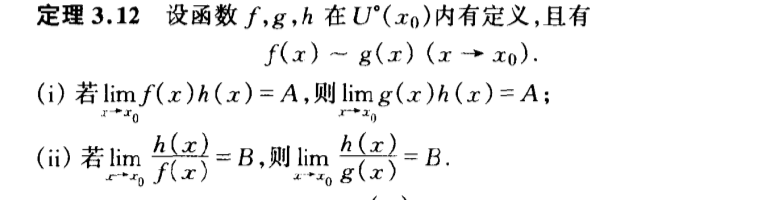
Qua: array => liim

Note:

Qua: f => liim


Example:

Example2

Qua: liim => only one
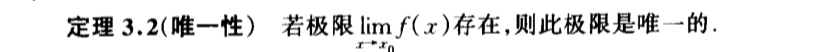
Qua: liim => bounded within a small range
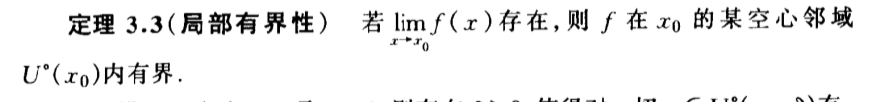
Qua: liim => sign not change within a small range

Qua: liim => keep order within a small range
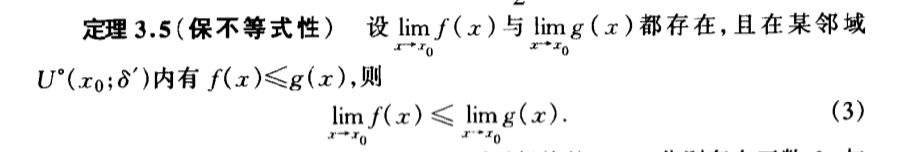
Qua: operation

Def: half way limit to number

Qua: mono => lim

Qua: mono => lim
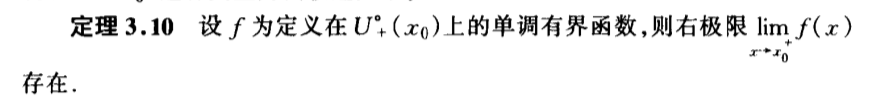
2.1.1.2. O & o
Def: inf small

- Qua: operation

- Qua: operation
Def: o

Def: --

Def: O


Def: ~
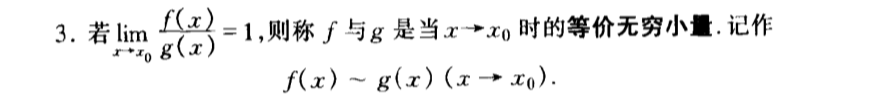
2.1.2. continuous
2.1.2.1. continuous
Def: continuous at one point
- continuous = limit exist + (limit = value)
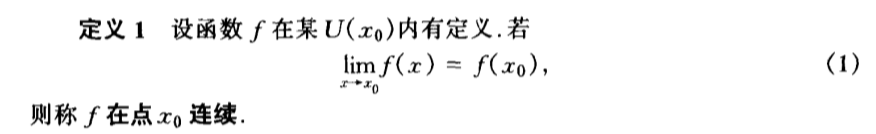
- def2

- def3

Qua: func => conti
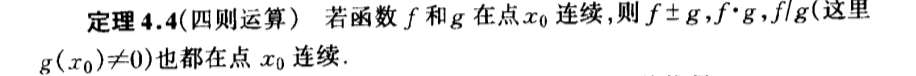
Qua: func => conti

Qua: limit & continuous
Usage: (1) conti => limit
(2) limit do not require x0, conti does
(3) f and limit can exchange order

Qua: conti => keep range
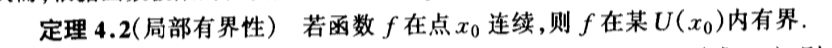
Qua: conti => keep sign within range

Def: left/right continuous
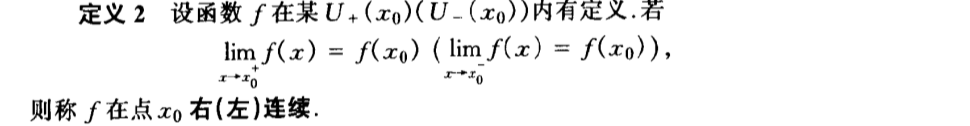
Qua: suff & necc

Def: break point

Def: can be wiped break point (no def)
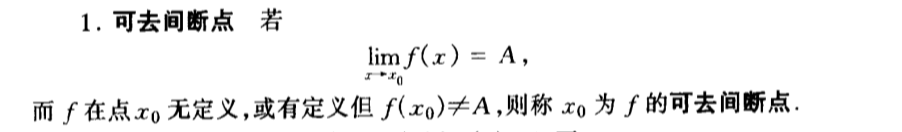
Def: jump break point (no lim)

Def: second break point (have def & lim but not equal)

2.1.2.2. continous function
Def: continuous function

Qua: conti => max/min

Qua: conti => f(x) = k

Qua: conti => inverse conti

Def: uniform continuous
Why: some conti func is too steep, like 1/x.

Note: Conti = choose a sigma(x, e) to make the gap < e
U-Conti = choose a sigma(e) to make the gap < e

Qua: suff
Def: several range continuous

2.1.3. derivation
2.1.3.1. def
Def: derivation

Qua: suff and necc

Qua: derble => some equation

Qua: derble => conti

Def: left/right der

Def: second order der
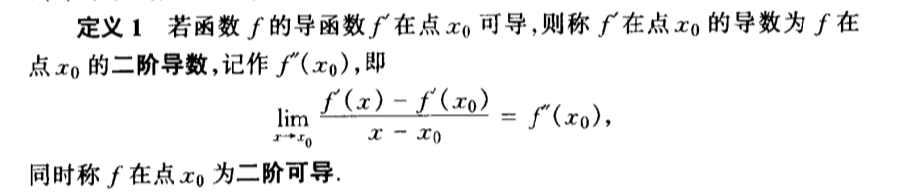

2.1.3.2. der function
Def: der function

Fig:

Qua: => der = k

Qua: => der = 0

Qua: => der = 0(k)


Qua: => der = g(x)

Qua: => der = c

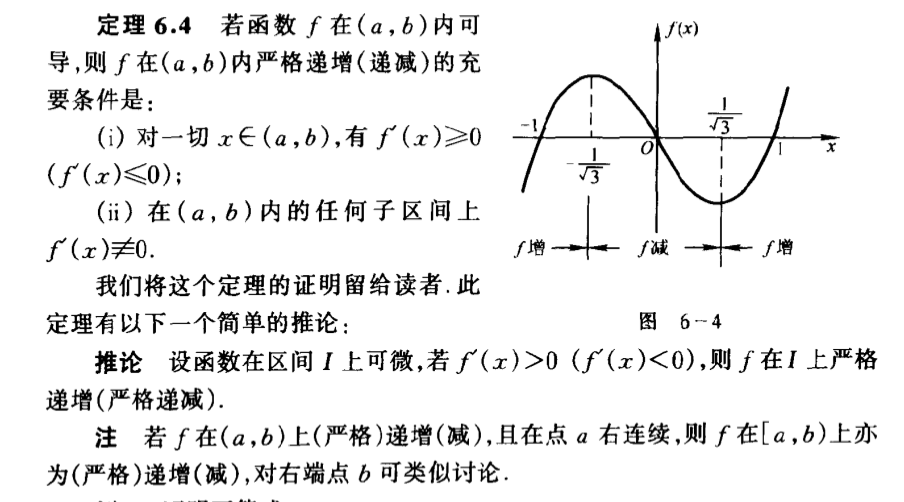
Qua: mono => der >=0

Qua: => der = c

Qua: => liim der = c


Qua: operation

Def: max/ min


Qua: => min/max

Qua: => min/max

Qua: => min/max

2.1.3.3. differential
Def: differential

Qua: derible + (A=f') = diffble

Qua: 恒成立的等式

Qua: operation(ddx=0 from deltadeltax = 0)( 可微情况下 dx = deltax)

Def: high order diff

2.1.3.4. taylor expansion
Def:

Qua: => taylor

Qua: => taylor

Qua: => taylor

Qua: => taylor

2.1.4. Riemann integration
- Def:origin

Qua: conti => origin

Qua: operation

2.1.4.1. non fixed integration
Def: not fixed integration

Qua: => integration

Qua: => integration
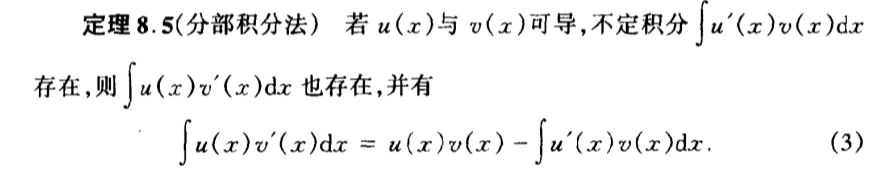
Qua: devotion => integration


Qua: sin => integration

Qua: => integration

Qua: operation
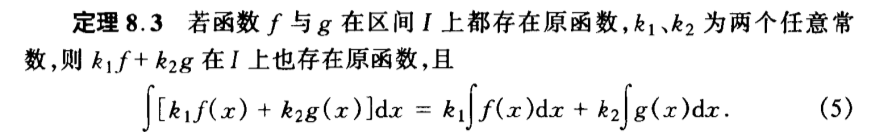
2.1.4.2. fixed integration
Def:


Note:


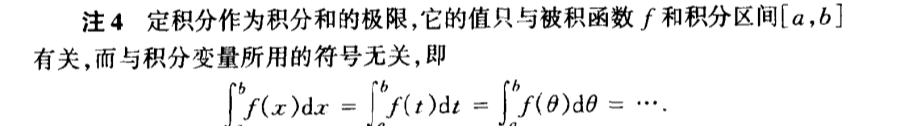
Fig

Qua: => integration

Note:

Qua: => integration
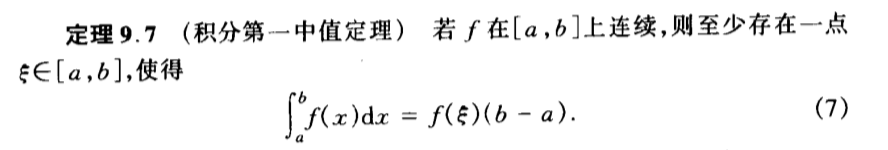
Qua: => integration

Qua: => integration
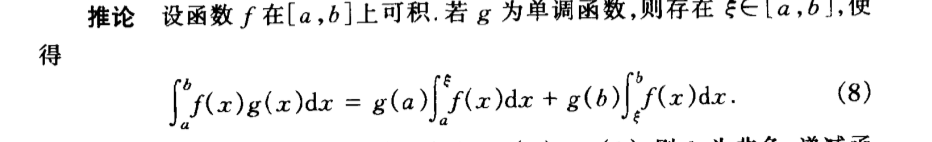
Qua: => integration
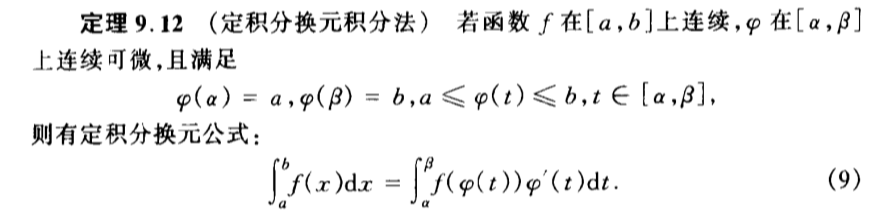
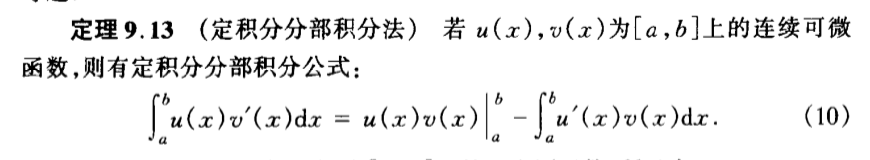
2.1.4.2.1. integratable on [a,b]
Def: integratable on [a,b]
Qua: => intble


Qua: => intble

Qua: => intble
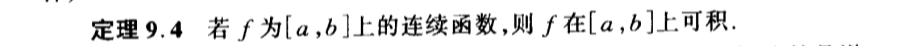
Qua: => intble

Qua: => intble

Qua: intble => bounded
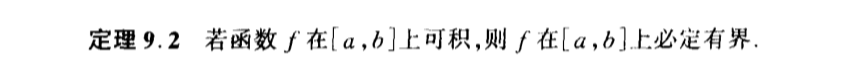
Qua: intble =>

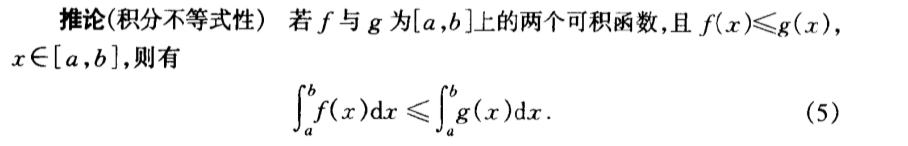
Qua: intble =>

Qua: intble =>
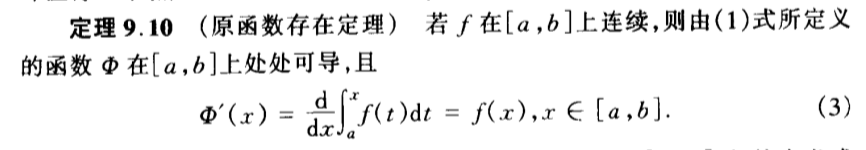
Qua: intble =>

Qua: operation
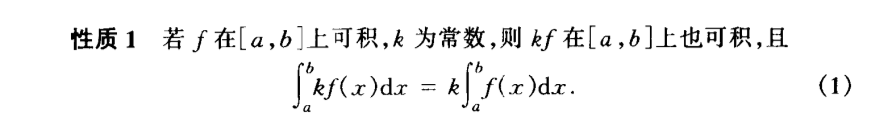
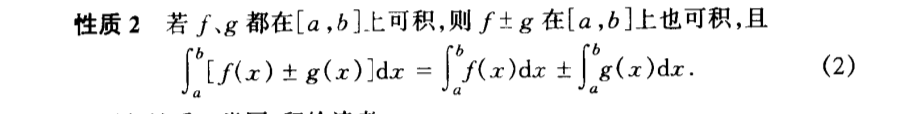
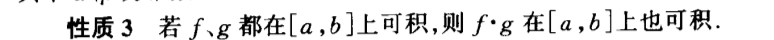
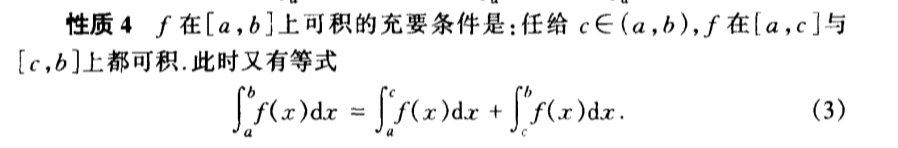
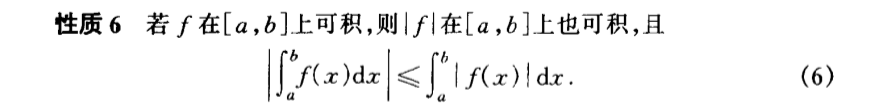
2.1.4.3. abnormal integration
Def: inf abnormal

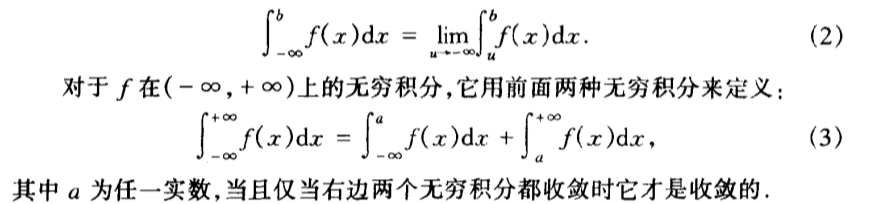
Note:

Fig:

Qua: suff & necc of convergence
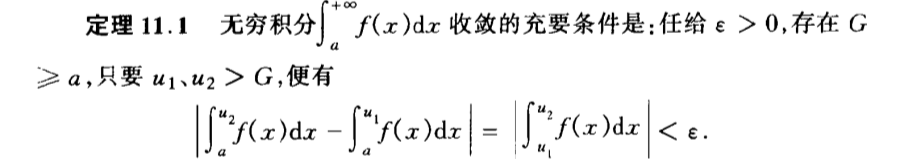
Qua: => convergecy

Qua: => convergency

Qua: operation
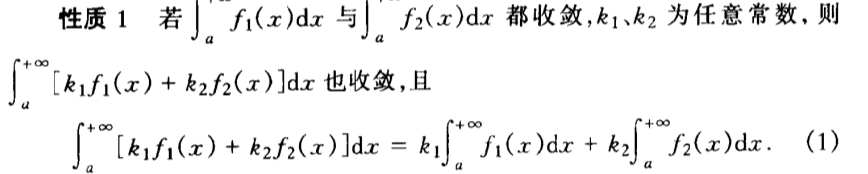

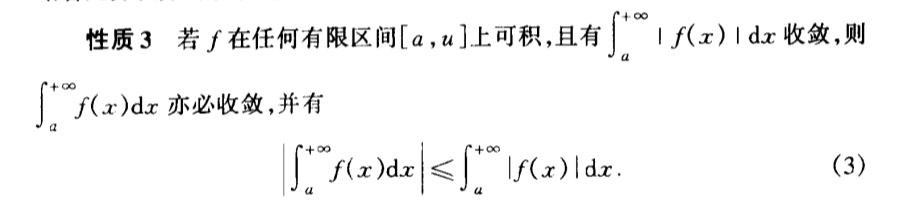


Def: break point abnormal integration

Note:

Qua: suff & necc
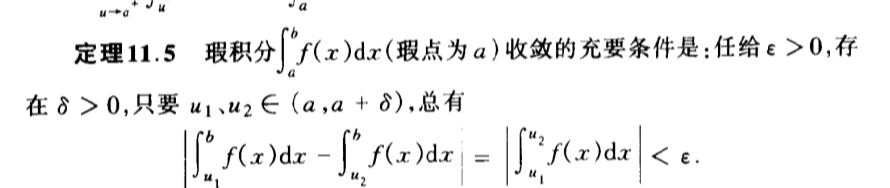
Qua: operation
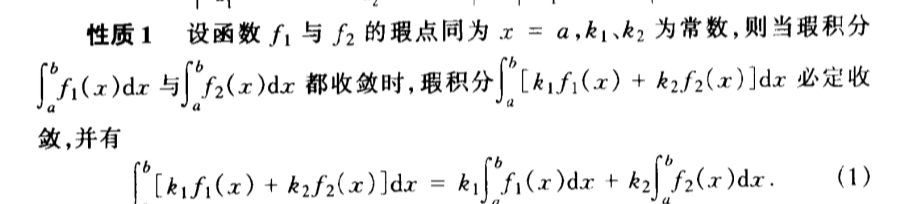
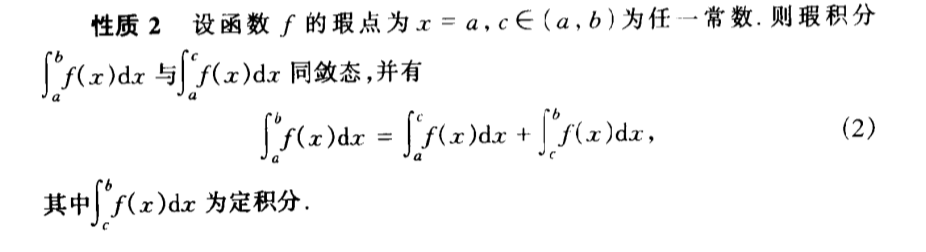


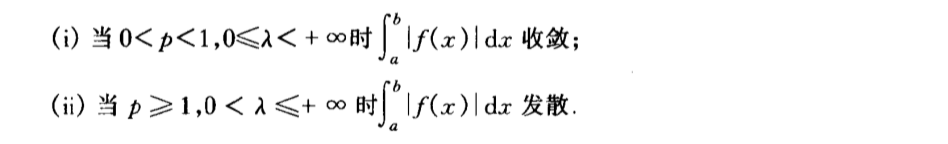
2.2. multi variable function
2.2.1. limit
2.2.2. continuous
2.2.3. derivation
1 to 1 textbook
1 to X/M https://blog.csdn.net/weixin_38278334/article/details/83028794
X/M to X/M https://zhuanlan.zhihu.com/p/24863977 here is to mention that, the definition of 1 to X/M is different from X/M, we are more inclined to refer 1 to X/M as \(\triangle\), and the other as derivatives.
2.2.4. hidden variable
2.2.5. integration
2.2.5.1. parameter nomral integration
Def:
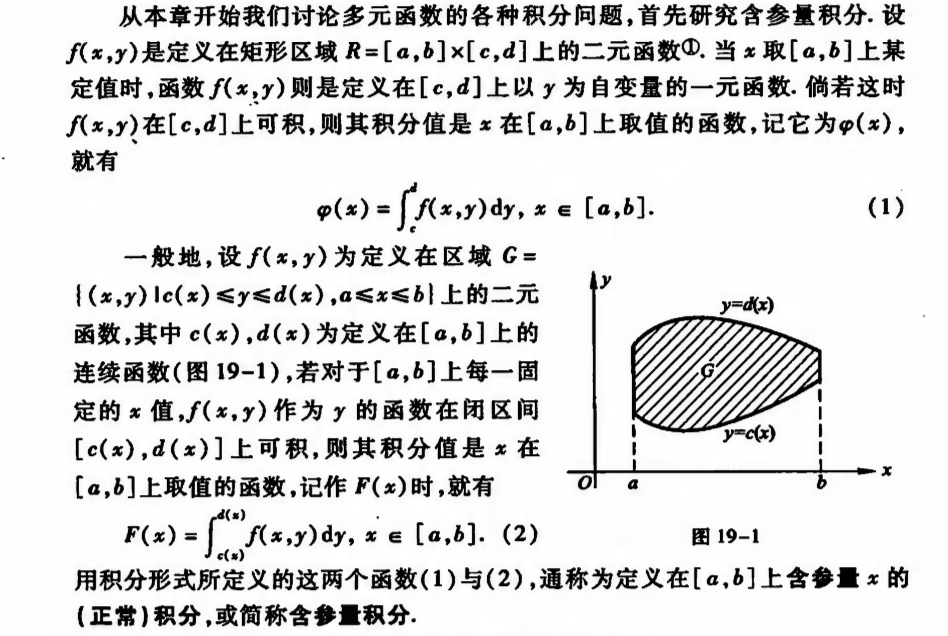
Qua: => conti
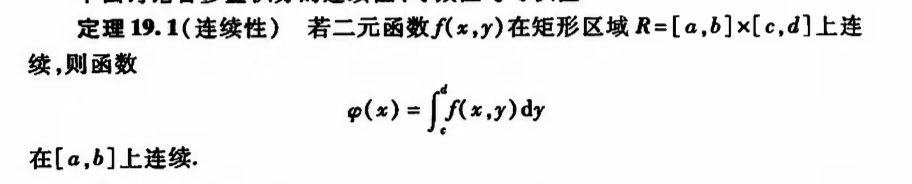
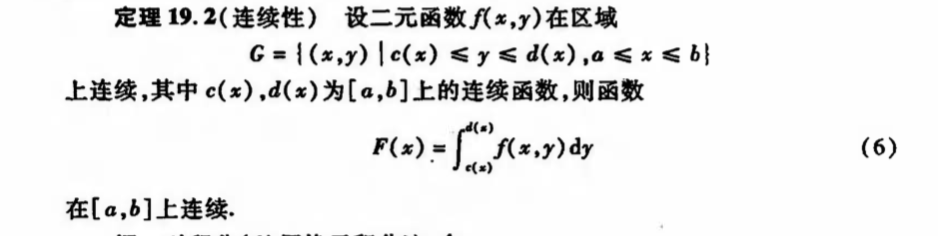
Qua: => diffble
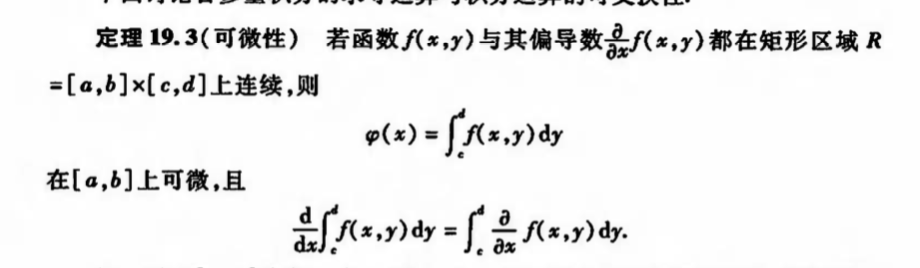

Qua: => intble

Qua: => order changeble
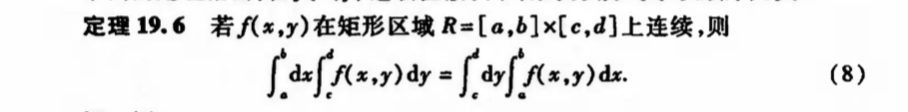
2.2.5.2. parameter abnomral integration
2.2.5.2.1. def
Def:

Def: uniform convergency

Qua: suff & necc

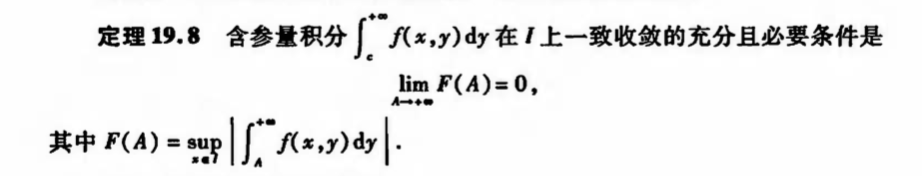
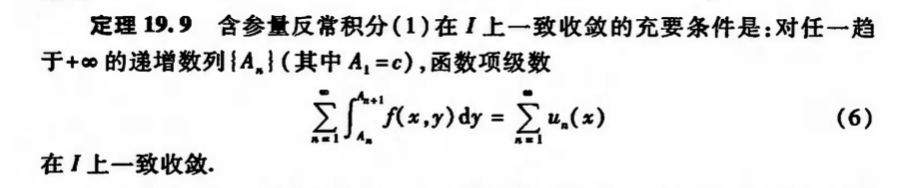
Qua: => converge

Qua: converge => conti

Qua: converge => exchange order(conti)

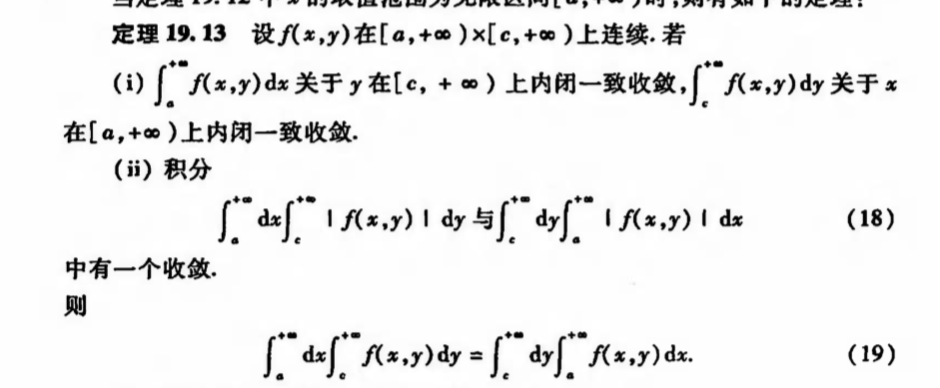
Qua: converge => diffble
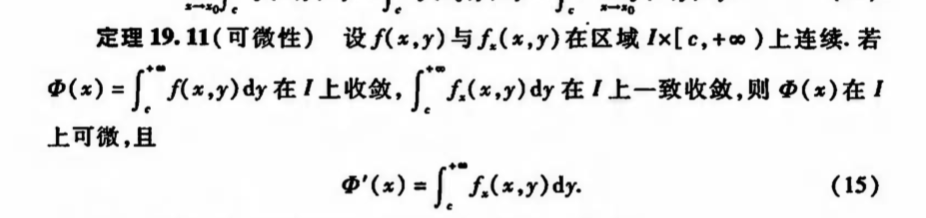

Qua: converge => intble
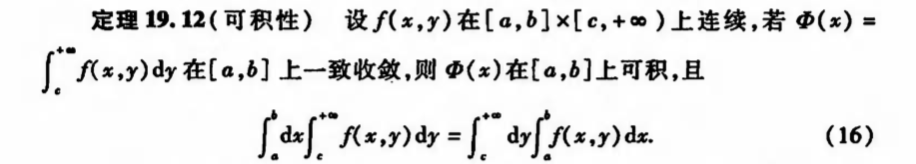
2.2.5.2.2. gamma & beta integration
Def: gamma
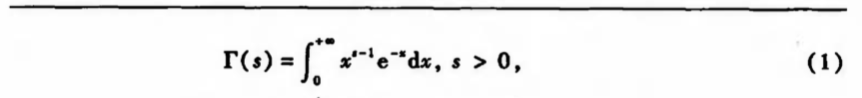

Fig:
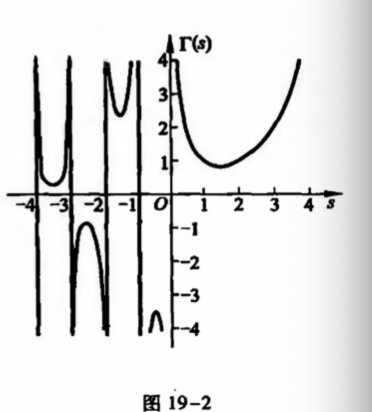

Qua: gamma => diffble & conti

Qua: gamma => equation

Qua: gamma => tranform

Def: Beta
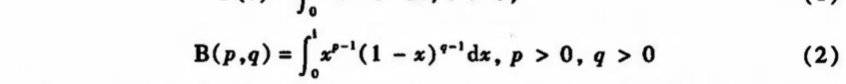

Qua: beta => conti

Qua: beta => equatiom
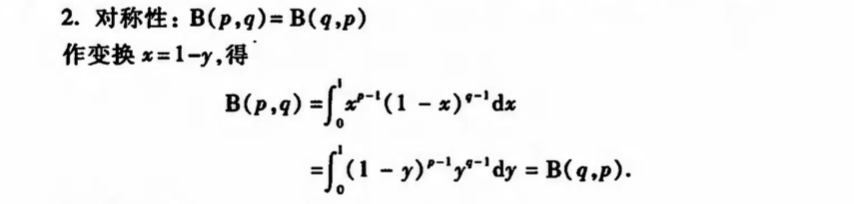
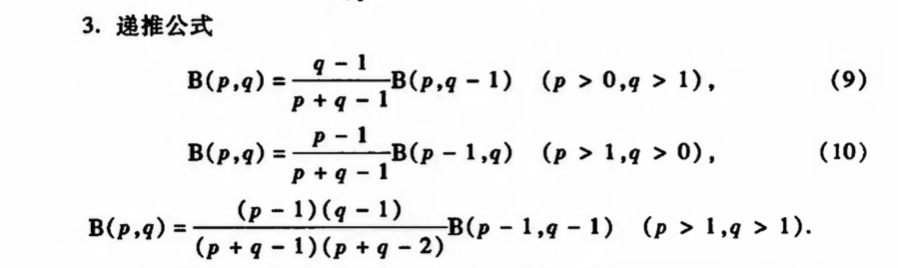
Qua: beta => transform

Qua: beta & gamma

2.2.5.3. curve integration
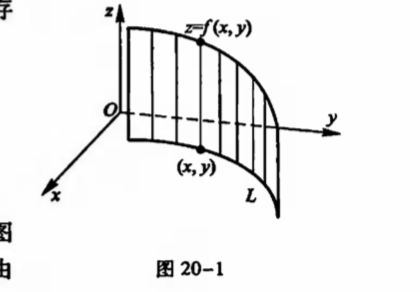
Def: first curve integration

Fig:

Qua: => integration
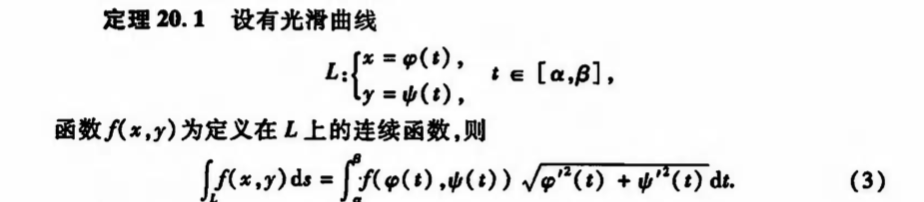
Qua: intble =>

Qua: intble => 路线无关性

Def: second curve integration


Note:

Qua: => integration

Qua: operation
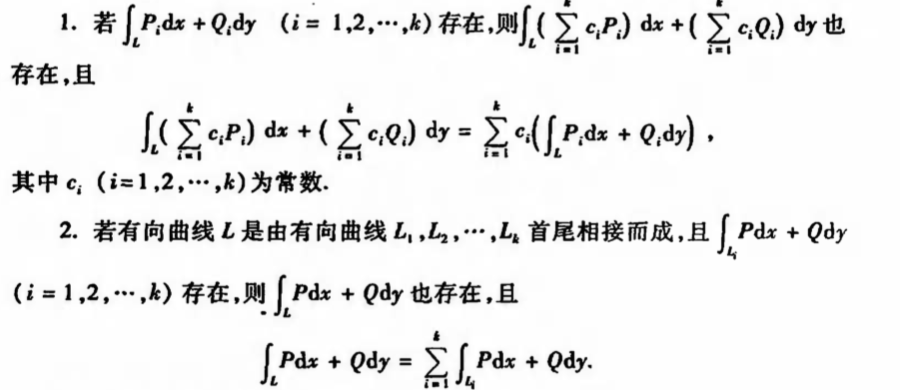
2.2.5.4. muliple integrate
Def:

Qua: suff & neck




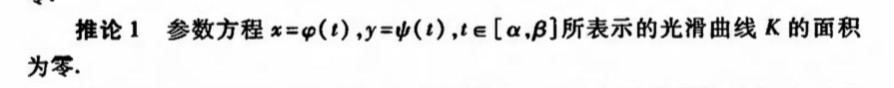
Def: multi integration

Note:

Qua: suff & necc

Qua: => intble

Qua: intble =>

Qua: => integration
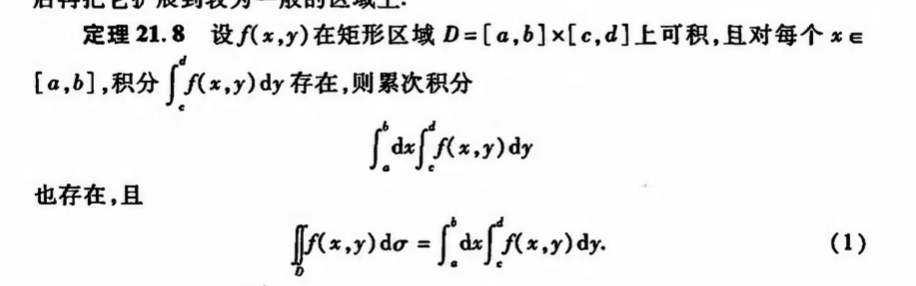
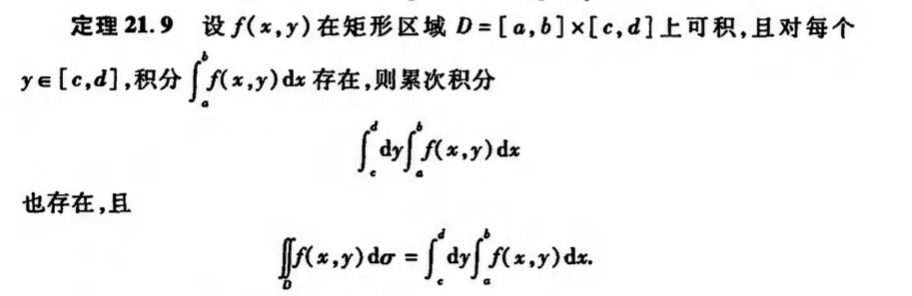
Qua:Green, => integration

Qua: operation


3. array or series
3.1. number array/series
12
3.2. function array/series
3.2.1. function array
Def: function array

3.2.1.1. convergence
Def:

3.2.1.2. uni convergence
Def:

Note: visualization & why it's important

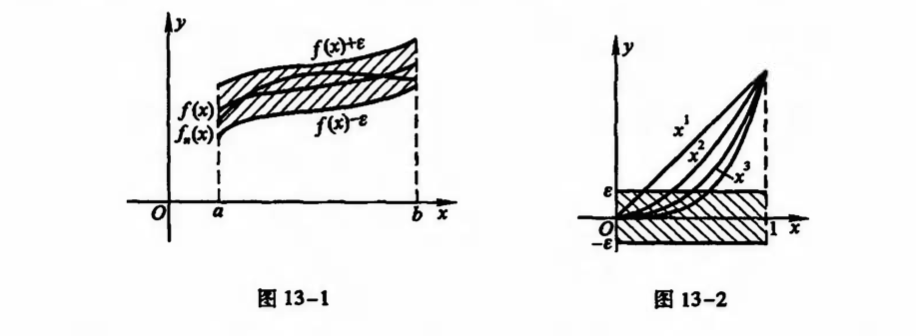
Qua:caughy =>

Note: same thing
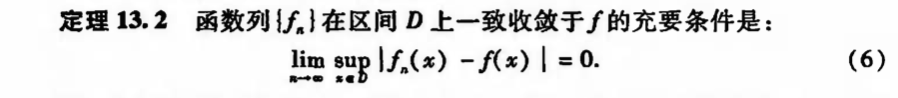
Corollary:

3.2.1.3. f induced by function array
3.2.1.3.1. limit
Def: limit

Note; limit & limit exchange


3.2.1.3.2. continuous
Def: continuous
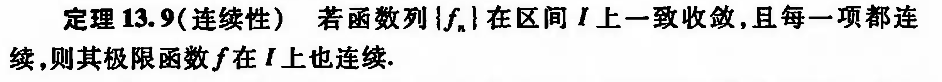

3.2.1.3.3. derivation
Def: derivable


Note: limit & deri exchange

3.2.1.3.4. Riemann integration
Def : integrable
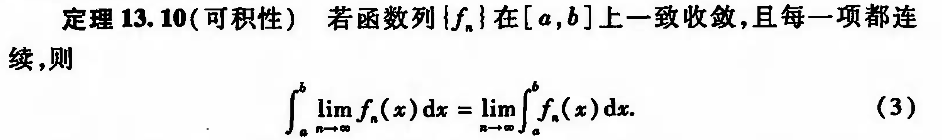
Note: limit & intg exchange

3.2.2. function series
Def:

3.2.2.1. convergence
Def:

3.2.2.2. uni convergence
Def:
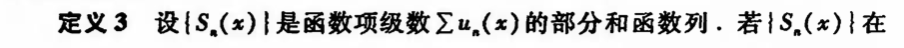

Qua: necc & suff

Note: same thing
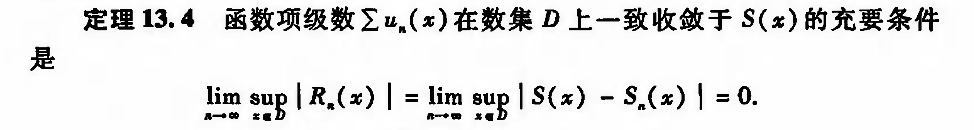
Qua: some =>

Qua: some =>


Qua: some =>

3.2.2.3. f induced by function series
3.2.2.3.1. continuous
Def:

Note: sum & limit

3.2.2.3.2. derivation
Def:

Note: sum & deri

3.2.2.3.3. Riemann integration
Def:
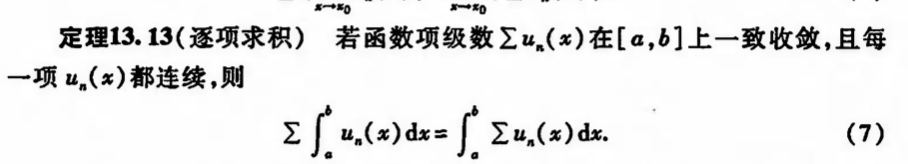
Note: sum & intg

3.2.3. power series
Def:

3.2.3.1. convergence
Def:
Qua:abel =>

Note:

Qua: =>

Note: same thing

3.2.3.2. uni convergence
Def:
Qua: =>

Qua: =>

Qua:
3.2.3.3. f induced by power series
3.2.3.3.1. continuous
Def: continuous

3.2.3.3.2. deri & integral
Def:

Corollary:


3.2.3.4. computation of coefficient
Def: equavalence

Theorem: operation
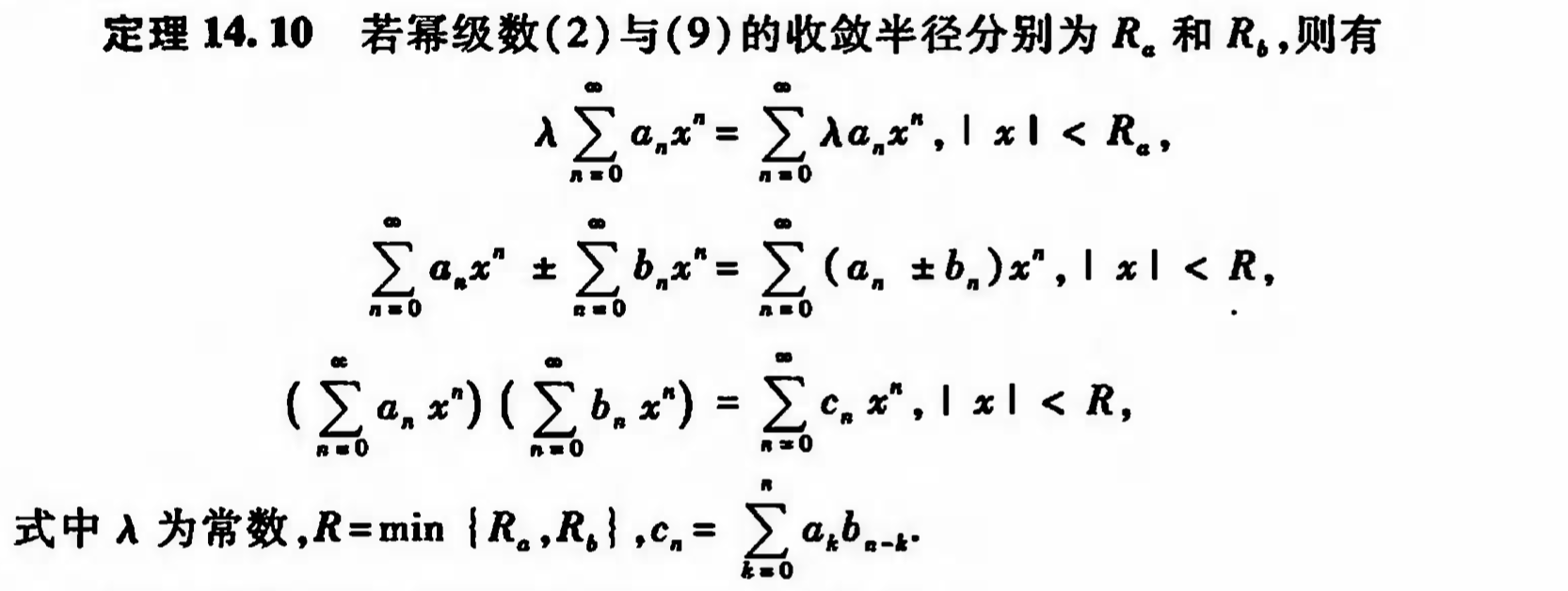
3.2.3.5. taylor series
Def: taylor series
Usage: expansion without Rn

Def: generated by taylor series
Usage: when f = taylor series

Qua: same => exist

Qua: => uniqueness

3.2.4. fourier series
Def: tri series

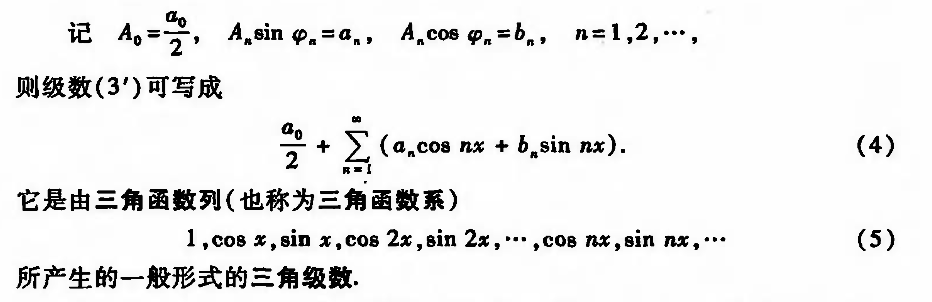
Qua: convergence

Def: fourier series

Note:

Qua: =>
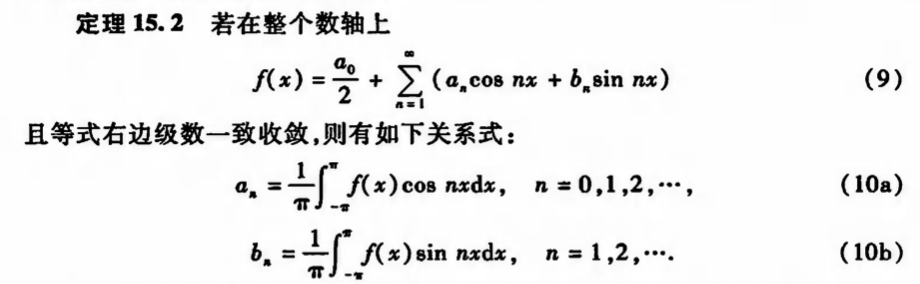
3.2.4.1. convergence
Def: smooth

Qua;

Def: convergence
Qua:
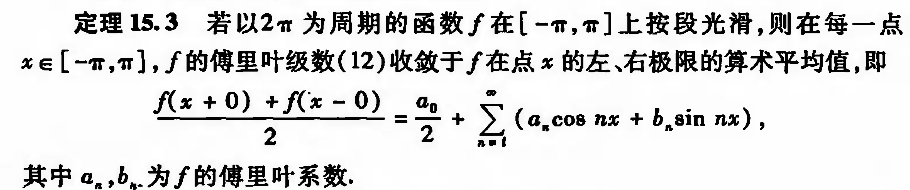
Qua: 2 \(\pi\) -> 2l

Qua: single / not