Linear Algebra

Linear Algebra Course Slides Notes

1. space

• Note: figure of different spaces

  

• Note: brief intro to various spaces

  

1.1. vector space （linear space）

• Def: vector space ( V on F )

  

  

  Note:

  

  Example:

  

  • Qua: => qualities

    

  • Qua: => only one adding element

    

  • Qua: => only one adding invert

    

  • Qua: =>0v=0

    

  • Qua: => ao=0

    

  • Qua: => (-1)v = -v

    

1.1.1. subspace & sum (直和)

1.1.1.1. subspace

• Def: subspace

  

  • Qua: 3 conditions =>

    

    Note:

    

  • Qua: => finite

    

  • Qua: => dimension

    

  • Qua: => dimension

    

1.1.1.2. sum

• Def: sum

  

• Def: direct sum

  

  • Qua: necc & suff (multiple)

    

  • Qua: necc & suff (2 subspace)

    

  • Qua: finite =>

    

  • Qua: dimentiosn =>

    

1.1.2. linear combination & span

1.1.2.1. linear combination

• Def: linear combination

  

  • Qua: necc & suff

    

  • Qua: necc & duff

    

    • Corollary:

      

  • Qua: necc & suff

    

  • Qua: => rank

    

1.1.2.2. span

• Def: span

  

  • Def: be spanned by

    

1.1.2.3. linear independent

• Def: linear independent

  

  • Theorm: necc & suff of dependent

    

  • Theorm: rank =>

    

  • Lemma : => span

    

  • Theorm: => length

    

• Def: largest indepent group

  

1.1.3. basis

• Def: basis

  

  

  • Qua: necc & suff

    

  • Qua: every spanned group =>

    

• Corollary: every finite space =>

  

  • Qua: every independent =>

  

• Qua: every length spanned group =>

  

• Qua: every length independent =>

  

• Def: dimension

  

  • Qua: finite =>

    

  • Theorm: for map-space dimension =>

    

  • Theorm: subspace dim =>

    

    • Corollary: => no dandi

      

    • Corollary: => no mandi

      

    • Corollary: => no solution

      

• Theorm: => relationship with matrix rank

  

  

1.1.3.1. othonomal basis

• Def: othonomal

  

  • Qua: => independent

    

    

• Def: othonomal basis

  

  • Qua: Gram-Schmdt convert to otho =>

    

    Algorithm:

    adjoint

    

  • Qua: => xxx

    

1.2. metric space

• Def: distance space

  

1.2.1. separable

• Def: separable

  

  • Lemma: separa => Borel = Borel0

    

• Def: Borel set

  

  • Def: Borel 0 set

    

• Def: measurable map

  

  • Qua: necc & suff

    

• Def: projection map

  

  Note

  

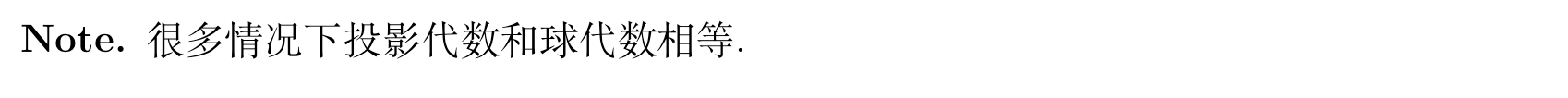
• Def: RCLL function

  

  Note:

  

• Qua: some statements

  

1.3. inner product space

1.3.1. inner product

• Def: inner product：The inner product operator measures the similarity between vectors

  

  Example: very important, we see f, g as very long vectors(infinite), and <f, g> is basiclly the sum of infinite vectors.

  

  Example: very important example here, fourier function

  define infinite basis functions

  

  prove that basis function are orthogonal

  

  any f can be written as linear combination of basis functions (proof: using orthogonal)

  

  compute coefficient : use orthogonal

  

  

  • Qua: necc & suff

    

  • Qua: => quality

    

    

  • Qua: => quality

    

    

• Def: orthogonal

  

1.3.2. norm

• Def: norm

  

• Def: norm

  

  • Qua: necc & suff

    

  • Theorm: => Cauchy-Schwarz Inqueality

    

  • Theorm: Triangle inequality

    

  • Theorm: Parallelogram inequality

    

  • Theorm: Pythangorean

    

1.3.3. inner product space

• Def: inner product space

  

  Example:

  

  

  • Qua: => T=0

    

  • Qua: => continuous

    

1.3.4. orthogonal complement

• Def: orthogonal complement

  

  • Qua: => V=a+b

    

    • Corollary: => invertable

      

• Def: orthogonal projection

  

  • Qua: => qualities

    

  • Qua: => norms

    

1.3.5. linear functional & adjoint

• Def: linaer funcitonal

  

  • Qua: =>

    

• Def: adjoint

  

  • Qua: =>

    

    

  • Qua: =>

    

  • Qua: =>??

    

1.3.6. self-adjoint function & normal function

• Def: self-adjoint function

  

  • Qua: necc & suff

    

  • Qua: => egenvalue

    

  • Qua: => T = 0

    

• Def: normal function

  

  • Qua: necc & suff

    

  • Qua: => egenvalue

  

  • Corollary:

    

1.3.6.1. complex space

• Theorm: complex spectral theorm, necc & duff

- Corollary: => invertible

![](https://tva1.sinaimg.cn/large/006y8mN6ly1g96vbl0bl9j31240ammzc.jpg)

• Corollary: => egvalue

  

1.3.6.2. real space

• Theorm: real special thoemr, necc & suff

  

  • Qua: => direct sum

    

• Theorm: necc & duff of [norm but not self]

  

• Theorm: necc & suff of norm

  

• Theorm: necc & suff of norm

  

1.3.6.3. positive function

• Def:positive function

  

  • Theorm: necc & suff

    

  • Theorm: => root

  

• Def: square root

  

1.3.6.4. isometry function

• Def: isometry

  

  • Qua: necc & suff

    

  • Qua: necc & suff

    

  • Qua: necc & suff

    

  • Theorm: polar decomposition

    

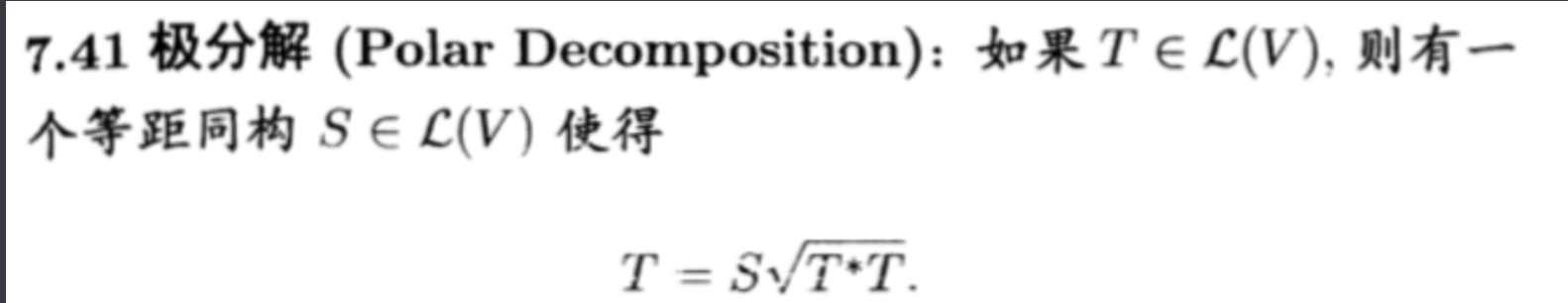
• Def: singular value

  

  • Theorm: => singular value decomposition

    

1.4. hilbert space

• Def: hilbert space

  

  • Def: complete space

    

  Example: of hibert space

  

1.4.1. kernel (1-8 & web)

• Def: kernel (1-8)

  

• Def: kernel (web)

  

  Example:

  

• Def: kernel

  defiinition 3: web

  

  Example: of \(\phi\)

  

  • Qua: => quality of kernels

    

    Proof:

    

  • Operation: (1-9), below are all kernels.

    

    

    

  • Operation: (web)

    

    

    

    

1.4.2. reproducing kernel hilbert space (1-8 & web)

• Def: reproducing kernel hilbert space ( web )

  rkhp is a hilbert space with reproducing property, which the basis eigen function form the basis of it . Given kernel function-X space, we can get eigen basis-rkhp( - means that it is one on one); it may be confusing that hilbert space can be function space / vector space , but here we only consider function space.

  

• Theorem: Mercer theorem(web), kernel related to X space, eigenfunc/vec related to L(x) function space. kernel function can be expressed in combinition of eigen functions.

  

  Proof:

  from eigen value, get the following (see K(x,y) as infinite matrix, x implies column, y is row.

  

  prove orthogonal, them we can use eigen decomp to prove the theorem.

  

• Def: reproducing property (web)

  for this type of inner product, we have reproducing property

  

  

  Proof:

  present f as combinition of eig functions

  

  s

  from mercy theorem, we get (there should be a T at the end)

  

  therefore, from definition, we get

  

• Def: kernel trick( web)

  now that we have get kernel-X and eigen function-rkhp, we define a rkhp-mapping: \(\phi(x)\) is a function X-> H, K(x, .) may seem confusing but it is a function from X-> H as well, the dot means that the place

  

  then we get

  

  Example: in this example, \(\phi(x)\) is the coordinate of feature space(which is a function hilbert space), there should be a H at the end of \((x1, x2, x1x2)^{T}_{H}\); the function space basis functions are:\(\psi _{1}(.) = e1(.)\), \(\psi _{2}(.)=e1(.)\) , \(\psi3(.)=e1(.)*e2(.)\), but we do not need to know the exact hilbert space it is projected to in most cases.

  

• Def: reproducing kernel hilbert space (1-8)

  this is the same. rkhs is here have to be a function space(X->R), which every element satisfy reproducing property.

  

• Def: reproducing kernel hilbert space (1-8)

  same thing .

  

• Def: kernel trick (1-8)

  kernel(x, y) = <\(\phi(x)\), \(\phi(y)\) >, very important stuff here!!

  

  Proof:

  the thing here is different from web version. we change hilbert space basis function to k(., xi), \(i=1...n\), I imagine that this is merely a change of basis. \(\phi(x):X\to R ^{X}( R^X\text{ means function from X to R} )\)

  

• Theorem: Mercer theorem(1-8)

  Usage: we can get something more from this version. we can approximate \(\phi\) by a finite dimensional map.

  

  Proof: none

  Note: 这个是mercy定理的直观证明：

  

  

  Example: SVM

  

1.4.3. representing therom (1-9)

• Theorm: representer, which shows that even in an infinite dimensional reproducing kernel Hilbert space, the minimizer f∗ can be repre- sented as an (at most) n-dimensional linear combination of kernel functions.

  Usage: We can generalize this and prove a simple but powerful theorem called the “Representer Theorem,” which shows that even in an infinite dimensional reproducing kernel Hilbert space, the minimizer f∗ can be repre- sented as an (at most) n-dimensional linear combination of kernel functions.

  

  Proof:

  

  

• Def: translation-invariant kernel

  

  

  Example: fourier expansion, we define a invariant k(x), then we see what the original kernel is.

  

  

1.5. measure space

see measure theory

1.5.1. L2 space

• Def: L2 space (2-4) function space

  

1.5.2. Lp space

• Def: Lp function space

  

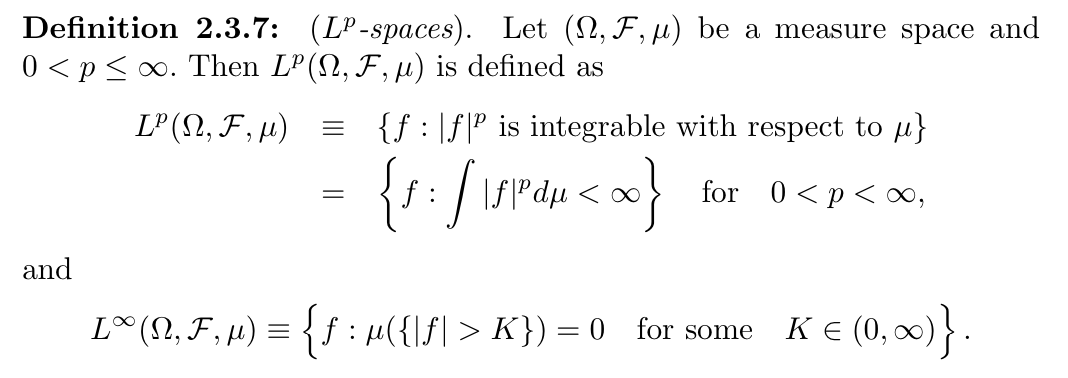
2. linear map

• Def: linear map

  

  2

  

  

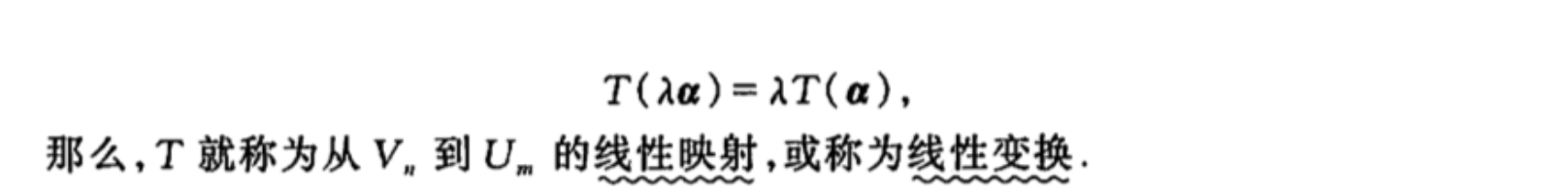
  • Qua: => qualities

    

    

  • Qua: => dimension

    

• Def: injective, （单射，两个变量不能得到同一个结果）

  

• Def: surjective ， （漫射，值域被完全覆盖）

  

• Def: orthotal map

  

2.1. null space & range

2.1.1. null space

• Def: null space

  

  • Qua: necc & suff

    

  • Qua: => subspace

    

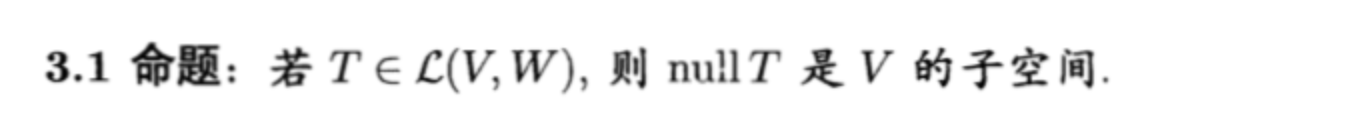
2.1.2. range space

• Def: range space

  

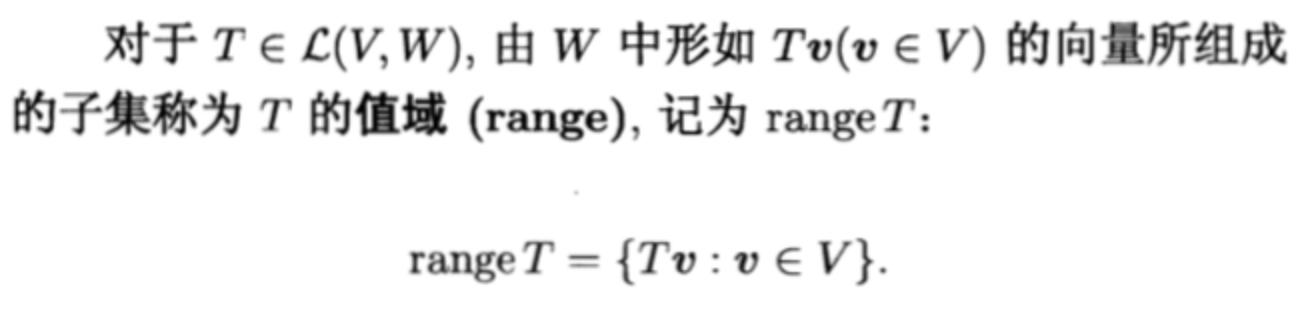
  • Qua: => subspace

    

2.2. matrix

2.2.1. matrix properties

2.2.1.1. basic

• Def: from V(n) -> W(m) = m x n

  

  

  

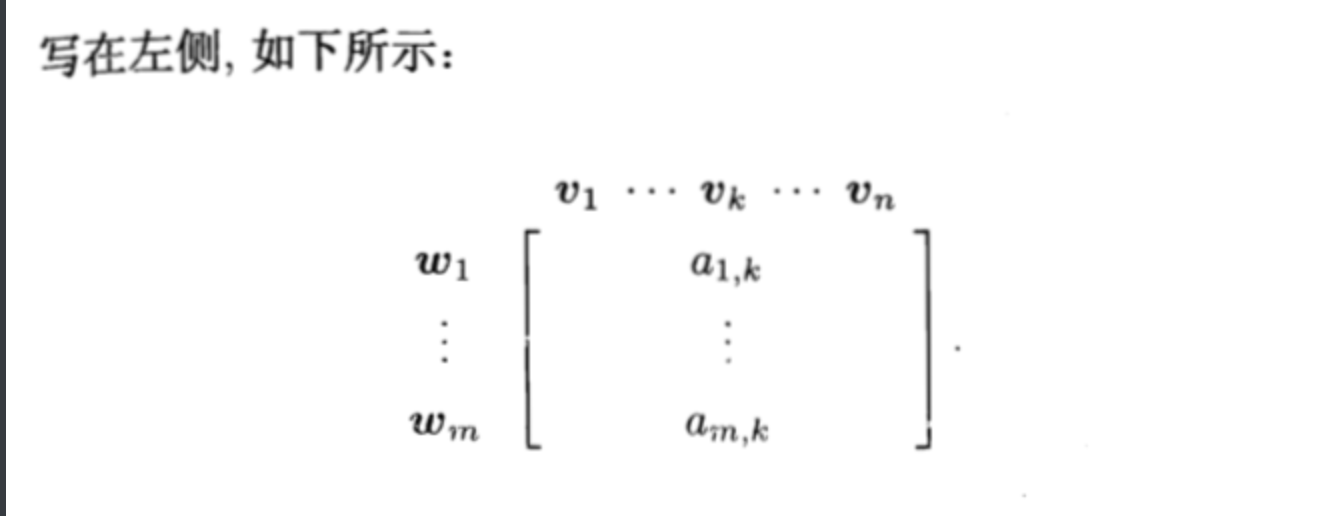
  • Def: matrix of particular vector （坐标）

    

  • Qua: 变基 =〉 基与基的关系

    

    

  • Qua: 变基 =》坐标与坐标的关系

    

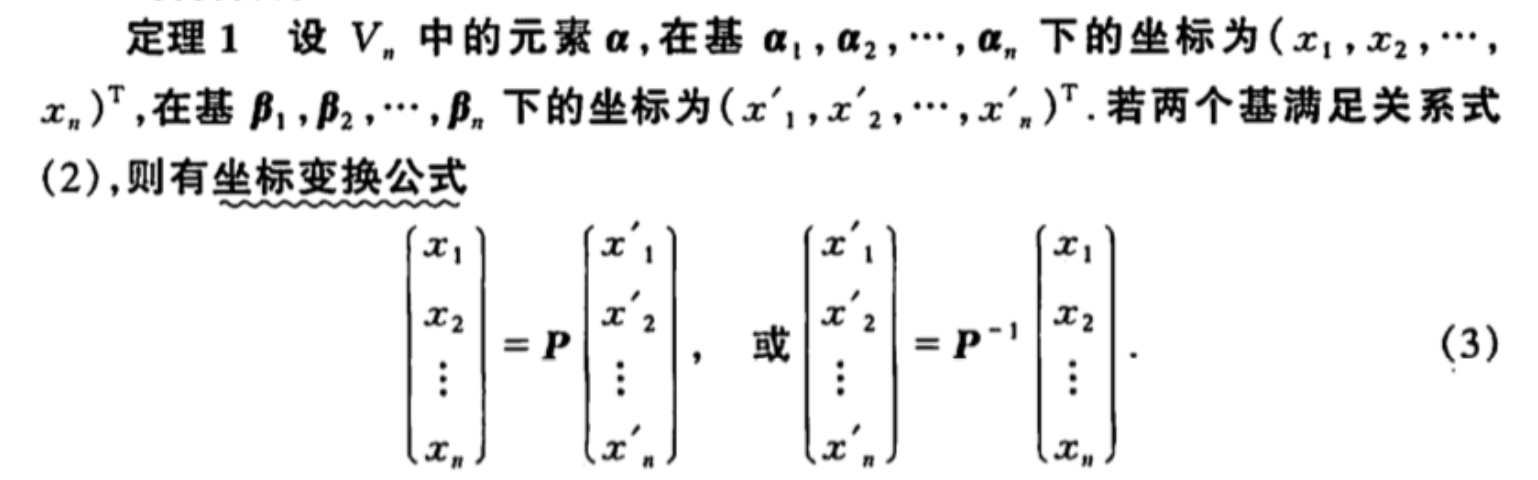
  • Theorm: 变换 =》 坐标与坐标的关系

    

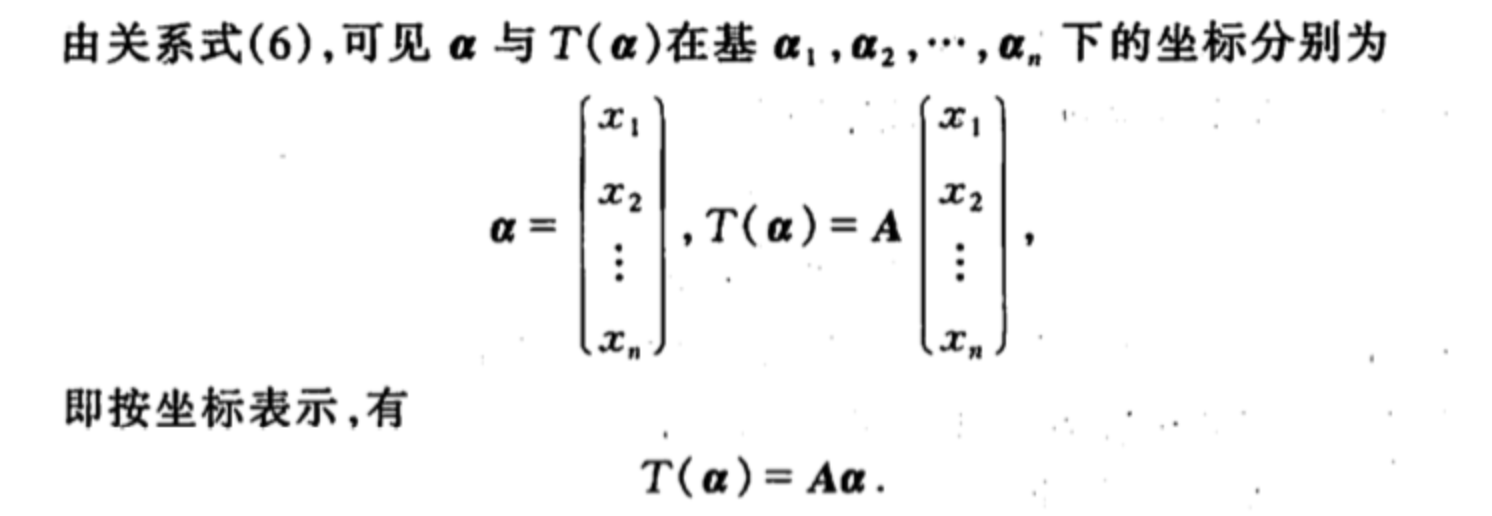
  • Theorm: 变换 + 换基 =》坐标与坐标的关系

    

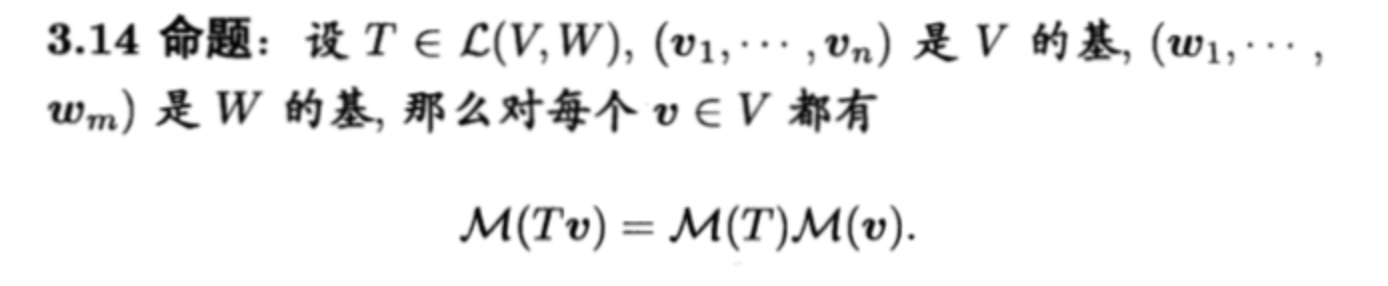
  • Qua: 变换+变基 =》 各种矩阵的关系

    

  • Qua: operation

    

    

    

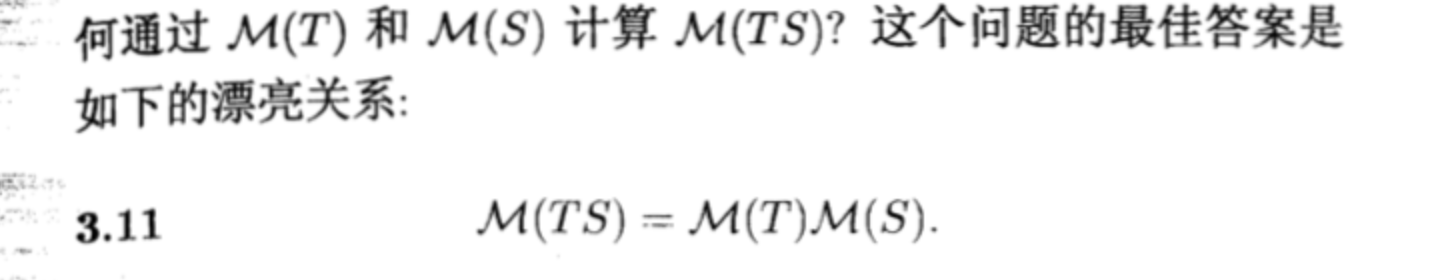
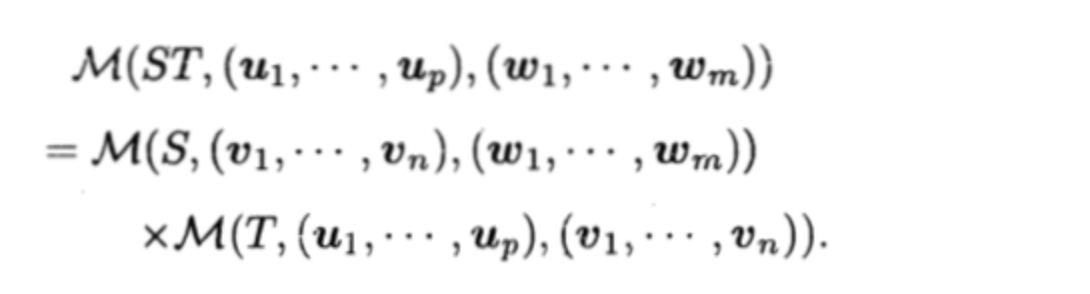
2.2.1.2. invertible

• Def: invertible

  

  • Qua: necc & suff

    

  • Qua: necc & suff

    

  • Qua: necc & suff

    

  • Qua: => only one

    

  • Qua: special =>

    

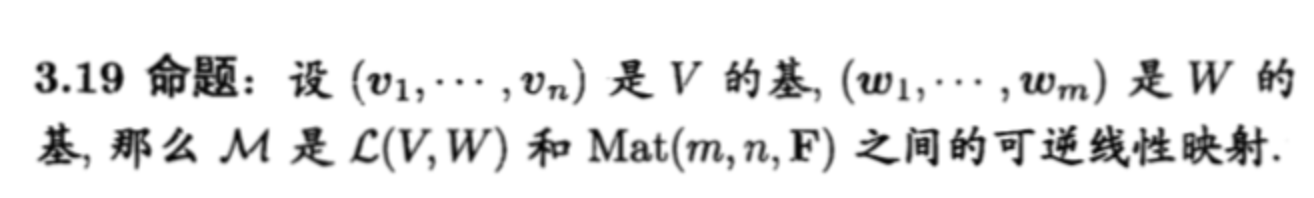
  • Def: isnorphic

    

    • Def: necc & suff

      

  • Qua: operation

    

    

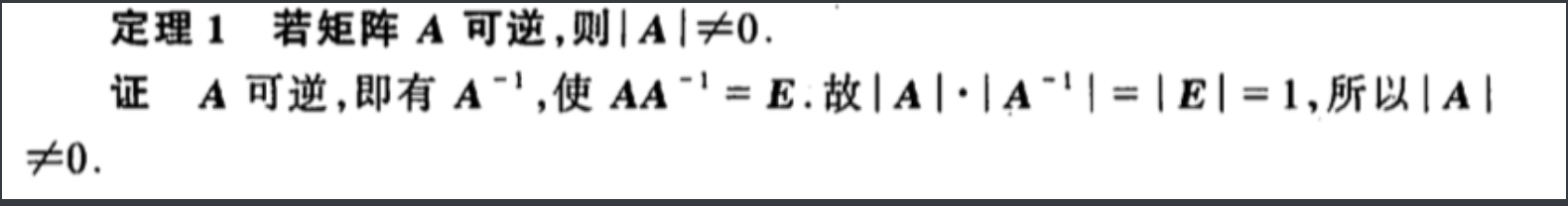
2.2.1.3. change of basis

• Theorm: change from u to v (with in V) =>

  

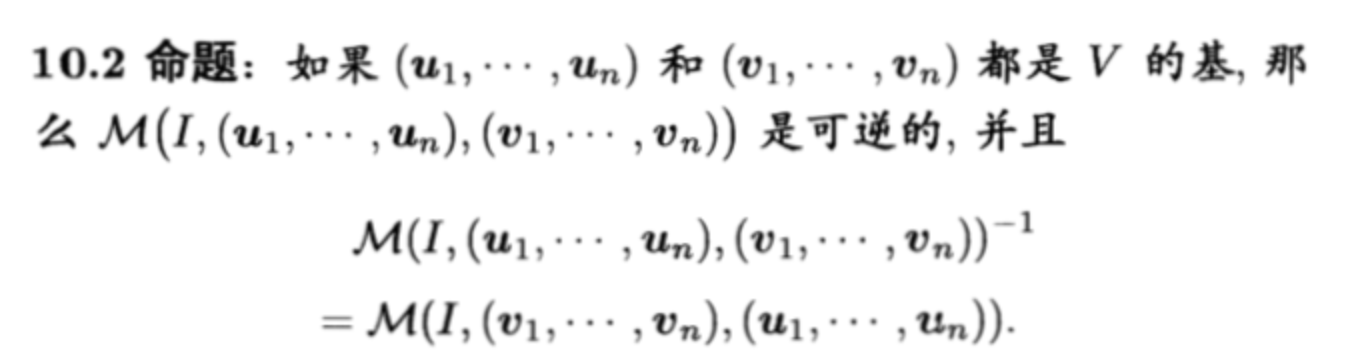
• Theorm: change from u to v (with in V)=>

  

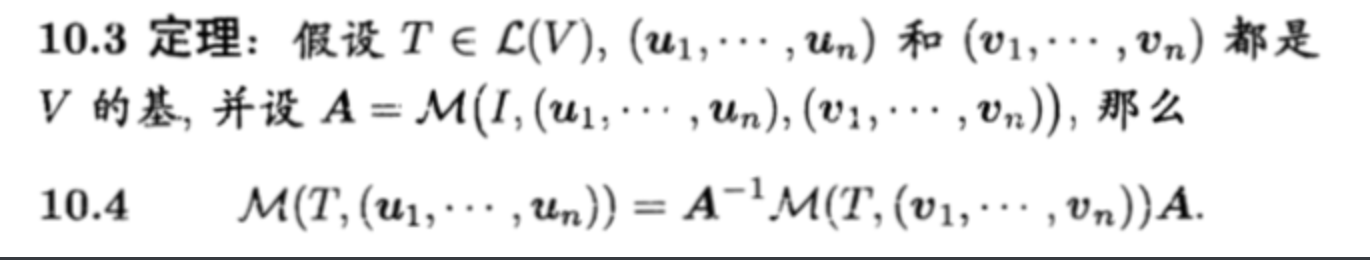
2.2.1.4. trace

• Def: trace of function

  

  • Qua: => sum of egvalue

    

  • Theorm: trace of function = trace of matrix

    

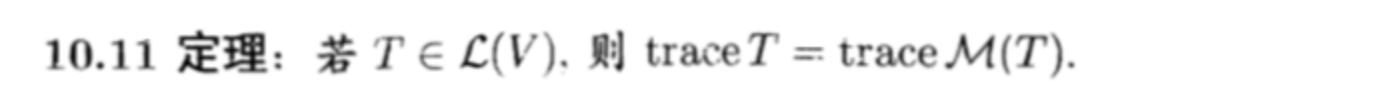
    • Corollary:

    

  • Qua: operation

    

    • Corollary:

      

2.2.1.5. determinant

• Def: d of function

  

  d of matrix

  

  • Qua: => inver

    

  • Qua: => same

    

  • Lemma:

    

  • Theorm: => p(T)

    

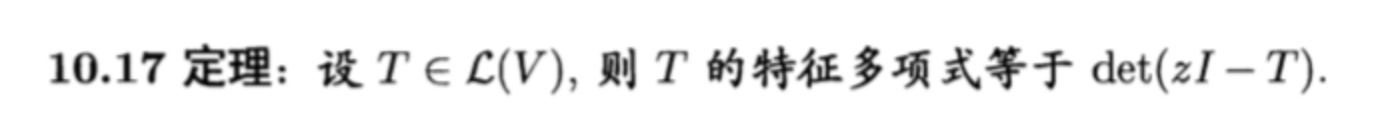
  • Theorm: Karamo => equation

    

    

    

    • Corollary

      

  • Qua: operation

    

    

    

    

    

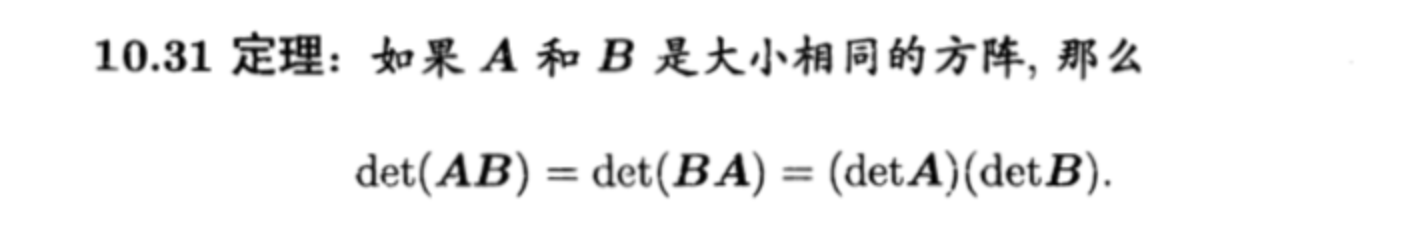
    • Corollary

      

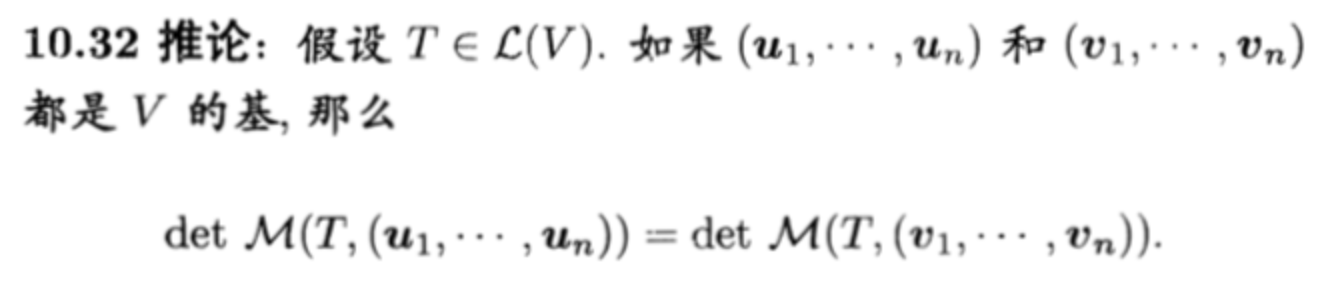
    • Corollary

      

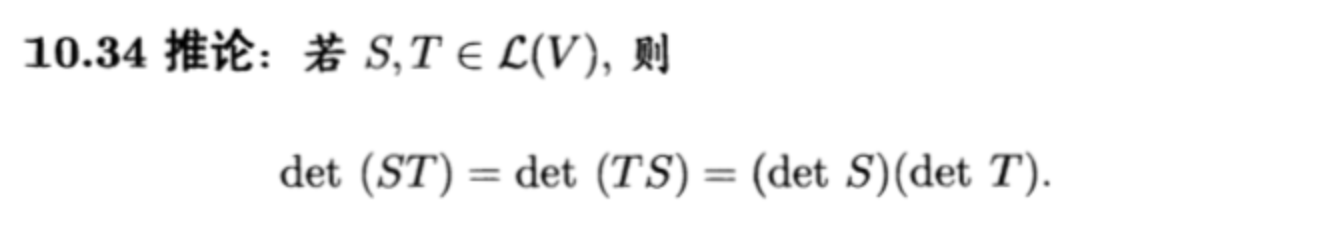
2.2.1.6. rank

• Def: k

  

• Def: rank

  

  • Theorm: rank = rank

    

  • Qua: => AX=0

    

  • Qua: => AX=bequatins

    

    

    

  • Qua: operations

    

2.2.2. relationships between matrix

2.2.2.1. equivalent

• Def: variations

  

• Def: equivalence

  

  • Qua: necc & suff

    

    • Corollary

      

  • Qua: => rank

    

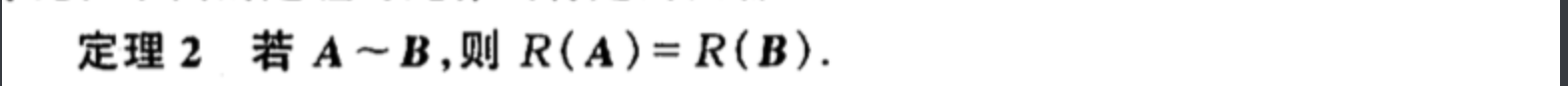
2.2.2.2. similar

• Def: similar

  

  • Theorm: necc & suff of similar to diag

    

  • Qua: => same egvalue

  

2.2.2.3. congruent

• Def: 二次型 & 标准型

  

  

  • Theorm: same way=>

    

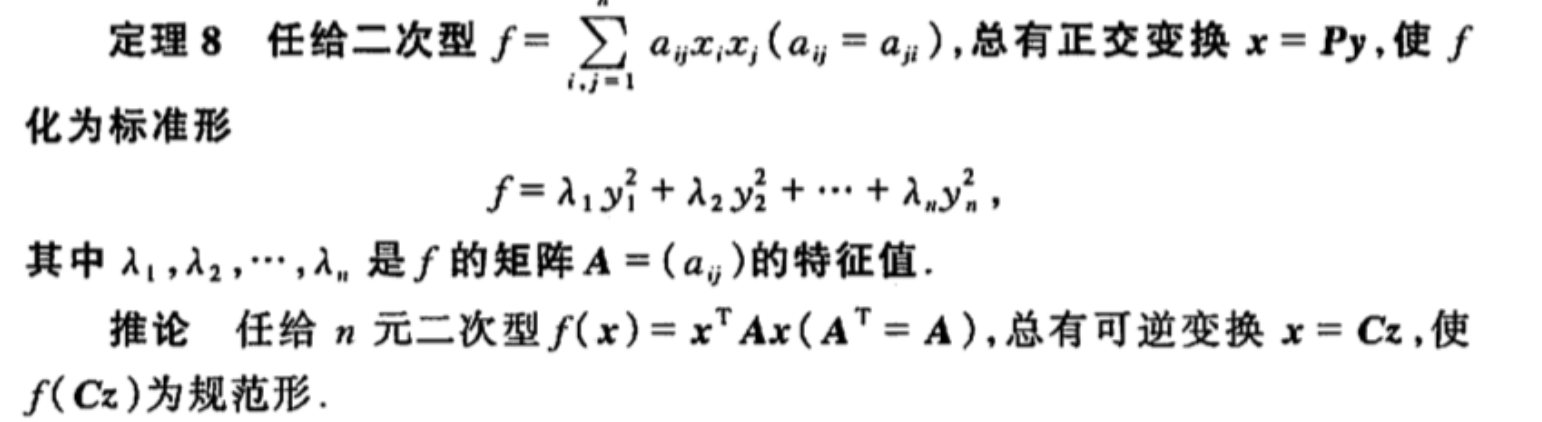
  • Theorm: => xxx

    

    

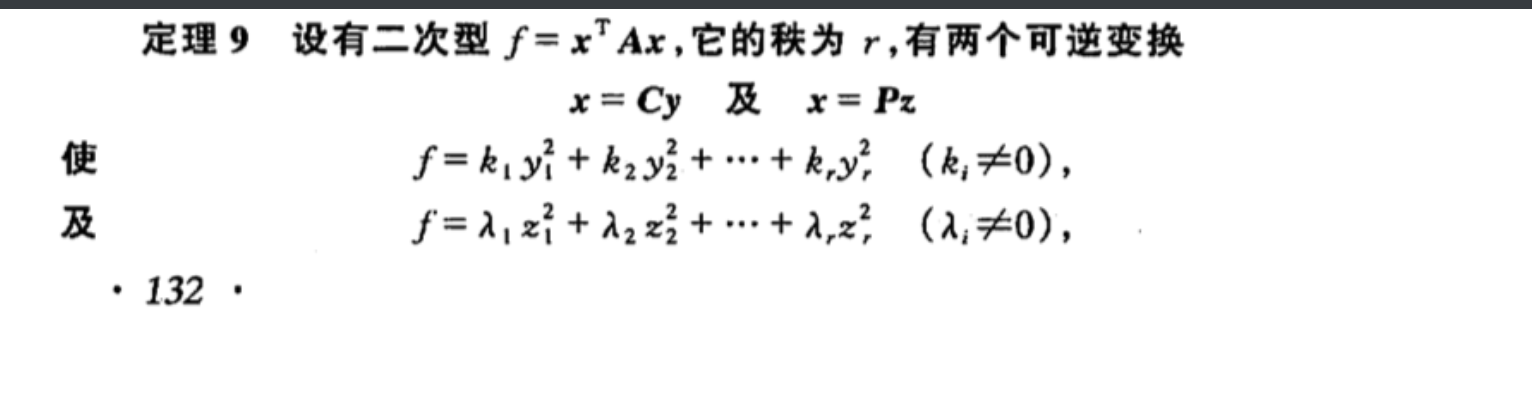
• Def: congruent

  

2.2.3. special matrix

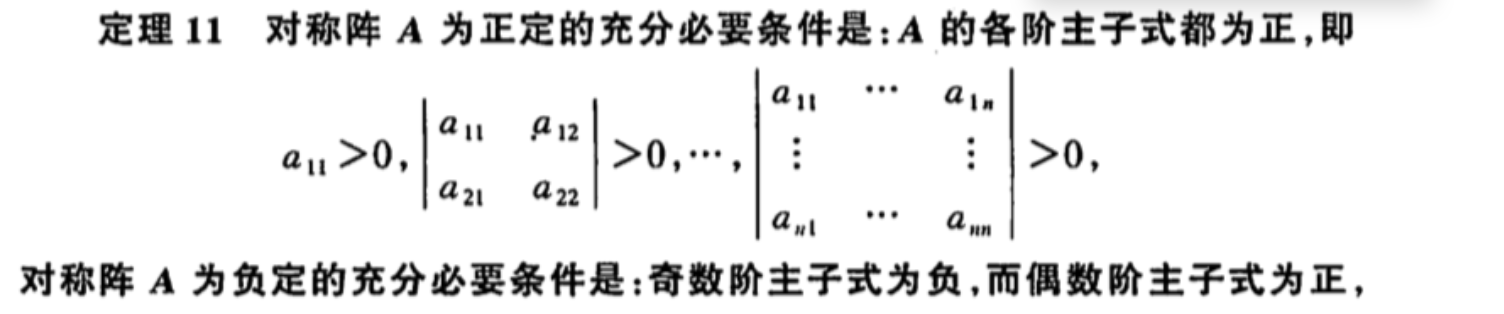
2.2.3.1. positive definite matrix

• Def: positive

  

  • Qua: necc & suff

    

    

    

2.2.3.2. orthogonal matrix

• Def: orthogonal matrix

  

  • Qua: necc & suff

    

    

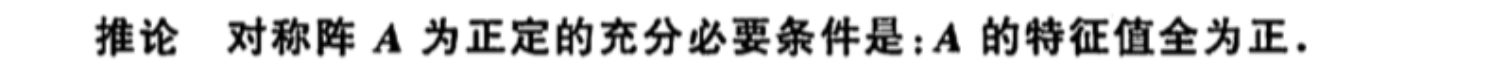
    (wiki)

    

  • Qua: =>

    

2.2.3.3. symmetric matrix

• Theorm: => egvalue

  

• Theorm: => ortho

  

• Theorm: => decomposition

  

  • Corollary

    

    Algorithm

    

2.3. eigenvalue

2.3.1. eigenvalue

• Def: invariant

  

• Def: eigenvalue (就是寻找1维不变子空间，一个子空间对应一个eigvector和valu

  

  • Qua: necc & suff

    

  • Qua: => same matrix and function

    

  • Qua: => independent

    

    

    • Corollary:

      

  • Qua: => every one has

    

  • Qua: operation

    

2.3.2. upper matrix

• Def:...

  • Theorm: necc & duff

    

  • Theorm: => inverisible

    

  • Theorm: => eigvalue

    

  • Theorm: => otho basis

    

  • Theorm: some basis =>

    

2.3.3. diagonal matrix

• Def:...

  • Qua: necc & suff

    

    

  • Qua: necc & suff

    

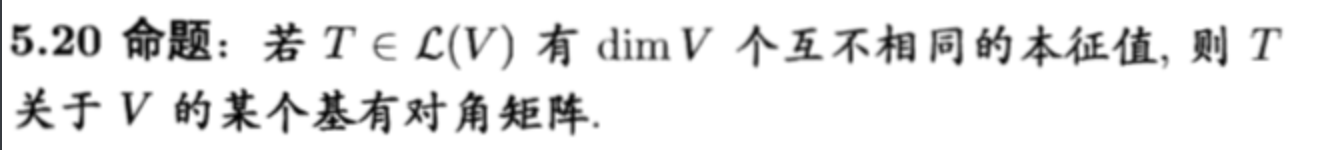
  • Qua: necc & suff

    

2.3.4. same egenvalue

2.3.4.1. generalized egvalue

• Def: generalized egvalue

  

• Theorm: about null space

  

• Theorm: about null space

  

  • Corollary : egvalue =>

    

• Theorm: about range space

  

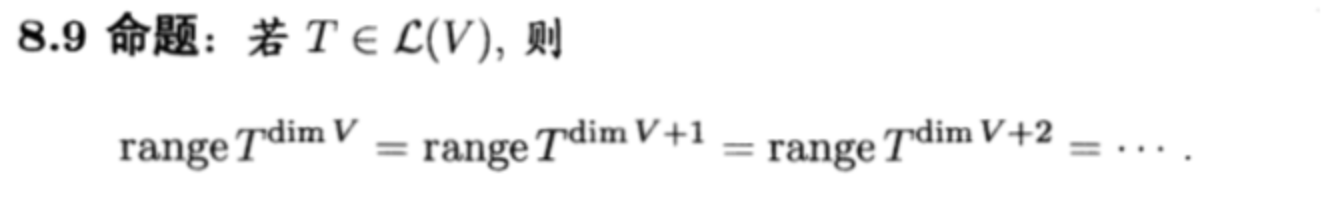
• Def: nilpotent

  

  • Qua: =>

    

2.3.4.2. characteristic polynomial

• Theorm: important!

  

• Def: multiplicity

  

  • Theorm: => sum

    

• Def: characteristic polynomial qt

  

  • Theorm: => qt= 0

    

2.3.4.3. decomposition

• Theorm:

  

• Theorm: princliple structure decomposition

  

  • Corollary:

    

• Lemma:

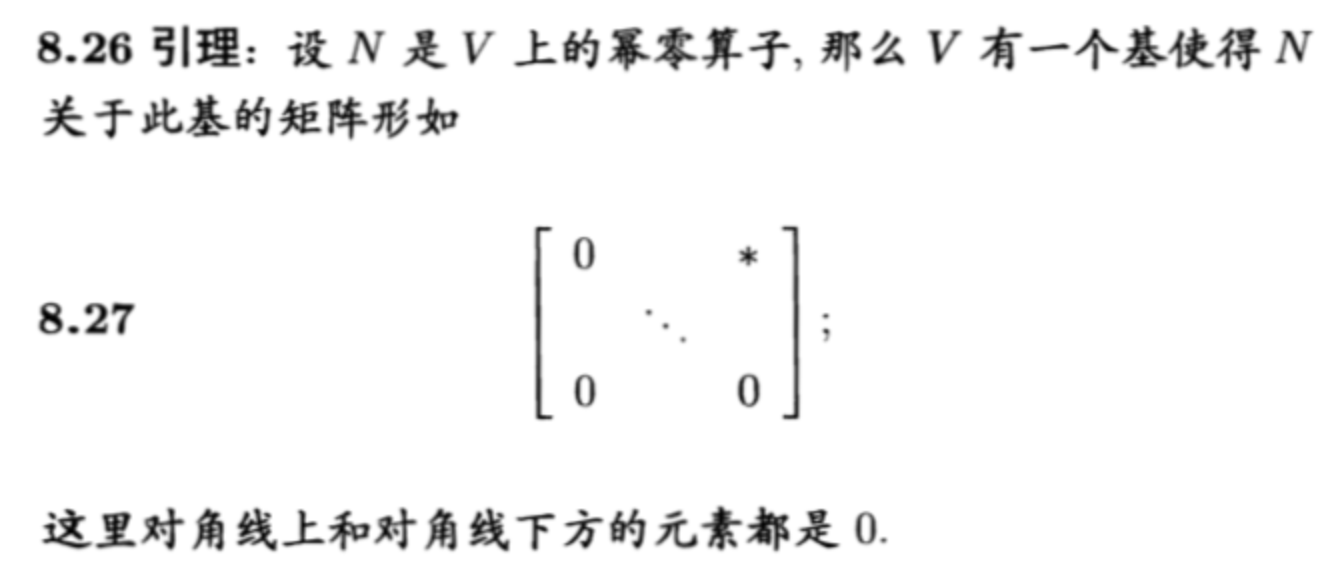
• Theorm: important

  

• square root ( application of 2.4.7.1)

• Lemma:

  

• Theorm: inver => square root

  

2.3.4.4. minimal polynomial

• Def:

  

  

• Theorm: => 包含q(T)

  

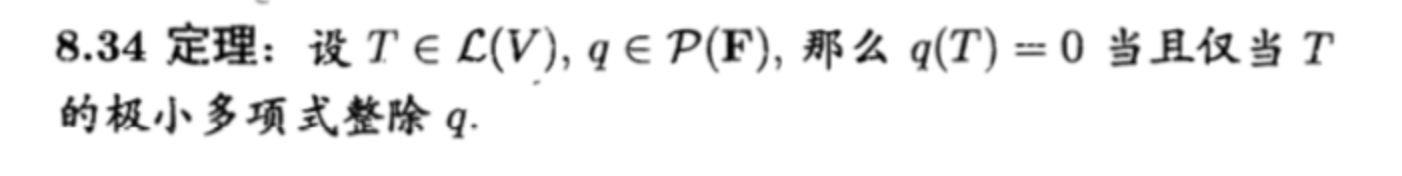
• Theorm: => egvalue （和特征多相似根相同，但是重数不同；特征多项式重根数对应特征值重数，极小多项式对应最大jordan块的介数）（所以我们可以认为一个特征值重数= 特征多项式重数 = jordan块 + jordan块 ，其中最大Jordan块介数 = 极小多项式重数）

  

  

2.3.4.5. jordan basis

• Lemma

  

• Def: jordan basis

  

  • Theorm: any =>

    

2.3.5. real vector space

2.3.5.1. basic

• Theorm:

  

• Theorm:

  

2.3.5.2. block upper matrix

• Def:

  • Theorm:

    

2.3.5.3. pt

• Theorm:

  

  

• Def: multiplicity

  

  • Theorm:

    

2.3.6. eigen decomposition (web)

• Def: eigen decomposition

  

  x1, x2 are orthogonal

  

  decomposition, no proof

  

3. polynomial

• Def: 多项式

  

3.1. root

• Def: 次数

  

• Def: root

  

  • Qua: necc & suff

    

  • Qua: => number of roots

    

    • Corollary:

      

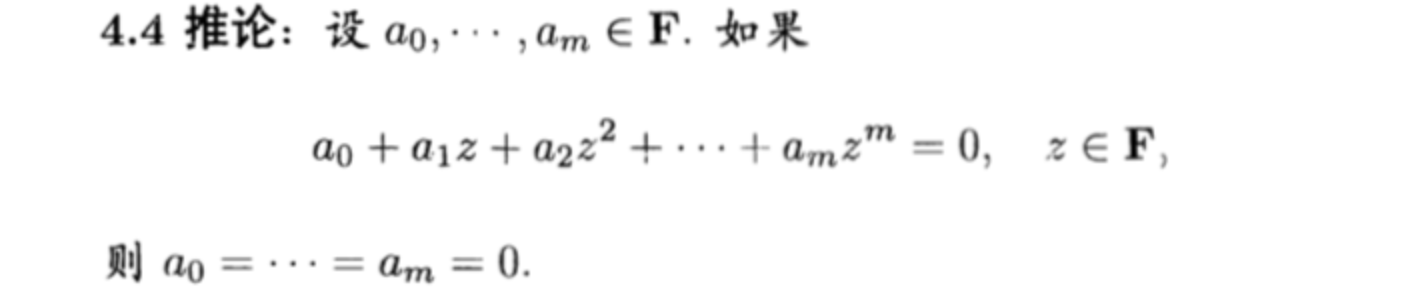
• Theorm: division algorithm

  

3.2. complex coefficient

• Theorm: fundamental theorm of algebra

  

  • Corollary:

    

3.3. real coefficient

• Theorm: => root

  

• Lemma: to prove the below

  

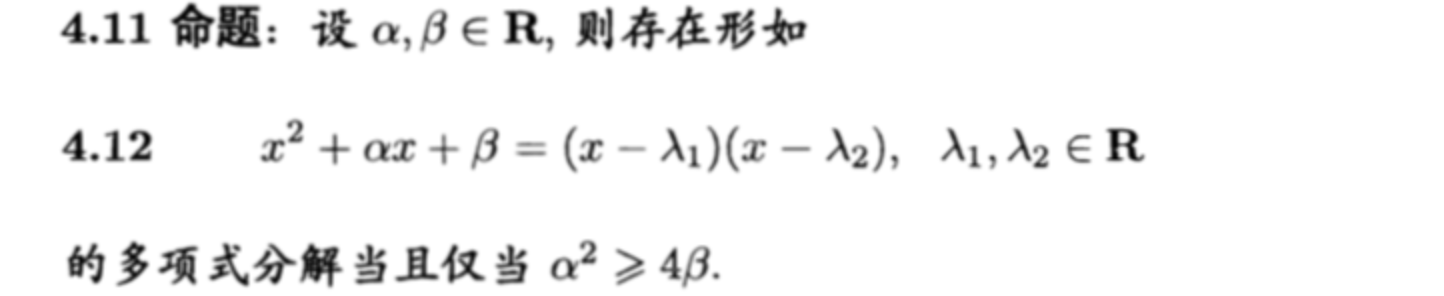
• Theorm: 分解定理

  

3.4. multi linear function

• Def: 多项式算子