Convex Optimization Course Slides Notes
1. convex set
1.1. classes of convex set
Def: convex set

Example:

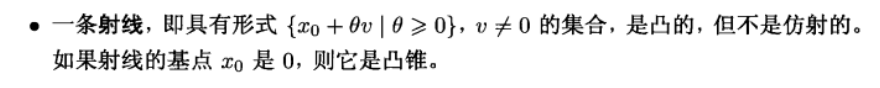
Def: conv

1.1.1. affine set
Def: affine set (lines)

Note: dim > 1

Note: other def

Example:


Def: aff

Def: aff dim

Def: relint and cl

1.1.2. convex hull
Def: convex hull

Example:

1.1.2.1. norm hull
Def:

1.1.3. hyperplane
Def: hyperplane

1.1.3.1. positive hull
Def:


1.1.4. half space
Def:


1.1.5. Euclid ball
Def:

1.1.6. ellipsoid
Def:

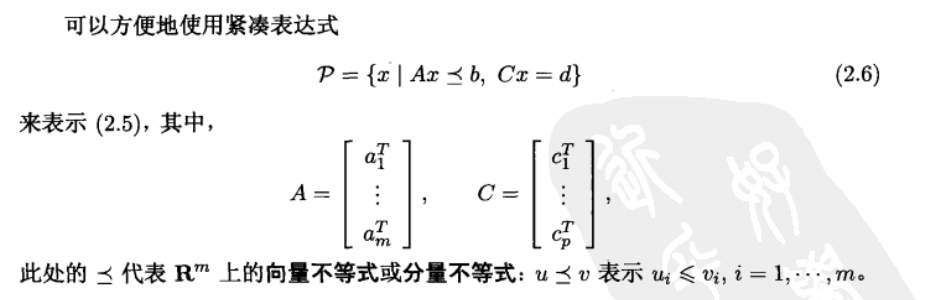
1.1.7. polyhedral
Def:

Note:
1.1.7.1. singleton
Def:

1.2. convex operations
1.2.1. intersection
Def:

1.2.2. affine functions
Def:

Example:

Example:
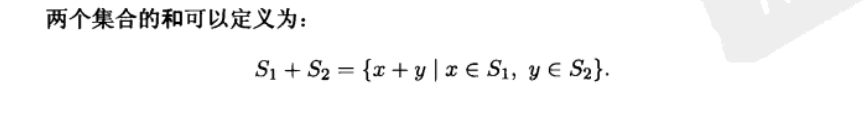

Example:

1.2.3. perspective function
Def:

Note:

Note:

1.2.4. linear
Def:

Note:

2. convex function
Def:

Example:

Example:

Example:
P67
Qua: necc & suff

first condition
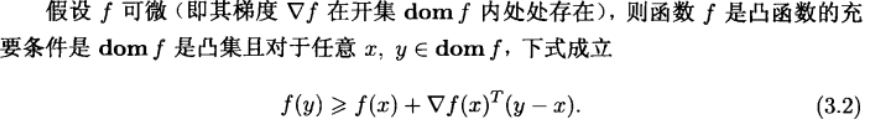

Note: first condition

second condition

2.1. induced sets
2.1.1. sublevel set
Def:

Qua: => convex


2.1.2. epigraph
Def:
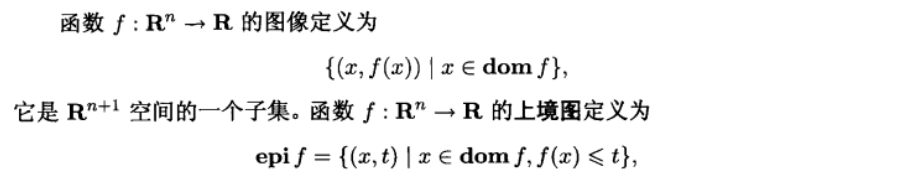
Qua: necc & suff

2.2. induced functions
2.2.1. conjugate function
Def:

Qua: convex

Qua:

Qua:

Qua: =>

Qua:

Qua:

2.3. convex operations
2.3.1. sum of positive weight
- Def:

2.3.2. affine function
Def:

2.3.3. point-wise max
Def:


Note: generalization

2.3.4. combinations
Def:
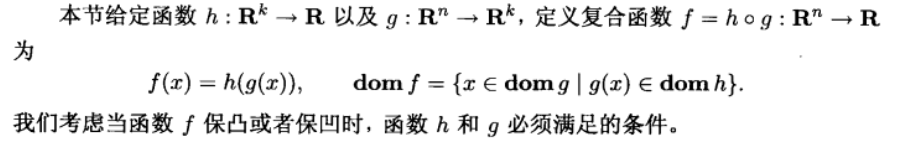
see p81
2.3.5. min
Def:

2.3.6. projection
Def:

3. convex problem
4. convex solving
4.1. =+>
4.1.1. KKT
4.1.2. Barrier Method
4.1.3. Primal Dual method
4.1.4. Linear Programming
##=
4.1.5. problem attributes
4.1.6. newton descent
4.1.7. improved newton
4.2. no constraint
4.2.1. problem attributes
4.2.2. general descent
4.2.3. gradient descent
4.2.4. steepest descent
###newton descent

